P5676 [GZOI2017]小z玩游戏 Tarjan+优化建图

题目描述

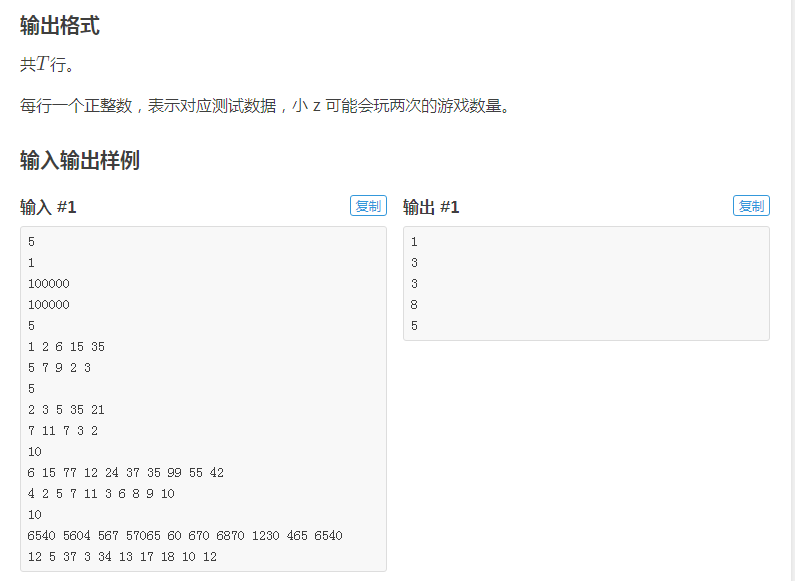
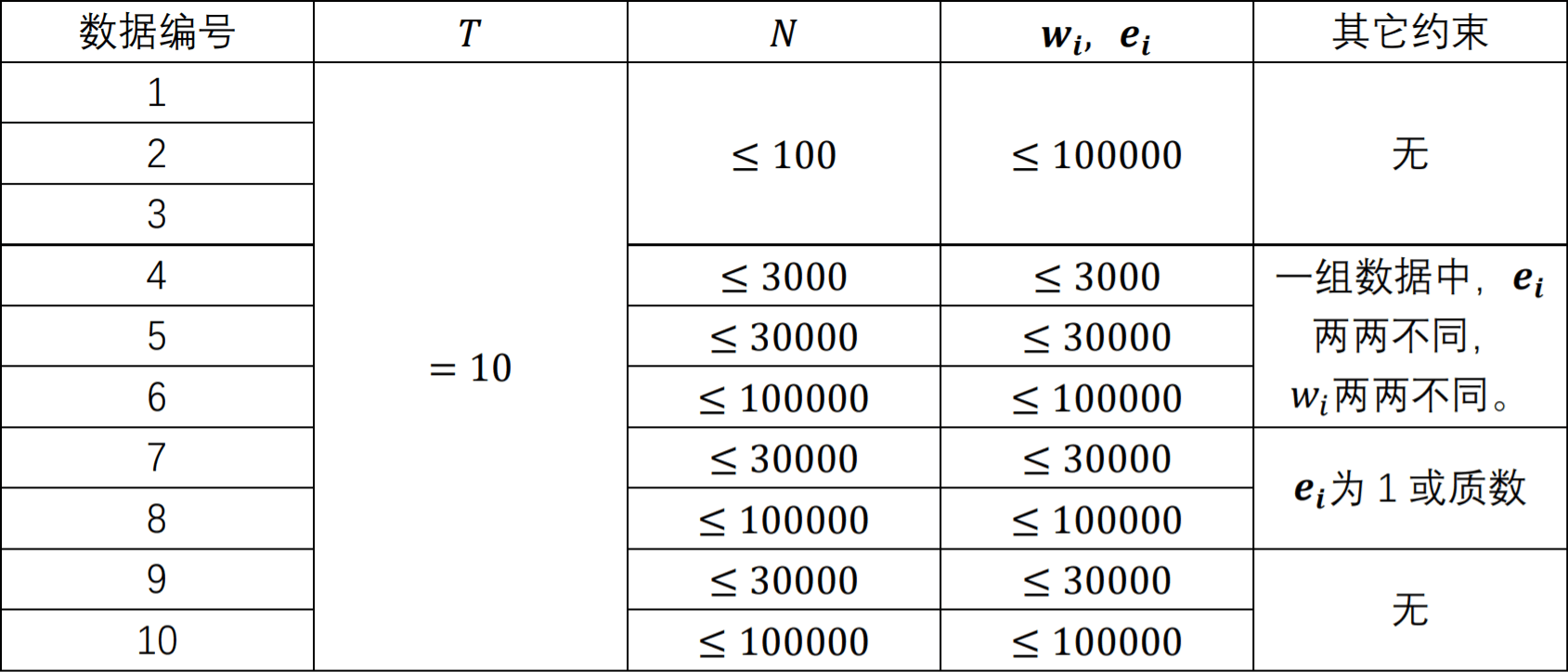
分析

一开始看到这道题，首先想到的就是建好边后跑一个Tarjan缩点，将siz大于1的节点统计一下，输出结果

Tarjan非常显然易得，关键就是怎么建边

比较好想的一种思路就是枚举每一个兴奋程度

对于每一个兴奋程度，再将有趣程度枚举一遍

如果有趣程度是兴奋程度的倍数的话，在两个节点之间建一条有向边

我们拿第二个样例模拟一下，建好边后就是下面这样



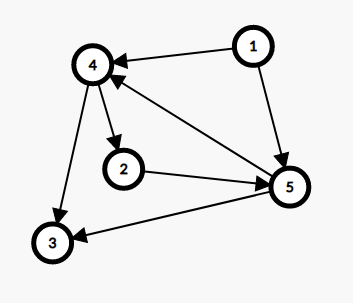
那么缩点后大小不为1的强连通分量只有一个，它的大小为3

那么最终的答案就是\(3\)

但是这样的建边效率为\(n^2\)，复杂度接受不了

所以我们考虑更优秀的建边方法

这里要用到的是建虚点的方法

1.建一个由 有趣程度 到 点 的边

2.建一个由 点 到 兴奋程度 的边

3.重点：建一个兴奋程度整数倍的边

要注意的是建虚点的时候，要把游戏的编号加上一个\(n\)

避免和原先的编号重复

然后思路就和\(n^2\)的解法一样

至于时间复杂度，根据大佬的证明，是

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+5;
struct asd{
    int from,to,next;
}b[maxn];
int head[maxn],tot=1;
void ad(int aa,int bb){
    b[tot].from=aa;
    b[tot].to=bb;
    b[tot].next=head[aa];
    head[aa]=tot++;
}
int dfn[maxn],low[maxn],top,sta[maxn],dfnc,shuyu[maxn],siz[maxn],js,vis[maxn];
void tar(int xx){
    dfn[xx]=low[xx]=++dfnc;
    sta[++top]=xx;
    for(int i=head[xx];i!=-1;i=b[i].next){
        int u=b[i].to;
        if(!dfn[u]){
            tar(u);
            low[xx]=min(low[xx],low[u]);
        } else if(!shuyu[u]){
            low[xx]=min(low[xx],dfn[u]);
        }
    }
    if(low[xx]==dfn[xx]){
        js++;
        siz[js]=1;
        while(sta[top]!=xx){
            int now=sta[top--];
            shuyu[now]=js;
            siz[js]++;
            vis[now]=1;
        }
        top--;
        shuyu[xx]=js;
        if(siz[js]>1) vis[xx]=1;
    }
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        memset(head,-1,sizeof(head));
        memset(&b,0,sizeof(struct asd));
        memset(dfn,0,sizeof(dfn));
        memset(low,0,sizeof(low));
        tot=1,js=0,dfnc=0,top=0;
        memset(vis,0,sizeof(vis));
        memset(sta,0,sizeof(sta));
        memset(shuyu,0,sizeof(shuyu));
        memset(siz,0,sizeof(siz));
        int n;
        scanf("%d",&n);
        int mmax=0;
        for(int i=1;i<=n;i++){
            int aa;
            scanf("%d",&aa);
            ad(n+aa,i);
            mmax=max(mmax,aa);
        }
        for(int i=1;i<=n;i++){
            int aa;
            scanf("%d",&aa);
            ad(i,n+aa);
        }
        for(int i=1;i<=mmax;i++){
            for(int j=2;j*i<=mmax;j++){
                ad(n+i,n+i*j);
            }
        }
        for(int i=1;i<=n;i++){
            if(!dfn[i]) tar(i);
        }
        int ans=0;
        for(int i=1;i<=n;i++){
            if(vis[i]==1) ans++;
        }
        printf("%d\n",ans);
    }
    return 0;
}