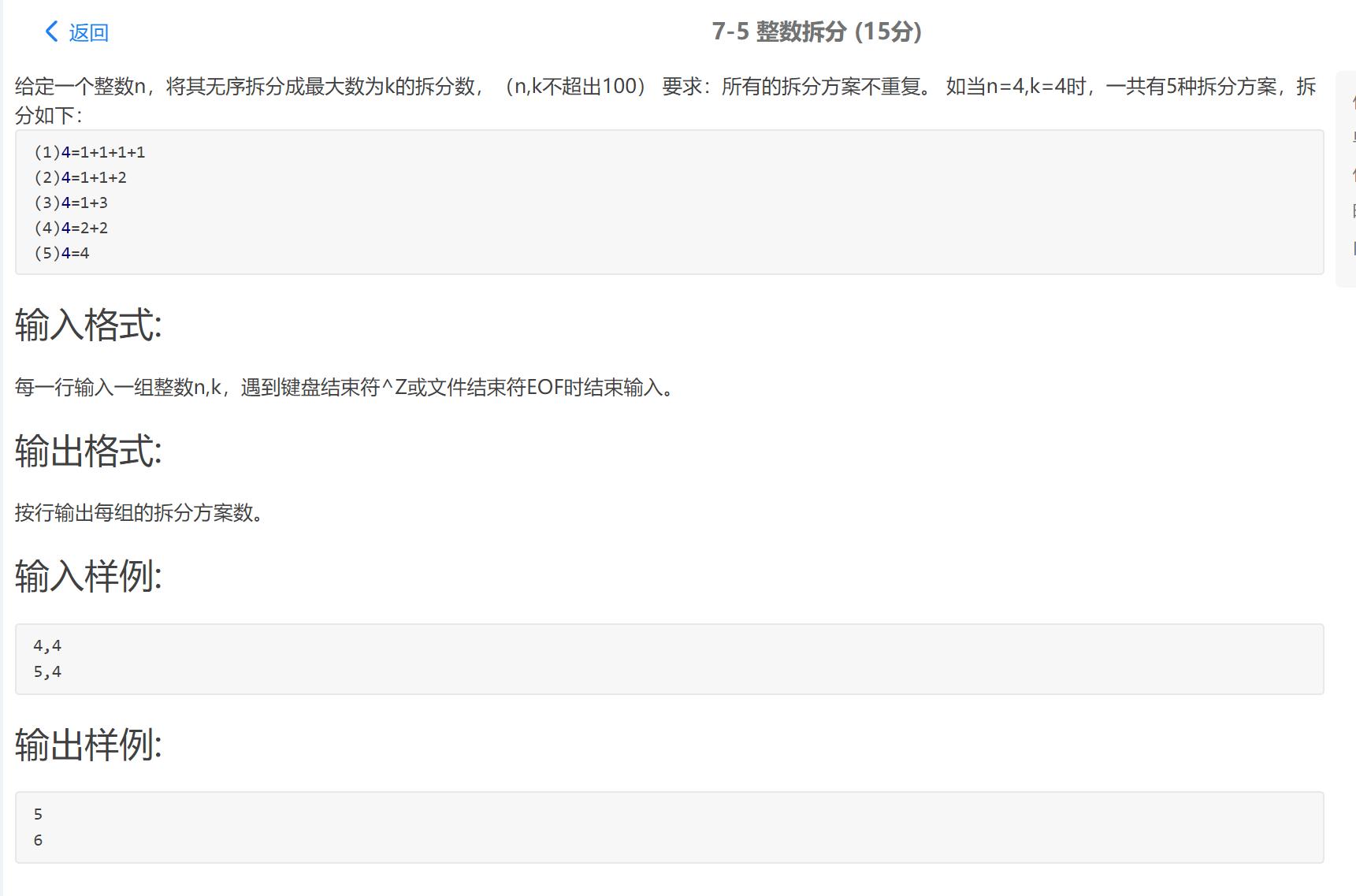
整数划分(硬币问题)(dp)

题目描述

考试时思路

本菜狗考试的时候，第一扁打了纯dfs，15分拿了9分

后面看了时限400ms，多组数据，以为会卡常数，然后就想着先dp打表然后再直接O(1)查询

后面发现自己想多了，数据有点水……dfs+dp都可以过

然后打表，找规律找到了后半段$[\cfrac{i}{2}+1,i]的规律

for(int j=(i>>1)+1;j<=i;j++)dp[i][j]=dp[i][j-1]+dp[i-j][i-j];

没有联想到第一段的规律，归根到底还是自己dp太弱了

正解思路

dp[i][j]表示，n=i,j=k时候，总的划分方案数

当j>i时候，就例如数只有4，上限却是5，所以dp[i][j]可以用dp[i][i]表示

i划分为最大为j的若干个数，分两种情况

一种情况就是里面有j,1*dp[i-j][j]

另一种就是里面没有j,dp[i][j-1]

所以最后的状态转移方程为dp[i][j]=dp[i][j-1]+dp[i-j][j]

代码实现

#include<bits/stdc++.h>
using namespace std;
int dp[102][102],n,k;
int main(){
	for(int i=0;i<=100;i++)dp[0][i]=dp[i][1]=1;
	for(int i=2;i<=100;i++){
		for(int j=2;j<=i>>1;j++)dp[i][j]=dp[i][j-1]+dp[i-j][j];
		for(int j=(i>>1)+1;j<=i;j++)dp[i][j]=dp[i][j-1]+dp[i-j][i-j];
	}
	while(~scanf("%d,%d",&n,&k))printf("%d\n",dp[n][k]);
}