IEEE754二进制浮点数算术标准

对于32位浮点数

sign: 符号，1位

exponent: 指数，8位，偏码

fraction: 分数，23位，原码

特殊值

 

指数域的编码值 = 指数的实际值 + 127

这样按照字典序的顺序就可以比较两个指数域的编码值的大小，在比较两个浮点数大小时比使用原码方便

规约形式

“规约”是指用唯一确定的浮点形式去表示一个值。

即要求fraction部分最高有效位为1，且指数域的编码值不为0

由于这种表示下的尾数有一位隐含的二进制有效数字（因为最高位总是1，所以按照规约数解析时，自动在最前面添加1，这个1是不存储在bit中的，非规约数不会自动添加1），为了与二进制科学计数法的尾数（mantissa）相区别，IEEE754称之为有效数（significant）。

IEEE754要求

exponent编码值为全0，fraction部分存储的编码值不为全0时，按照非规约数解析，此时实际指数看作-126而不是-127

exponent为1~2^e-1，-2^e-2~-1，按照规约数解析

非规约形式

exponent为0，fraction不为0，之所以同时存在非规约形式，是因为绝对值最小的规约浮点数为1.0*2^-126，绝对值次小的规约浮点数为（1+2^-23）*2^-126，两者距离2^-149，而绝对值最小的规约浮点数于0的距离是2^-126，可以看出，两个绝对值很小的规约浮点数之间的距离比它们到0的距离近很多，这样导致两个不等的很小的规约浮点数的差变成0，这种方式称作突然式下溢出（abrupt underflow）。而渐进式下溢出（gradual underflow）因为引入非规约浮点数，最小的非规约浮点数的绝对值为2^-23*2^-126，次小的为2^-22*2^-126，两者距离2^-149，同时，最小的非规约浮点数与0之间的距离也是2^-149。

浮点数举例

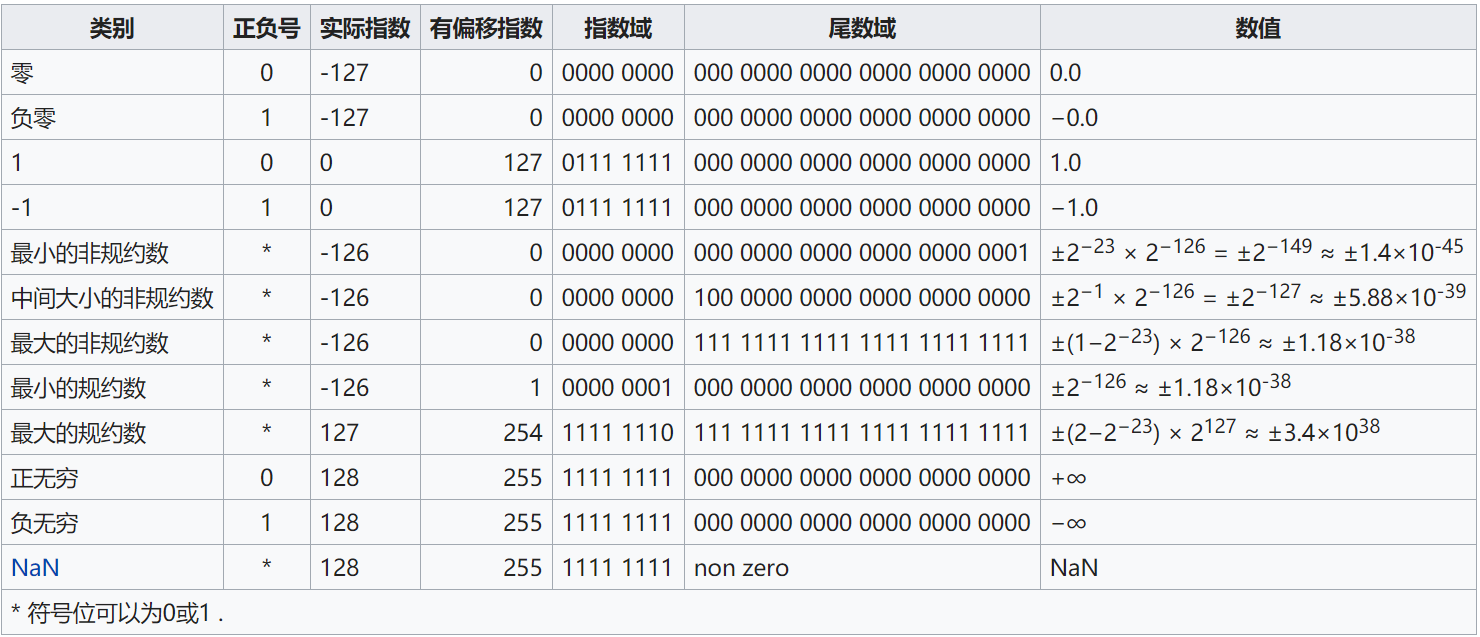
参考文献：https://zh.wikipedia.org/wiki/IEEE_754