python实现斐波那契数列

https://www.cnblogs.com/wolfshining/p/7662453.html

斐波那契数列即著名的兔子数列：1、1、2、3、5、8、13、21、34、……

数列特点：该数列从第三项开始，每个数的值为其前两个数之和，用python实现起来很简单：

a=0
b=1
while b < 1000:
    print(b)
    a, b = b, a+b

输出结果：

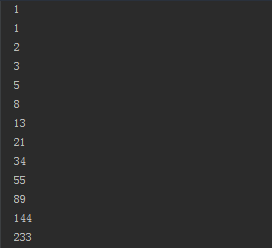
这里 a, b = b, a+b 右边的表达式会在赋值变动之前执行，即先执行右边，比如第一次循环得到b-->1,a+b --> 0+1 然后再执行赋值 a,b =1,0+1,所以执行完这条后a=1,b=1

a=0
b=1
while b < 1000:
    print(b,end=',')#end 可以将print输出到同一行并以 ,号结尾
    a, b = b, a+b

输出结果：

递归方式实现斐波那契数列 前n项:

# 递归方式实现 生成前20项
lis =[]
for i in range(20):
    if i ==0 or i ==1:#第1,2项 都为1
        lis.append(1)
    else:
        lis.append(lis[i-2]+lis[i-1])#从第3项开始每项值为前两项值之和

print(lis)

运行结果