Matlab:拟合(1)

拟合练习:

 function f = curvefun(x, tdata)
 f = (x()*x()*x()) / (x()-x()) * ( exp(-x()*tdata)/(x()-x()) + exp(-x()*tdata)/(x()-x()) - (/(x()-x())+/(x()-x()))*exp(-x()*tdata) );

 %数据输入
 tdata = [0.25 0.5 0.75  1.5  2.5  3.5  4.5            ];
 vdata = [                      ];
 %拟定估计值
 x0 = [   ];
 x = lsqcurvefit('curvefun', x0, tdata, vdata)
 f = curvefun(x, tdata)
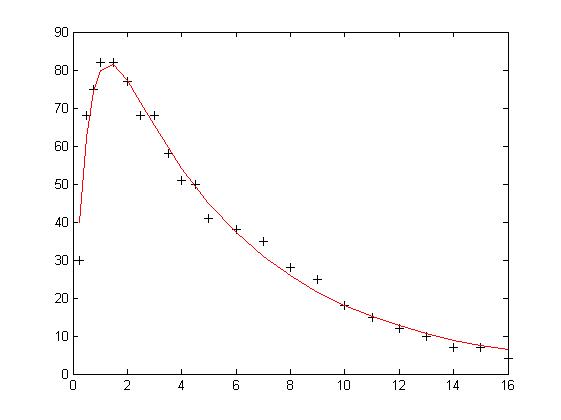
 %作散点图和你和图
 plot(tdata, vdata, 'k+')
 hold on
 plot(tdata, f, 'r')

结果: x =

256.2035    0.1512    0.2422    1.9506

f =

Columns 1 through 8

39.7501   62.2565   74.2700   79.9309   81.3616   77.1765   71.3312   65.2712

Columns 9 through 16

59.5001   54.1706   49.3072   44.8893   37.2494   30.9669   25.7925   21.5224

Columns 17 through 23

17.9914   15.0658   12.6370   10.6167    8.9330    7.5272    6.3515

方法一：解超定方程组

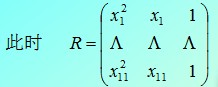
 x = :0.1:;
 y = [-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
 R = [(x.^)', x', ones(, )];
 A = R\y'

结果：
A =

-9.8108    20.1293    -0.0317

即为系数a1, a2, a3

方法二：用多项式拟合

 x = :0.1:;
 y = [-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
 %二次多项式拟合
 A = polyfit(x, y, )
 %计算拟合之后的原始数据点的函数值
 Y = polyval(A, x);
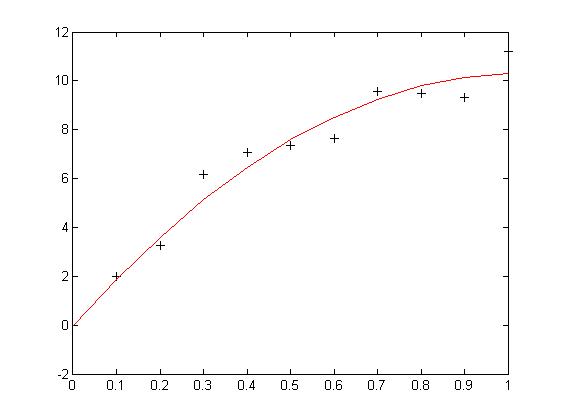
 %作出数据点和拟合曲线的图形
 plot(x, y, 'k+')
 hold on
 plot(x, Y, 'r')

结果：
A =

-9.8108   20.1293   -0.0317

拟合曲线