KMP模板及总结

KMP是一种字符串匹配算法，它在时间复杂度上较暴力匹配算法由很大的优势。比如我要找字符串S中是否存在子串P，如果暴力匹配的话，则时间复杂度为O（n*m），而kmp算法时间复杂度为O（n+m）。

这里我们有一个辅助的数组next[]（先别管怎么求出来的），next[i]含义是模式串P中[0....i-1]这一段的长度小于这段字符串的长度的最长公共前缀(比如ababa，公共前缀就是aba)。

好，那我们接下来讲一下kmp算法的具体操作：

假设，我们开始有字符串S：ababaaba   模式串P：abaa

对应next[i](0=<i<=len(P))的值为：

next[0]=-1 (无)

next[1]=0  (a)

next[2]=0  (ab)

next[3]=1  (aba)

next[4]=1  (abaa)

好，有了next数组，我们接下来进行匹配，设i=0是S上的当前匹配位置，j=0是P上的当前匹配位置。

第一次匹配，一直到i=3，j=3时匹配失败，令j=nxet[j]继续匹配。（为什么可以令j=next[j]？简单来说P[0...0]等于P[2...2]，而通过第一次匹配，我们知道P[2..2]等于S[2...2]，所以可以跳过这一段不用重复匹配，具体原理接下来解释）

第二次匹配，从i=3,j=1开始，匹配成功，获得答案。

大概过程就是这样。

下面按我自己的理解，解释一下kmp的原理：

如下图所示（图很丑，我真的不知道怎么画图），S[0...i]和P[0...i]匹配上了，匹配到i+1时匹配失败。

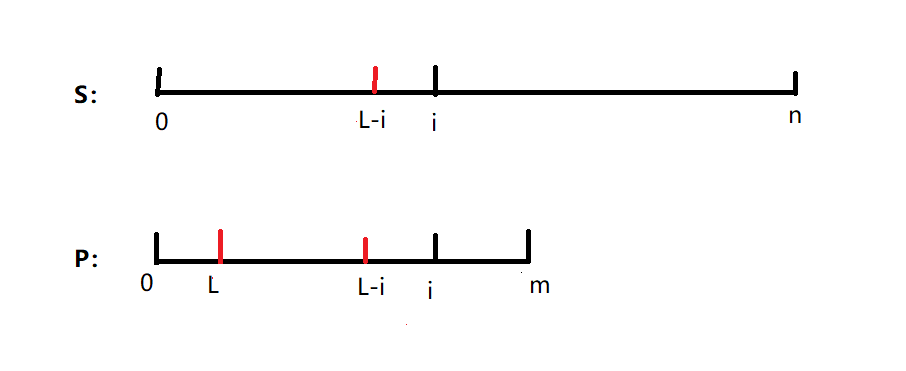
好，我们仔细分析一下，设L=nxet[i+1]，则P[0...L]等于P[i-L...i]，又因为通过刚才的匹配，我们确定了S[0...i]等于P[0...i]，所以在S上也有一段对应的S[L-i...i]=P[L-i..i]=P[0...L]。

所以第二次匹配时，我们可以直接将P挪动，使P[0...L]对应S[L-i...i]，直接从i+1开始匹配(即上文中的j=next[j])，如下图所示:

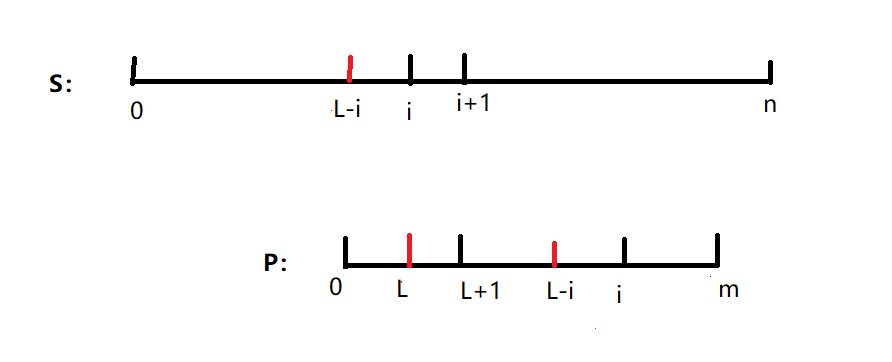
P[0...L]=S[L-i..i]可以理解，但是为什么可以直接挪过来呢，忽略了可能出现的情况怎么办？比如说下图这样的情况：

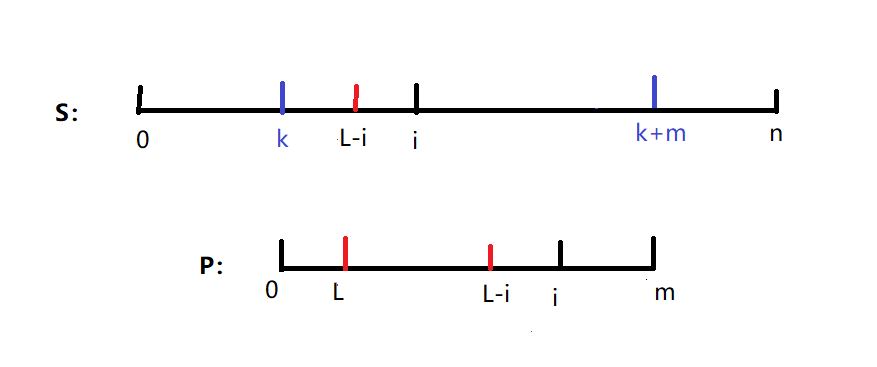
是否会有一段这样的字符串S[k..k+m]被我们忽略呢？若有的话，那显然k的位置更优因为i-k>L更有利于我们减少重复匹配。

实际上是不存在的，很容易知道，若存在一段长度大于L的S[k...i]=P[0...i-k+1]那么因为P[0...i]=S[0...i]肯定会有一段P[k..i]=S[k..i]=P[0..i-k+1]，即P[0...i-k+1]和P[k..i]是一段公共前缀。

但是前面我们说了L=next[i+1]表示P[0...i]的最长公共前后缀，而上述的情况存在则说明有比L更长的公共前缀，这就矛盾了，所以S[k...k+m]这样的字符串是不存在的。

好了，这下kmp的原理我们知道了，接下来说next数组是如何构造的：

其实求next数组相当于模式串P自己跟自己做kmp，然后将最大的匹配结果记录在对应位置，所以实际上求next数组的代码跟kmp是几乎一样的。

模板代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int M=1e6+;

 int nxt[M];
 char s[M],p[M];

 //获得next数组
 void getnext(char *p,int len){
     int i,j;
     i=,j=nxt[]=-;
     while(i<len){
         while(j!=-&&p[i]!=p[j]) j=nxt[j];
         nxt[++i]=++j;
     }
 }
 //返回p在s中第一次出现的位置
 void kmp(char *s,char *p){
     int len1,len2,i,j;
     i=j=;
     len1=strlen(s);
     len2=strlen(p);
     getnext(p,len2);
     while(i<len1){
         while(j!=-&&s[i]!=p[j]) j=nxt[j];
         i++,j++;
         if(j==len2)
             return i-len2+;
     }
     return -;
 }

KMP常见题型：

一、字符串匹配，求出模式串P在S中是否存在，输出第一次出现的位置

HDU 1711

二、求模式串P在S中的出现次数（注意分可重和不可重的情况）

HDU 1686

三、求所有公共前后缀(既是前缀又是后缀)

POJ 2752

四、求字符串循环节

HDU 3746（找最小循环节）

FZU 1901(求所有循环节)

五、求所有S的前缀在S中出现次数之和

HDU 3336

六、最大最小表示

HDU 3374