C基础 - 终结 Size Balanced Tree

引言 - 初识 Size Balanced Tree

　　最近在抽细碎的时间看和学习 random 的 randnet 小型网络库.

　　iamrandom/randnet - https://github.com/iamrandom/randnet (1)

　　了解到 陈启峰 2006-12-29 高中的时候写的论文 Size Balanced Tree(一种变种的 AVI 树) 感觉好精彩.

　　就着手翻译成实战代码.

　　陈启峰 Size Balanced Tree - https://files.cnblogs.com/files/life2refuel/%E9%99%88%E5%90%AF%E5%B3%B0%E3%80%8ASize-Balanced-Tree%E3%80%8B.pdf (2)

　   翻译过程中前驱和后继参照了下面同行的代码

　　 二叉查找树的前驱后继 - http://www.cnblogs.com/Renyi-Fan/p/8252227.html (3)

: )　 - , -

　　推荐朋友学习的时候, 可以先看 (2) 和 (3) . 其中 (3) 最简单, 看完之后应该收获满满.

对于 (2) 还是深深佩服的, 毕竟一样大时候, 才刚脱离趣味玩泥巴. 大佬就可以证明算法的完备性.  如果你看到

(2) 证明部分,  这里不妨补充一些关于 f[h] 求证过程.

其实也就是高中二阶等比数列求证.

　　那后面就开始扯了正题了  : ) 如何用 C 实现上面论文思路, 用于实战开发中.. 我这里抛砖砸高铁.  -:

前言 - 结构接口先行

　　先看设计的数据结构

#ifndef _H_STREE
#define _H_STREE

typedef unsigned long long stree_key_t;

typedef union {
    void * ptr;
    double number;
    signed long long i;
    unsigned long long u;
} stree_value_t;

struct stree {
    struct stree * left;    // 左子树
    struct stree * right;   // 右子树
    unsigned size;          // 树节点个数

    stree_key_t key;        // tree node key
    stree_value_t value;    // tree node value
};

typedef struct stree * stree_t;

inline unsigned stree_size(const struct stree * const node) {
    return node ? node->size : ;
}

#endif//_H_STREE

Size Balanced Tree 中多了一个特色节点 unsigned size; 用户记录当前树上节点个数.  相比 red black tree

后者多记录了 父亲节点和红黑性质. 每种平衡搜索树, 都有自己的特殊字段. 看的出后续核心操作都是

围绕 unsigend size; 字段.

(对于 key 和 value 设计持开放态度. 其中 key 是必须的, 不过这里直接 unsigned long long 走起了)

首先看看最好理解的旋转部分(出道就是巅峰), 的 rotate 旋转操作

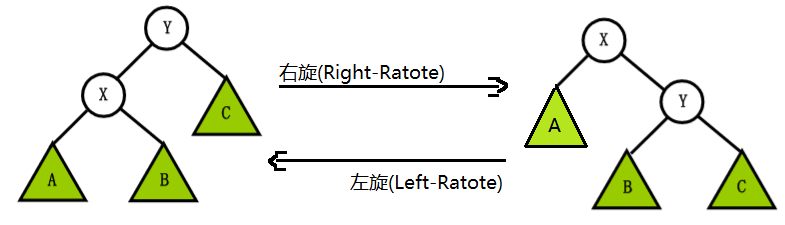
// stree_left_rotate - size tree left rotate
static void stree_left_rotate(stree_t * pode) {
    stree_t node = *pode;
    stree_t right = node->right;

    node->right = right->left;
    right->left = node;
    right->size = node->size;
    node->size = stree_size(node->left) + stree_size(node->right) + ;

    *pode = right;
}

// stree_right_rotate - size tree right rotate
//
//           (y)   left rotate      (x)
//          /   \  ------------>   /   \
//        (x)   [C]              [A]   (y)
//       /   \     <------------      /   \
//      [A]  [B]    right rotate    [B]   [C]
//
static void stree_right_rotate(stree_t * pode) {
    stree_t node = *pode;
    stree_t left = node->left;

    node->left = left->right;
    left->right = node;
    left->size = node->size;
    node->size = stree_size(node->left) + stree_size(node->right) + ;

    *pode = left;
}

强烈好好看看练习练习, 否则后面更加不懂.

　　: ) 好想说, 后面不用看了, 复制我的代码. 如果用的时候用吧, 否则就别再见了.

正文 - 有时候要认命

当前核心是翻译论文, 并且终结 Size Balanced Tree 各种花式的代码.

细节部分看论文, 看作者原文思路.这里只是贴代码, 带你感受一下一个上的了台面的 Size Balanced Tree 实现  ~

stree.h

#ifndef _H_STREE
#define _H_STREE

typedef unsigned long long stree_key_t;

typedef union {
    void * ptr;
    double number;
    signed long long i;
    unsigned long long u;
} stree_value_t;

struct stree {
    struct stree * left;    // 左子树
    struct stree * right;   // 右子树
    unsigned size;          // 树节点个数

    stree_key_t key;        // tree node key
    stree_value_t value;    // tree node value
};

typedef struct stree * stree_t;

inline unsigned stree_size(const struct stree * const node) {
    return node ? node->size : ;
}

//
// stree_delete - Size Balanced Tree delete destroy
// poot     : 指向 tree 对象指针
// return   : void
//
extern void stree_delete(stree_t * poot);

//
// stree_insert - size tree insert node
// poot     : 指向 tree 对象指针
// key      : 插入 node key
// value    : 插入 node value
// return   : void
//
extern void stree_insert(stree_t * poot, stree_key_t key, stree_value_t value);

//
// stree_remove - size tree remove node
// poot     : 指向 tree 对象指针
// key      : 查找 node key
// return   : void
//
extern void stree_remove(stree_t * poot, stree_key_t key);

//
// stree_find - 寻找到指定的节点
// root     : tree 对象
// key      : 查找 node key
// return   : 查找 tree node, NULL 表示没有
//
extern stree_t stree_find(stree_t root, stree_key_t key);

//
// stree_rank - 返回 key 在 root 树中排名, 也就是比 key 小的那颗树的大小上加 1
// root     : tree 对象
// key      : 查找 node key
// return   : 排名
//
extern unsigned stree_rank(stree_t root, stree_key_t key);

//
// stree_select - root 根节点树种排名为 k 的节点
// root     : tree 对象
// k        : 排名 [1, stree_size(root)]
// return   : 返回查询到节点
//
extern stree_t stree_select(stree_t root, unsigned k);

//
// stree_pred - 查找 root 前驱节点, 比 key 小的最大的数
// root     : tree 对象
// key      : 查找 node key
// return   : 返回查询到节点
//
extern stree_t stree_pred(stree_t root, stree_key_t key);

//
// stree_succ - 查找 root 后继节点, 比 key 大的最小的数
// root     : tree 对象
// key      : 查找 node key
// return   : 返回查询到节点
//
extern stree_t stree_succ(stree_t root, stree_key_t key);

#endif//_H_STREE

　　上面 delete 和 remove 单词和论文中比对有些不一样. 因为在 C / C++ 中 delete 语义是销毁.

所以采用 remove 去除的节点的语义单词. 应该更加贴合实际开发的代码函数定义.

stree.c

#include "stree.h"
#include <stdlib.h>
#include <stdbool.h>

static void stree_free(stree_t root) {
    if (root->left)
        stree_free(root->left);
    if (root->right)
        stree_free(root->right);
    free(root);
}

//
// stree_delete - Size Balanced Tree delete destroy
// poot     : 指向 tree 对象指针
// return   : void
//
inline void
stree_delete(stree_t * poot) {
    if (!poot || !*poot)
        return;
    stree_free(*poot);
    *poot = NULL;
}

// stree_left_rotate - size tree left rotate
static void stree_left_rotate(stree_t * pode) {
    stree_t node = *pode;
    stree_t right = node->right;

    node->right = right->left;
    right->left = node;
    right->size = node->size;
    node->size = stree_size(node->left) + stree_size(node->right) + ;

    *pode = right;
}

// stree_right_rotate - size tree right rotate
//
//           (y)   left rotate      (x)
//          /   \  ------------>   /   \
//        (x)   [C]              [A]   (y)
//       /   \     <------------      /   \
//      [A]  [B]    right rotate    [B]   [C]
//
static void stree_right_rotate(stree_t * pode) {
    stree_t node = *pode;
    stree_t left = node->left;

    node->left = left->right;
    left->right = node;
    left->size = node->size;
    node->size = stree_size(node->left) + stree_size(node->right) + ;

    *pode = left;
}

// stree_maintain - Size Balanced Tree Maintain
static void stree_maintain(stree_t * pode, bool flag) {
    unsigned size;
    stree_t node = *pode;
    if (!node) return;

    if (!flag) {
        if (!node->left) return;

        size = stree_size(node->right);
        if (size < stree_size(node->left->left))
            stree_right_rotate(pode);
        else if (size < stree_size(node->left->right)) {
            stree_left_rotate(&node->left);
            stree_right_rotate(pode);
        } else return;

        stree_maintain(&node->left, false);
    } else {
        if (!node->right) return;

        size = stree_size(node->left);
        if (size < stree_size(node->right->right))
            stree_left_rotate(pode);
        else if (size < stree_size(node->right->left)) {
            stree_right_rotate(&node->right);
            stree_left_rotate(pode);
        } else return;

        stree_maintain(&node->right, true);
    }

    stree_maintain(pode, false);
    stree_maintain(pode, true);
}

static void stree_insert_node(stree_t * poot, stree_t node) {
    bool flag;
    stree_t root = *poot;
    if (!root) {
        (*poot = node)->size = ;
        return;
    }

    ++root->size; // 插入到非空树, 节点数加 1
    if ((flag = node->key < root->key))
        stree_insert_node(&root->left, node);
    else
        stree_insert_node(&root->right, node);
    stree_maintain(poot, !flag);
}

//
// stree_insert - size tree insert node
// poot     : 指向 tree 对象指针
// key      : 插入 node key
// value    : 插入 node value
// return   : void
//
inline void
stree_insert(stree_t * poot, stree_key_t key, stree_value_t value) {
    stree_t node = calloc(, sizeof(struct stree));
    node->key = key;
    node->value = value;
    stree_insert_node(poot, node);
}

static stree_t stree_remove_node(stree_t * pode, const stree_key_t key, bool find) {
    stree_t record;
    stree_t node = *pode;
    if (!node) return NULL;

    if (find && !node->right) {
        //  the right end node of right child tree replace the delete node
        *pode = node->left;
        return node;
    }

    if (!find && key == node->key) {
        if (node->size == ) {
            // leaf node, need delete
            *pode = NULL;
            return node;
        }
        if (node->size == ) {
            // single branch node, need child node replace delete node
            record = node->left ? node->left : node->right;
            node->left = node->right = NULL;
        } else {
            // max key node of left tree replace pnode
            record = stree_remove_node(&node->left, key, true);
        }
        if (record) {
            node->key = record->key;
            node->value = record->value;
        }
        --node->size;
        stree_maintain(pode, true);
    } else if (!find && key < node->key) {
        record = stree_remove_node(&node->left, key, false);
        if (record)
            --node->size;
    } else {
        record = stree_remove_node(&node->right, key, find);
        if (record)
            --node->size;
    }

    stree_maintain(pode, !find && key < node->key);
    return record;
}

//
// stree_remove - size tree remove node
// poot     : 指向 tree 对象指针
// key      : 查找 node key
// return   : void
//
inline void
stree_remove(stree_t * poot, stree_key_t key) {
    stree_t node;
    if (!poot) return;
    node = stree_remove_node(poot, key, false);
    if (node) free(node);
}

//
// stree_find - 寻找到指定的节点
// root     : tree 对象
// key      : 查找 node key
// return   : 查找 tree node, NULL 表示没有
//
stree_t
stree_find(stree_t root, stree_key_t key) {
    while (root) {
        if (key < root->key)
            root = root->left;
        else if (root->key < key)
            root = root->right;
        else break;
    }
    return root;
}

//
// stree_rank - 返回 key 在 root 树中排名, 也就是比 key 小的那颗树的大小上加 1
// root     : tree 对象
// key      : 查找 node key
// return   : 排名
//
unsigned
stree_rank(stree_t root, stree_key_t key) {
    int k = ;
    while (root) {
        if (key < root->key)
            root = root->left;
        else if (root->key < key) {
            k += stree_size(root->left) + ;
            root = root->right;
        } else {
            k += stree_size(root->left);
            break;
        }
    }
    return k;
}

//
// stree_select - root 根节点树种排名为 k 的节点
// root     : tree 对象
// k        : 排名 [1, stree_size(root)]
// return   : 返回查询到节点
//
stree_t
stree_select(stree_t root, unsigned k) {
    while (root) {
        unsigned size = stree_size(root->left);
        if (k < size)
            root = root->left;
        else if (size < k) {
            root = root->right;
            k -= size + ;
        } else break;
    }
    return root;
}

/*
 前驱节点
    1. 若一个节点有左子树，那么该节点的前驱节点是其左子树中 key 值最大的节点
    2. 若一个节点没有左子树，那么判断该节点和其父节点的关系
        2.1 若该节点是其父节点的右孩子，那么该节点的前驱节点即为其父节点。
        2.2 若该节点是其父节点的左孩子，那么需要沿着其父亲节点一直向树的顶端寻找，
            直到找到一个节点P，P节点是其父节点Q的右孩子，那么Q就是该节点的后继节点

 */

static stree_t stree_get_right(stree_t root) {
    if (root) {
        while (root->right)
            root = root->right;
    }
    return root;
}

static stree_t stree_get_right_p(stree_t root, stree_key_t key, stree_t * pq, stree_t * pr) {
    while (root) {
        if (key == root->key)
            return root;

        *pq = root;
        if (key < root->key)
            root = root->left;
        else {
            *pr = root; // 出现右拐点, 父节点 Q 的右孩子
            root = root->right;
        }
    }
    return root;
}

//
// stree_pred - 查找 root 前驱节点, 比 key 小的最大的数
// root     : tree 对象
// key      : 查找 node key
// return   : 返回查询到节点
//
stree_t
stree_pred(stree_t root, stree_key_t key) {
    if (root) {
        stree_t q = NULL, r = NULL;
        stree_t p = stree_get_right_p(root, key, &q, &r);
        if (!p)
            return NULL;
        // 有左子树
        if (p->left)
            return stree_get_right(p->right);

        // 没有前驱节点的情况
        if ((!p) || (p && !r))
            return NULL;

        // 没有左子树, 其父节点的右节点
        if (p == q->right)
            return q;
        // 没有左子树, 是其父节点的左节点
        return r;
    }
    return root;
}

/*
 后继节点
    1. 若一个节点有右子树，那么该节点的后继节点是其右子树中 key 值最小的节点
    2. 若一个节点没有右子树，那么判断该节点和其父节点的关系
        2.1 若该节点是其父节点的左孩子，那么该节点的后继结点即为其父节点
        2.2 若该节点是其父节点的右孩子，那么需要沿着其父亲节点一直向树的顶端寻找，
            直到找到一个节点P，P节点是其父节点Q的左孩子，那么Q就是该节点的后继节点
 */

static stree_t stree_get_left(stree_t root) {
    if (root) {
        while (root->left)
            root = root->left;
    }
    return root;
}

static stree_t stree_get_left_p(stree_t root, stree_key_t key, stree_t * pq, stree_t * pr) {
    while (root) {
        if (root->key == key)
            return root;

        *pq = root; // 设置父亲节点
        if (root->key < key)
            root = root->right;
        else {
            *pr = root; // 出现左拐点, 父节点 Q 的左孩子
            root = root->left;
        }
    }
    return root;
}

//
// stree_succ - 查找 root 后继节点, 比 key 大的最小的数
// root     : tree 对象
// key      : 查找 node key
// return   : 返回查询到节点
//
stree_t
stree_succ(stree_t root, stree_key_t key) {
    if (root) {
        stree_t q = NULL, r = NULL;
        stree_t p = stree_get_left_p(root, key, &q, &r);
        if (!p)
            return NULL;
        // 有右子树
        if (p->right)
            return stree_get_right(p->right);

        // 没有前驱节点的情况
        if ((!p) || (p && !r))
            return NULL;

        // 没有右子树, 其父节点的左节点
        if (p == q->left)
            return q;
        // 没有右子树, 是其父节点的右节点
        return r;
    }
    return root;
}

　　这里也简单写个测试例子, 保证核心逻辑插入和查找还有销毁可以用.

main.c

#include <stdio.h>
#include <stdlib.h>

#include "stree.h"

//
// Size Balanced Tree
//
int main(int argc, char * argv[]) {
    stree_t root = NULL;

    // 插入数据
    for (int i = ; i < ; i++)
        stree_insert(&root, i, (stree_value_t) { .i = i });

    int key = ;
    stree_t node = stree_find(root, key);
    if (NULL == node) {
        fprintf(stderr, "stree_find is error key = %d\n", key);
        exit(EXIT_FAILURE);
    }
    printf("key = %d, node = %lld\n", key, node->value.i);

    stree_remove(&root, key);
    node = stree_find(root, key);
    if (node) {
        fprintf(stderr, "stree_find is error key = %d\n", key);
        exit(EXIT_FAILURE);
    }
    printf("stree_remove is success key = %d\n", key);

    stree_delete(&root);
    return ;
}

论文 + C 代码互相配合, 希望能对准备尝试的人有些作用.  长舒一口气.

抛开图, 面试最难不过二叉树 ~,~

开发中 tree set hash list vector 非常常见, 其中 tree 常被 hash 和 set 抢掉运用场景.  例如 id 管理.

但二叉树是批量搜索业务的基石 (别说跳表). 不管如何你都得尝试跃迁过 ~-~

后记 - 开心就好

　　错误是难免的, 欢迎交流指正, 互相提升 ~

　　負け犬達のレクイエム - http://music.163.com/m/song?id=29751658&userid=16529894

: )

故事的开头，总是惊鸿一瞥，一眼千年，故事的结尾，总是潇洒转身，渐行渐远

-: