Statistical Concepts and Market Returns

Categories of statistics

Descriptive statistics: used to summarize the important characteristics of large data sets.
Inferential statistics: pertain to the procedures used to make forecasts, estimates, or judgments about a large set of data on the basis of the statistical characteristics of a sample.

Measures of Central Tendency

When describing investments, measures of central tendency provide an indication of an investment's expected return.

Arithmetic mean (算术平均)
Geometric mean (几何平均): often used when calculating investment returns over multiple periods or when measuring compound growth rates.
Weighted mean (加权平均)
Median (中位数): the midpoint of a data set when the data is arranged in ascending or decending order.
Mode (众数): the value that occurs most frequently in a data set. A data set may have more than one mode or even no mode.
Harmonic mean(调和平均数/倒数平均数): used for certain computations, wuch as the average cost of shares purchased over time. 是总体各统计变量倒数的算术平均数的倒数

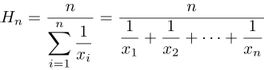
Note: The geometric mean is always less than or equal to the arithmetic mean, and the difference increases as the dispersion of the observations increases. The only time the arithmetic and geometric means are equal is when there is no variability in the observations (i.e. all observations are equal)

Note: For values that are not all equal: harmonic mean < geometric mean < arithmetic mean. This mathematical fact is the basis for the claimed benefit of purchasing the same dollar amount of mutual fund shares each month or each week. Some refer to this practice as "dollar cost averaging"

Note: modal interval: for any frequency distribution, the interval with the greatest frequency is referred to as the modal interval. 模式区间：发生频率最高的区间。

均值(mean)和平均值(average)在很多情况下可以不加区分地使用，但是两者还是有所区别：1)样本的“均值”是根据上面的算术平均公式计算得出2)"平均值"是若干种可以描述样本的典型值或集中趋势(central tendency)的汇总统计量之一。

Measures of Dispersion

When describing investment, measures of dispersion indicate the riskiness of an investment.

Dispersion is defined as the variability around the central tendency. The common theme in finance and investmentss is the tradeoff between reward and variability, where the central tendency is the measure of the reward and dispersion is a measure of risk.

Range (范围): range = maximum value - minimum value
Mean absolute deviation (MAD/平均绝对偏差): the average of the absolute values of the deviations of individual observations from the arithmetic mean.
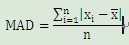
Variance (方差)：
Standard Deviation(标准差)：

Note: The most noteworthy difference from the formula for population variance is that the denominator for s^2 is n-1, one less than the sampe size n, where σ^2 uses the entire population size N. Based on the mathematical theory behind statistical procedures, the use of the entire number of sample observations, n instead of n-1 as the divisor in the commputation of s^2, will systematically underestimate the population parameter σ^2, particular for small sample sizes. This sysmatic underestimation causes the same variance to be what is referrerd to as biased estimator of the population variance. Using n-1 instead of n iin the denominator, however, improves the statistical properties of s^2 as an estimator of σ^2. Thus, s^2 is considdered to be an unbiased estimator of σ^2.

Chebyshev's Inequality

Chebyshev's inequality(切比雪夫不等式) states that for any set of observations, whether sample or population data and regardless of the shape of the distribution, the percentage of the observations that lie within k standard deviations of the mean is at least 1-1/k^2 for k > 1.

The importance of Chebyshev's inequality is that is applies to any distribution.

Coefficient of Variation (变异系数/离散系数)

Relative disperation is the amount of variability in a distribution relative to a reference point or benchmark. Relative disperation is commonly measured with the coefficient of vairation(CV).

离散系数，离散系数又称变异系数，是统计学当中的常用统计指标，主要用于比较不同水平的变量数列的离散程度及平均数的代表性。

CV = (standard devition of x)/(average value of x)

CV measures the amount of dispersion in a distribution relative to the distribution's mean. In an investments setting, the CV is used to measure the risk(variability) per unit of expected return(mean).

Sharpe Ratio

The Sharpe measure(a.k.a., the Sharpe ratio or reward-to-variability ratio) is widely used for investment performance measurement and measures excess return per unit of risk.

夏普比率：反应风险及回报的比率。测量组合回报的风险，将高于无风险回报的部分除以某一时段内的标准差，得出的结果就是每一单位风险产生的超额回报。比率越高，调整风险后的回报越高。

Skewness(偏度)

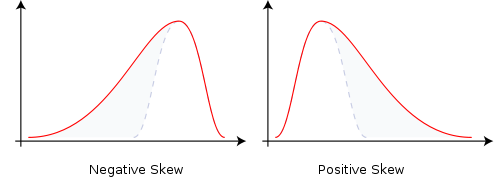
Skewness, or skew, refers to the extent to which a distribution is not sysmmetrical. Nonsysmmetrical distributions may be either positively or negatively skewe and result from the occurrence of outliers in the data set. Outliers are observations with extraordinarily large values, either positve or negative.

A positively skewed distribution is characterized by many outliers in the upper region or right tail. A positively skewed distribution is said to be skewed right because of its relatively long upper(right) tail.
A negatively skewed distribution has a disproportionately large amount of outliers that fall within its lower(left) tail. A negatively skewed distribution is said to be skewed left because of its lower tail.

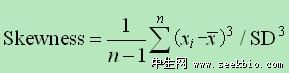
Values of Sk in excess of 0.5 in absolute value indicate significant levels of skewness.

Kurtosis(峰度)

Kurtosis is a measure of the degree to which a distribution is more or less "peaked" than a normal distribution. Leptokurtic(频率分配曲线的尖顶峰度) describes a distribution that is more peaked tha a normal distribution, whereas platykurtic (低峰态分布) refers to a distribution that is less peeked, or flatter than a normal distribution. A distribution is mesokurtic(常态峰) if it has the same kurtosis as a normal distribution.

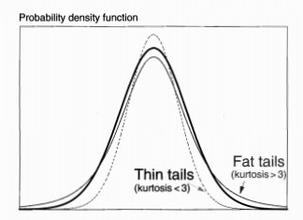
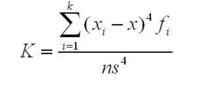
A distribution is said to exhibit excess kurtosis if it has either more or less kurtosis than the normal distribution. The computed kurtosis for all normal distribution is 3. A normal distribution has excess kurtosis equal to 0, a leptokurtic distribution has excess kurtosis greater than 0, and platykurtic distributions will have excess kurtosis less than 0.

In general, greater positive kurtosis and more negative skew in returns distributions indicates increased risk.

Excess kurtosis values that exceed 1.0 in absolute value are considered large.

excess kurtosis=sample kurtosis-3