Lattice Point or Not UVA - 11768（拓展欧几里得）

原文地址：https://www.cnblogs.com/zyb993963526/p/6783532.html

题意：

给定两个点A（x1，y1）和B（x2，y2），均为0.1的整数倍。统计选段AB穿过多少个整点。

思路：

做了这道题之后对于扩展欧几里得有了全面的了解。

根据两点式公式求出直线 ，那么ax+by=c 中的a、b、c都可以确定下来了。

接下来首先去计算出一组解(x0,y0)，因为根据这一组解，你可以写出它的任意解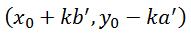，其中，K取任何整数。

需要注意的是，这个 a' 和 b' 是很重要的，比如说 b' ，它代表的是x每隔 b' ，就会出现一个整点。

所以这道题目的关键就是，我们先求出一组解，然后通过它的 b' 将x0改变成x，使得x在[x1,x2]区间之内，这样每 b' 个单位就有一个整点了，即

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<queue>
#include<cmath>
#include<map>
using namespace std;

typedef long long LL;
double X1,Y1,X2,Y2;

void gcd(LL a,LL b,LL& d,LL& x,LL& y)
{
    if(!b)  {d=a;x=;y=;}
    else { gcd(b,a%b,d,y,x); y-=x*(a/b);}
}

LL solve()
{
    LL x1=X1*, y1=Y1*, x2=X2*, y2=Y2*;
    if(x1==x2)                    //平行y轴
    {
        if(x1%)  return ;      //原来的X1为小数,肯定不是整点
        if(Y2<Y1)  swap(Y1,Y2);
        return floor(Y2)-ceil(Y1)+;
    }
    if(y1==y2)
    {
        if(y1%)  return ;
        if(X2<X1)  swap(X1,X2);
        return  floor(X2)-ceil(X1)+;
    }
    LL a=(y2-y1)*, b=(x1-x2)*, c=y2*x1-y1*x2;  //c相当于扩大了100倍，所以前面还得乘10
    LL d,x,y;
    gcd(a,b,d,x,y);
    if(c%d)   return ;      //扩展欧几里得算法无解的判断

    x=x*c/d; y=y*c/d;        //获得一组整数解(x,y)
    b=abs(b/d);             //这里的b其实就是b'

    if(X1>X2)   swap(X1,X2);
    x1=ceil(X1);
    x2=floor(X2);
    if(x1>x2) return ;

    x=x+(x1-x)/b*b;        //使x进入[x1,x2]的区间内
    if(x<x1)  x+=b;
    if(x>x2)  return ;
    return (x2-x)/b+;
}

int main()
{
    //freopen("D:\\input.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lf%lf%lf%lf",&X1,&Y1,&X2,&Y2);
        LL ans = solve();
        printf("%lld\n",ans);
    }
    return ;
}

思路：

做了这道题之后对于扩展欧几里得有了全面的了解。

根据两点式公式求出直线 ，那么ax+by=c 中的a、b、c都可以确定下来了。

接下来首先去计算出一组解(x0,y0)，因为根据这一组解，你可以写出它的任意解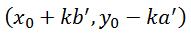，其中，K取任何整数。

需要注意的是，这个 a' 和 b' 是很重要的，比如说 b' ，它代表的是x每隔 b' ，就会出现一个整点。

所以这道题目的关键就是，我们先求出一组解，然后通过它的 b' 将x0改变成x，使得x在[x1,x2]区间之内，这样每 b' 个单位就有一个整点了，即