poj3735—Training little cats（特殊操作转化为矩阵操作）

题目链接：http://poj.org/problem?id=3735

题目意思：

调教猫咪：有n只饥渴的猫咪，现有一组羞耻连续操作，由k个操作组成，全部选自：

1. g i 给第i只猫咪一颗花生

2. e i 让第i只猫咪吃光它的花生

3. s i j 交换猫咪i与猫咪j的花生

现将上述一组连续操作做m次后，求每只猫咪有多少颗花生？

思路：这道题难点在如何把这种奇怪的操作转化为矩阵操作，网络上看到一个画的很好的图，这里直接偷过来。

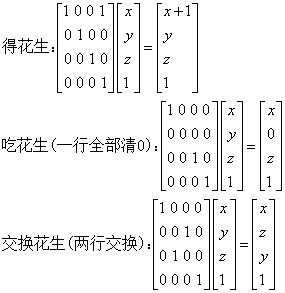
现在，对于每一个操作我们都可以得到一个转置矩阵，把k个操作的矩阵相乘我们可以得到一个新的转置矩阵T。A * T 表示我们经过一组操作，类似我们可以得到经过m组操作的矩阵为 A * T ^ m,最终矩阵的[0][1~n]即为答案。

上述的做法比较直观，但是实现过于麻烦，因为要构造k个不同矩阵。有没有别的方法可以直接构造转置矩阵T？答案是肯定的。

我们还是以单位矩阵为基础：

对于第一种操作g i，我们使Mat[0][i] = Mat[0][i] + 1
对于第二种操作e i，我们使矩阵的第i列清零；
对于第三种操作s i j，我们使第i列与第j列互换。
这样实现的话，我们始终在处理一个矩阵，免去构造k个矩阵的麻烦。
至此，构造转置矩阵T就完成了，接下来只需用矩阵快速幂求出 A * T ^ m即可，还有一个注意的地方，该题需要用到long long。

这里还要说一下T*A=A*T的转置。

代码：

 //Author: xiaowuga
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #define maxx INT_MAX
 #define minn INT_MIN
 #define inf 0x3f3f3f3f
 #define N  105
 using namespace std;
 typedef long long ll;
 ll  n,size;//第n项，矩阵大小
 struct Matrix{
     ll mat[N][N];
     void clear(){
         memset(mat,,sizeof(mat));
     }
     Matrix operator * (const Matrix & m) const{
         Matrix tmp;
         int i ,j,k;
         tmp.clear();
         for( i=;i<size;i++)
             for( k=;k<size;k++){
                 if(mat[i][k]==) continue;
                 for( j=;j<size;j++){
                     tmp.mat[i][j]+=mat[i][k]*m.mat[k][j];
                 }
             }
         return tmp;
     }
 };
 void POW(Matrix m,ll k){
     Matrix ans;
     memset(ans.mat,,sizeof(ans.mat));
     for(int i=;i<size;i++) ans.mat[i][i]=;
     while(k){
         if(k&) ans=ans*m;
         k/=;
         m=m*m;
     }
     for(int i=;i<size;i++){
         cout<<ans.mat[][i]<<" ";
     }
     cout<<endl;
 }
 int main() {
     Matrix m;
     int k;
     while(cin>>size>>n>>k&&(size+n+k)){
         size++;
         m.clear();
         for(int i=;i<size;i++) m.mat[i][i]=;
         for(int i=;i<k;i++){
             char t[];
             int num1,num2;
             cin>>t;
             if(t[]=='g'){
                 cin>>num1;
                 m.mat[][num1]++;
             }
             else if(t[]=='e'){
                 cin>>num1;
                 for(int j=;j<size;j++){
                     m.mat[j][num1]=;
                 }
             }
             else{
                 cin>>num1>>num2;
                 for(int j=;j<size;j++)
                     swap(m.mat[j][num1],m.mat[j][num2]);
             }
         }
         POW(m,n);
     }
     return ;
 }