线段树(Segment Tree)（转）

原文链接：线段树(Segment Tree)

1、概述

线段树，也叫区间树，是一个完全二叉树，它在各个节点保存一条线段（即“子数组”），因而常用于解决数列维护问题，基本能保证每个操作的复杂度为O(lgN)。

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

本文地址：http://www.cnblogs.com/archimedes/p/segment-tree.html，转载请注明源地址。

2、线段树基本操作

线段树的基本操作主要包括构造线段树，区间查询和区间修改。

（1）线段树构造

首先介绍构造线段树的方法：让根节点表示区间[0,N-1]，即所有N个数所组成的一个区间，然后，把区间分成两半，分别由左右子树表示。不难证明，这样的线段树的节点数只有2N-1个，是O(N)级别的，如图：

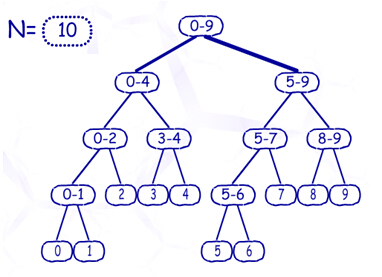
节点定义如下：

typedef struct node {
    int l;        //线段的左端点
    int r;        //线段的左端点
    int value;    //线段上的值
}node;

线段树的构建

bulid//以节点v为根建树、v对应区间为[l,r]
{
    对节点v初始化
     if (l!=r) {
          以v的左孩子为根建树，区间为[l,(l+r)/2]
          以v的右孩子为根建树，区间为[(l+r)/2+1,r]
    }
}

完整的建树代码如下:

#define N 10000
node tree[N];
void bulid(int l, int r, int v) //对结点v进行建立，区间为l~r
{
    tree[v].l = l;
    tree[v].r = r;
    if(l == r) {
        //进行结点的初始化
        tree[v].value = a[r];
        return;
    }
    int mid = (l + r) / 2;
    bulid(v * 2, l, mid);
    bulid(v * 2 + 1, mid + 1, r);
    //根据左右儿子更新当前结点
    tree[v].value = tree[v * 2].value + tree[v * 2 + 1].value;
}

更新

当在a[i]~a[j]上的所有的元素都加上一个值c的时候

如果a[i]~a[j]刚还是一个完整段的时候，直接将这个段的value值加上c*(r-l+1)

当更新的区间不是一个完整段的时候，采用一种记录增量的方法：给每个节点增加一个域：int add，记录更新操作的增量c，初始的时候add均为0，比如当对2~5区间更新后，给该结点的add加上一个值c，再下次要对2~3结点进行更新或查询时，再将add传递到下面的孩子结点中去

完整的更新树代码如下:

typedef struct node {
    int l;        //线段的左端点
    int r;        //线段的左端点
    int value;    //线段上的值
    int add;
}node;
void update(int v, int r, int l, int m)//更新区间l~r加上数m
{
    if(tree[v].l == l && tree[v].r == r) {  //找到，更新并记录增量
        tree[v].value += m * (r - l + 1);
        tree[v].add = m;
        return;
    }
    if(tree[v].add) {
        tree[2 * v].add += tree[v].add;
        tree[2 * v + 1].add += tree[v].add;
        tree[v].add = 0;
    }
    int mid = (tree[v].l + tree[v].r) / 2;
    if(r <= mid) {
        update(v * 2, l, r, m);   //只对左儿子更新
    } else {
        if(l > mid) {
            update(v * 2 + 1, l, r, m);  //只对右儿子更新
        } else {                        //区间横跨左右儿子区间，对其两者均进行更新
            update(v * 2, l, mid, m);
            update(v * 2 + 1, mid + 1, r, m);
        }
    }
}

查询

查询区间l~r上的value值

void query(int v, int l, int r)  //当前查询结点为v，要查询的区间为l~r
{
    if(tree[v].l == l && tree[v].r == r) {
        ans += tree[v].value;
        return;
    }
    if(tree[v].add) {
        tree[v * 2].add += tree[v].add;
        tree[v * 2 + 1].add += tree[v].add;
        tree[v].add = 0;
    }
    int mid = (tree[v].l + tree[v].r) / 2;
    if(r <= mid) {
        query(v * 2, l, r);   //要查询的区间都在左儿子
    } else {
        if(l > mid) {
            query(v * 2 + 1, l, r);  //要查询的区间都在左儿子
        } else {                //要查询的区间横跨左右孩子
            query(v * 2, l, mid);
            query(v * 2 + 1, mid + 1, r);
        }
    }
}

编程实践

poj2182 Lost Cows

Description

N (2 <= N <= 8,000) cows have unique brands in the range 1..N. In a spectacular display of poor judgment, they visited the neighborhood 'watering hole' and drank a few too many beers before dinner. When it was time to line up for their evening meal, they did not line up in the required ascending numerical order of their brands. 

Regrettably, FJ does not have a way to sort them. Furthermore, he's not very good at observing problems. Instead of writing down each cow's brand, he determined a rather silly statistic: For each cow in line, he knows the number of cows that precede that cow in line that do, in fact, have smaller brands than that cow. 

Given this data, tell FJ the exact ordering of the cows.
Input

* Line 1: A single integer, N 

* Lines 2..N: These N-1 lines describe the number of cows that precede a given cow in line and have brands smaller than that cow. Of course, no cows precede the first cow in line, so she is not listed. Line 2 of the input describes the number of preceding cows whose brands are smaller than the cow in slot #2; line 3 describes the number of preceding cows whose brands are smaller than the cow in slot #3; and so on.
Output

* Lines 1..N: Each of the N lines of output tells the brand of a cow in line. Line #1 of the output tells the brand of the first cow in line; line 2 tells the brand of the second cow; and so on.
Sample Input

5
1
2
1
0
Sample Output

2
4
5
3
1

#include<stdio.h>
#include<stdlib.h>
#define N 10000
int small[N], ans[N];
struct segment {
    int lc, rc, len;
};
struct segment s[ * N];
void bulid(int root, int lc, int rc)  /*建树*/
{
    s[root].lc = lc;
    s[root].rc = rc;
    s[root].len = rc - lc + ;
    if(rc == lc) return;
    bulid( * root, lc, (lc + rc) / );
    bulid( * root + , (lc + rc) /  + , rc);
}
int query(int root, int k)
{
    s[root].len--;
    if(s[root].lc == s[root].rc) return s[root].lc;
    else if(k <= s[ * root].len) {
        return query( * root, k);
    } else {
        return query( * root + , k - s[ * root].len);
    }
}

int main()
{
    int n, i;
    scanf("%d", &n);
    for(i = ; i <=n; i++)
        scanf("%d", &small[i]);
    small[] = ;
    bulid(, , n);
    for(i = n; i >= ; i--)
        ans[i] = query(, small[i] + );
    for(i = ; i <= n; i++)
        printf("%d\n", ans[i]);
    return ;
}

leetcode编程题307 Range Sum Query - Mutable

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

The update(i, val) function modifies nums by updating the element at index i to val.

Example:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:

The array is only modifiable by the update function.
You may assume the number of calls to update and sumRange function is distributed evenly.

public class NumArray {

        private class SegmentTreeNode{
            int start;
            int end;
            int sum;
            SegmentTreeNode left;
            SegmentTreeNode right;
            public SegmentTreeNode(int start, int end){
                this.start = start;
                this.end = end;
                this.sum = 0;
                this.left = null;
                this.right = null;
            }
        }

        private SegmentTreeNode buildTree(int[] nums, int s, int e){
            if(s>e)
                return null;
            SegmentTreeNode stn = new SegmentTreeNode(s,e);
            if(s==e){
                stn.sum = nums[s];
            }else{
                int mid = s+(e-s)/2;
                stn.left = buildTree(nums, s, mid);
                stn.right = buildTree(nums, mid+1, e);
                stn.sum = stn.left.sum+stn.right.sum;
            }
            return stn;
        }

        private void update(SegmentTreeNode root, int i, int val){
            if(root.start==root.end){
                root.sum = val;
            }else{
                int mid = root.start + (root.end-root.start)/2;
                if(i<=mid)
                    update(root.left, i, val);
                else if(i>mid)
                    update(root.right, i, val);
                root.sum = root.left.sum + root.right.sum;
            }
        }

        private int sumRange(SegmentTreeNode root, int s, int e){
            if(root.start==s&&root.end==e){
                return root.sum;
            }else{
                int mid = root.start + (root.end-root.start)/2;
                if(e<=mid)
                    return sumRange(root.left, s, e);
                else if(s>mid)
                    return sumRange(root.right, s, e);
                else
                    return sumRange(root.left, s, mid)+sumRange(root.right, mid+1, e);
            }
        }

        SegmentTreeNode root;
        public NumArray(int[] nums) {
            root = buildTree(nums, 0, nums.length-1);
        }

        void update(int i, int val) {
            update(root, i, val);
        }

        public int sumRange(int i, int j) {
            return sumRange(root, i, j);
        }
}

// Your NumArray object will be instantiated and called as such:
// NumArray numArray = new NumArray(nums);
// numArray.sumRange(0, 1);
// numArray.update(1, 10);
// numArray.sumRange(1, 2);

参考链接：

线段树(segment tree)