3D数学基础 KeyNote 1

【计算几何复习要点】

　1、向量加法的几何含意：

　　a+b的释意为：a的尾连上b的头，新建一条从a的尾指向b的头的向量。

　2、向量减法的几何含意：

　　a-b的释意为：尾部相连，新建一个从b的头指向a的头的向量。

　3、点积，内积：

　　对于向量a(Xa，Ya)、向量b(Xb,Yb)，a与b的点积为：Xa*Xb+Ya*Yb。

　　另外 a*b=|a|*|b|*cos(a与b夹角)。通过此公式可通过坐标来计算2向量夹角。

　4、叉积。注意，axb 的结果是一个向量。

　　|aXb| = |a|*|b|*sin(a与b夹角)。几何函数为a向量与b向量组成的面积。

　5、行数和列数相同的矩阵称为方阵。所有非对角线元素都为0的矩阵为对角矩阵。

　6、转置矩阵意味着把矩阵给转换。

参考自《3D数学基础：图像与游戏开发》

【3D数学基础】

1、研究自然数、整数的领域称为离散数学。研究实数的领域称作连续数学。

2、计算机图形学第一准则：近似原则 。如果它看上去是对的，它就是对的。

3、常见坐标系。

　　1）世界坐标系。

　　2）物体坐标系。

　　3）摄像机坐标系。

　　4）惯性坐标系。

4、向量的大小。

　　

5、点积：对应分量的和。

　　

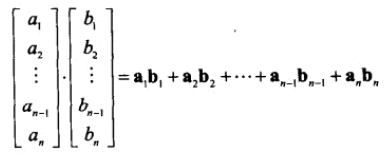
　　点积可以计算向量的夹角：

　　

6、假设有向量v,n，则v可以拆分平行为n的向量 v1、以及垂直于n的向量v2。

　　

　　v1 = |v1|*n / |n| = |v| cos0 *n / |n| = |v||n|cos0*n / |n|^2 = dot(v,n)*n/|n|^2

　　

　　上术计算 v1 的公式，可以略去 cos0 的计算。

　　有了v1，v2就很好求了。 v2 = v - v1

　　

7、叉乘公式。

　　

　　叉乘不满足交换律，即： axb != bxa。但满足反交换律：

　　　　

　　也不满足结合律：

　　　　

　　叉乘满足分配律：
　　　　

　　

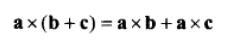
8、矩阵是 row x column，如下面是一个 4x3 的矩阵。

　　

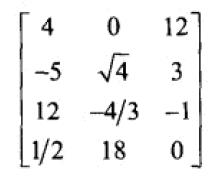
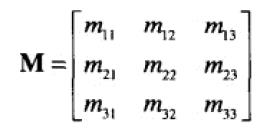
9、两个矩阵积的转置 等于 转置的逆序积。
　　

10、行向量左乘矩阵，结果是行向量；行向量右乘矩阵，结果是无定义。

　　列向量左乘矩阵，结果是无定义；列向量右乘矩阵，结果是列矩阵。

　　并且注意，行向量、列向量的值完全不同。

　　

11、若把矩阵的行解释为基向量，那么乘以该矩阵就相当于执行了一次坐标转换。若有 aM = b，我们就可以说，M可以将a转换到b。

　　

　　

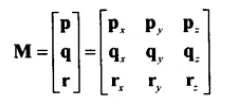
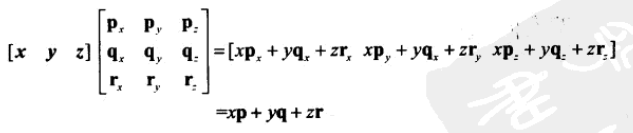
12、绕x、y、z 轴旋转 0度。

　　

　　记法诀窍：

　　1、斜角都是 cos0。

　　2、固定轴的下一个是 sin0。

　　3、固定轴的下下一个是 -sin0。

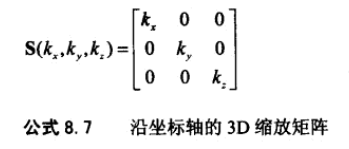
13、沿坐标轴的绽放矩阵。

　　

14、切变，切变后面积、体积不变。也被称作扭曲变换。以下是 2d切变矩阵：

　　

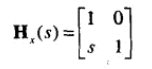
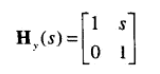
　　以下是3D切变矩阵。

　　

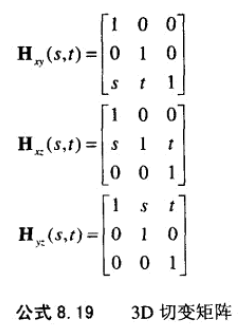
15、线性变换。满足加法、线性乘，那么叫线性变换。

　　

　　

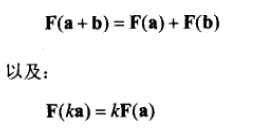
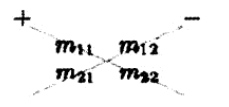
16、2 维行列式

　　

　　3维行列式：

　　

　　如果将矩阵解释为 abc 向量，那么矩阵的行列式可以写为：

　　

17、M{i,j} 称为 M的i行j列的余子式，意为去除i行j列后余下的矩阵。

　　

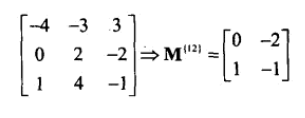
　　加上-/+后称为代数余子式。

　　

　　

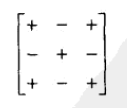
　　任一一行的代数余子式与元素乘积的和，即为行列式，所以这里得到行列式的另一个计算方法：

　　

　　

18、矩阵行列式的特性。

　　

19、2D中，行列式的值为基向量围成图形的面积。

　　

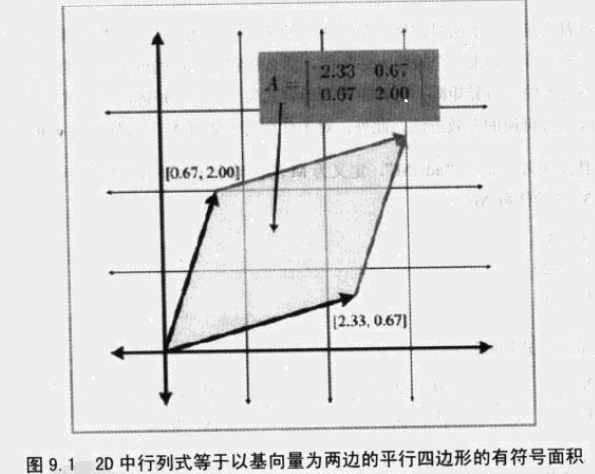
　　3D中，行列式等于基向量的体积。

20、如果一个矩阵有逆矩阵，则称它为可逆的或非奇异的（非单身）。如果没有逆矩阵，则为不可逆，奇异。

　　奇异矩阵的行列式为零，非奇异的行列式不为零。因为逆矩阵的计算需要除以行列式 |M|。

21、adj M 是标准伴随矩阵，是代数余子式矩阵的转置。

　　

　　

　　

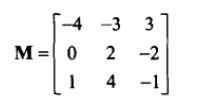
　　逆矩阵的计算公式：
　　

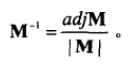
　　逆矩阵的特性：

　　

　　

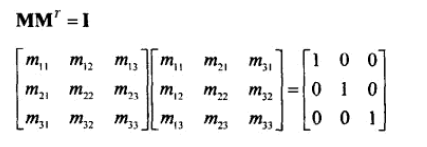
22、正交矩阵：M*M^T=I

　　如果一个矩阵是正交的，那么它的转置等于它的逆： M^-1 = M^T。

　　这是快速计算逆矩阵的一种常用方法。

23、正交矩阵性质的推导。

　　

　　

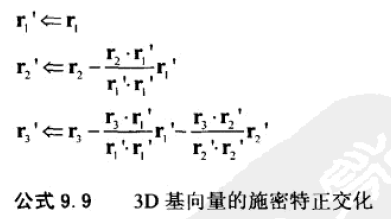
23.1、3D矩阵的施密特正交化。

　　　　

　　施密特正交化是有偏差的，一个例子是rq总是不变的。一个改进的算法是，选择一个小因子，迭代N次。

　　　　

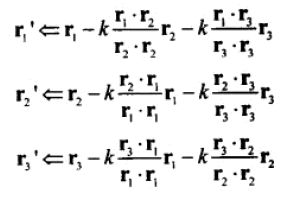
24、3D 平移矩阵。

　　

24.1、一般仿射变换。

　　

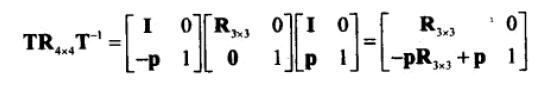
25、投影的计算。

　　　　

26、

27、

28、

29、

【3D中绕任意轴的旋转】

　　假设旋转轴通过原点，为n，旋转的角度为0。被旋转轴为 v，旋转后的轴为 v'。则我们需要找到的旋转矩阵R为：

　　　　

　　先构造空间，可以将 v 拆分为 v1、v2，v1平行n，v2垂直n。

　　　　　　

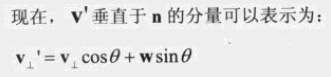
　　　　下面的等式可由两种方式得到：

　　　　1）0 的旋转矩阵。

　　　　2）水平分量、垂直分量相加。

　　　　

　　　　

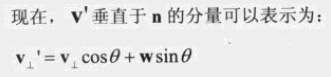
　　将 [1,0,0]、[0,1,0]、[0,0,1] 代入，即可得三个旋转后的坐标轴。

　　

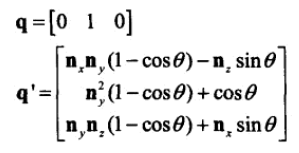
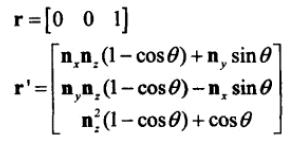
　　综合在一起，可得旋转矩阵：

　　　　

【沿任意方向缩放】

　　现在来解决，沿方向n，绽放k倍的问题。假设需要绽放轴 v，那么v可拆分为v1，v2。v1平行于 n，v2 垂直于n。

　　　　

　　

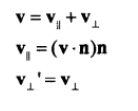
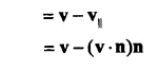
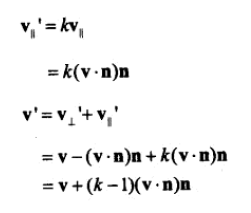
　　上式中，(VN)N 为 V||，再乘上 (k-1)，所以此公式的含意为给 V 加一个 (k-1)V|| 的偏移。

　　所以，三个轴旋转后分别为：

　　　　

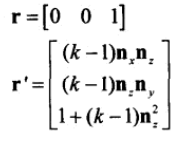
　　绽放矩阵为：

　　　　

　　有了上述公式后，可轻易的得出绕任意平面投影的矩阵：

　　　　　　

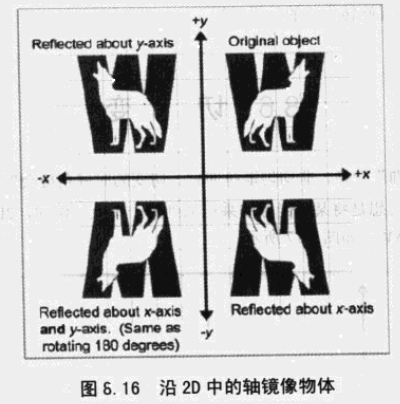
　　同样，镜像矩阵也很容易得出：