CodeForces 907E Party(bfs+状压DP)

Arseny likes to organize parties and invite people to it. However, not only friends come to his parties, but friends of his friends, friends of friends of his friends and so on. That's why some of Arseny's guests can be unknown to him. He decided to fix this issue using the following procedure.

At each step he selects one of his guests A, who pairwise introduces all of his friends to each other. After this action any two friends of Abecome friends. This process is run until all pairs of guests are friends.

Arseny doesn't want to spend much time doing it, so he wants to finish this process using the minimum number of steps. Help Arseny to do it.

Input

The first line contains two integers n and m (1 ≤ n ≤ 22; 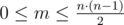) — the number of guests at the party (including Arseny) and the number of pairs of people which are friends.

Each of the next m lines contains two integers u and v (1 ≤ u, v ≤ n; u ≠ v), which means that people with numbers u and v are friends initially. It's guaranteed that each pair of friends is described not more than once and the graph of friendship is connected.

Output

In the first line print the minimum number of steps required to make all pairs of guests friends.

In the second line print the ids of guests, who are selected at each step.

If there are multiple solutions, you can output any of them.

Examples

input

Copy

5 6
1 2
1 3
2 3
2 5
3 4
4 5

output

Copy

2
2 3 

input

Copy

4 4
1 2
1 3
1 4
3 4

output

Copy

1
1 

Note

In the first test case there is no guest who is friend of all other guests, so at least two steps are required to perform the task. After second guest pairwise introduces all his friends, only pairs of guests (4, 1) and (4, 2) are not friends. Guest 3 or 5 can introduce them.

In the second test case guest number 1 is a friend of all guests, so he can pairwise introduce all guests in one step.

题意:给出n个人和他们之间的友谊关系,每次可以让一个人的所有朋友都认识,求最少要选出几个人才能让所有人都互相认识?(有先后顺序)并且输出方案

题解:这道题一开始想到的是zz无脑状压,结果有不能保证一定正解,接着想到了之前某场bfs式的状压,然后就过了,方案什么的写个栈记录一下就行了,dfs什么的也是可以做的,但是不如bfs直接啦~

代码如下:

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int f[(<<)+],pre[(<<)+],key[(<<)+];
int a[],ans[],cnt,n,m;
queue<int> q;

void bfs()
{
    memset(f,,sizeof(f));
    memset(key,-,sizeof(key));
    memset(pre,-,sizeof(pre));
    for(int i=;i<n;i++)
    {
        f[a[i]]=;
        key[a[i]]=i;
        q.push(a[i]);
    }
    int now,tmp;
    while(!q.empty())
    {
        now=q.front();
        q.pop();
        for(int i=;i<n;i++)
        {
            if(now&(<<i))
            {
                tmp=now|a[i];
                if(!f[tmp])
                {
                    f[tmp]=f[now]+;
                    key[tmp]=i;
                    pre[tmp]=now;
                    q.push(tmp);
                    if(tmp==((<<n)-))
                    {
                        return ;
                    }
                }
            }
        }
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    int from,to;
    for(int i=;i<n;i++)
    {
        a[i]|=(<<i);
    }
    for(int i=;i<=m;i++)
    {
        scanf("%d%d",&from,&to);
        from--;to--;
        a[from]|=(<<to);
        a[to]|=(<<from);
    }
    if(m==n*(n-)/)
    {
        puts("");
        return ;
    }
    bfs();
    cnt=;
    int now=(<<n)-;
    while(~now)
    {
        ans[++cnt]=key[now];
        now=pre[now];
    }
    printf("%d\n",cnt);
    while(cnt)
    {
        printf("%d",ans[cnt--]+);
        if(cnt)
            printf(" ");
        else
            printf("\n");
    }
}