Kmp算法浅谈

Kmp算法浅谈

一.Kmp算法思想

在主串和模式串进行匹配时，利用next数组不改变主串的匹配指针而是改变模式串的匹配指针，减少大量的重复匹配时间。在Kmp算法中，next数组的构建是整个Kmp算法的核心所在。

二.Kmp核心之next数组的构建

（1）前缀，后缀的定义

（2）最长公共前后缀定义

（3）next数组的含义

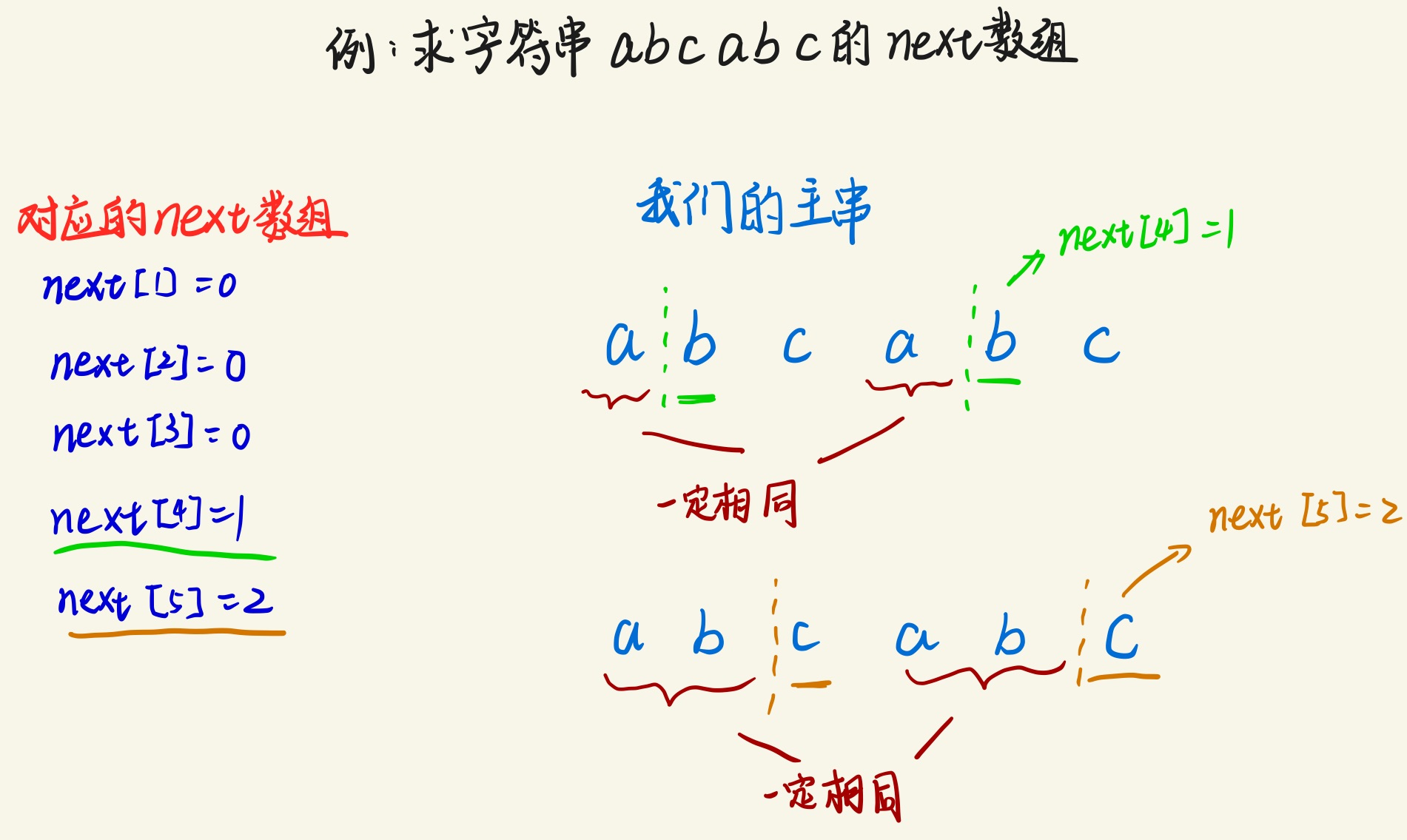
next数组代表各个长度子串(这些字串的起始位置都为0)的最长公共前后缀长度，为了方便代码的编写next[0]定为-1，表示前0个字符根本不存在前后缀这一说法。其他的例如next[1]表示前一个字符的 最长公共前后缀 ，很明显根据前后缀的定义，next[1]=0;next[1]和next[0]在本博客说明的next数组构成中是唯一和确定的。

（4）最长公共前后缀定义及与next的联系

（5）对于一个模式串next数组到底能表示什么

首先根据上面的说法next数组表示了模式串长度为i的前缀的最长公共前后缀的的长度，所以说next可以来表示长度。这个时候我们在深究一下它表示的是谁的长度？它表示的是最长公共前后缀的!!!!,也就是说它可以表示模式串中第next[i]个元素的下标!!!,不懂的话看图就明白了

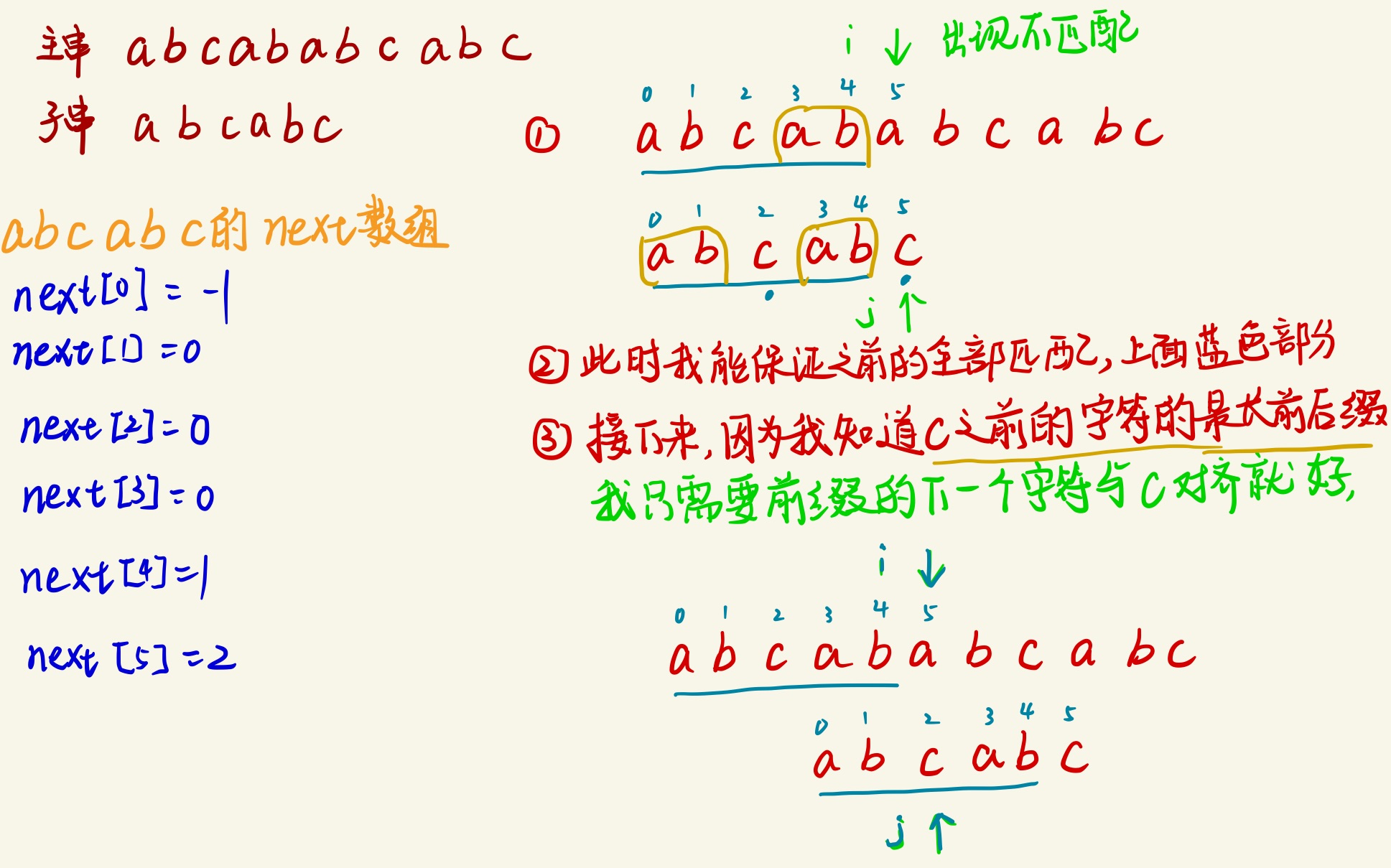
（6）如何利用next数组的性质避免重复匹配呢

三.如何用代码的形式得到next数组

首先上个代码

void Getnext(int next[],char *MyString)
{
   int j=,k=-;
   next[]=-;//规定，方便后面k的计算
   while(j<strlen(MyString)-)//j不能超过整个串的长度
   {
      //j为当前字符,k为j前面那些字符的最长公共前后缀的下一个字符
      if(k == - || MyString[j] == MyString[k])next[++j] = ++k;
      //模式串的第一个字符就要比较的字符不一样,那我就要将模式串的下一个字符和我要比较的字符比较，且现在k还是为-1的，所以++j,++k
      else k = next[k];
   }
}

三.Kmp算法代码

得到了next后一切就简单了，无非就是设定两个“指针”分别指向主串和模式串，当出现不匹配时模式串的指针根据next数组移动就好了，直接上代码

int Kmp(char *T,int numt,char *P,int nump,int *next)//T为主串，P为模式串
{
    int i=,j=;//i为主串的指针，j为模式串的指针
    while(i<=numt-nump)
    {
        while((T[i]==P[j]&&i<numt)||j==-) ++i,++j;//j==-1
//模式串第一个就和主串中要匹配的字符不匹配，主串字符后移一位，模式串的指针也从-1恢复到零
        if(j==nump)//找到匹配串
        return i-nump;//返回在主串中的起始位置
        j=next[j];
    }
    return -;//表示无法找到
}

四.整个程序完整代码

#include <stdio.h>
#include <string.h>
void Getnext(int next[],char *MyString);
int Kmp(char *T,int numt,char *P,int nump,int *next);
const int SIZE=;
int main()
{
    char *T=new char[SIZE];
    char *P=new char [SIZE];
    int *next=new int [SIZE];
    scanf("%s",T);
    scanf("%s",P);
    Getnext(next,P);
    for(int i=;i<strlen(P);i++) printf("%d,",next[i]);
    printf("\n%d",Kmp(T,strlen(T),P,strlen(P),next));
    return ;
}
void Getnext(int next[],char *MyString)
{
   int j=,k=-;
   next[]=-;
   while(j<strlen(MyString)-)
   {
      if(k == - || MyString[j] == MyString[k])next[++j] = ++k;
      else k = next[k];
   }
}
int Kmp(char *T,int numt,char *P,int nump,int *next)//T为主串，P为模式串
{
    int i=,j=;//i为主串的指针，j为模式串的指针
    while(i<=numt-nump)
    {
        while((T[i]==P[j]&&i<numt)||j==-) ++i,++j;
        if(j==nump)//找到匹配串
        return i-nump;//返回在主串中的起始位置
        j=next[j];
    }
    return -;//表示无法找到
}