改善深层神经网络（三）超参数调试、Batch正则化和程序框架

1、超参数调试：

（1）超参数寻找策略：

对于所有超参数遍历求最优参数不可取，因为超参数的个数可能很多，可选的数据过于庞大.

由于最优参数周围的参数也可能比较好，所以可取的方法是：在一定的尺度范围内随机取值，先寻找一个较好的参数，再在该参数所在的区域更精细的寻找最优参数.

（2）选择合适的超参数范围：

假设 n^[l] 可选取值 50~100：在整个范围内随机均匀取值

选取神经网络层数 #layers，L的可选取值为 2~4：在整个范围内随机均匀取值

学习速率 α 的可选取值 0.0001~1：在对数轴上随机均匀取值

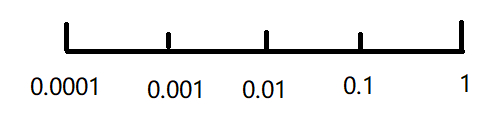
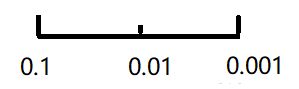
β 的可选取值 0.9~0.999：在 1-β 的对数轴上随机均匀取值

　 

2、Batch归一化：

（1）问题背景：

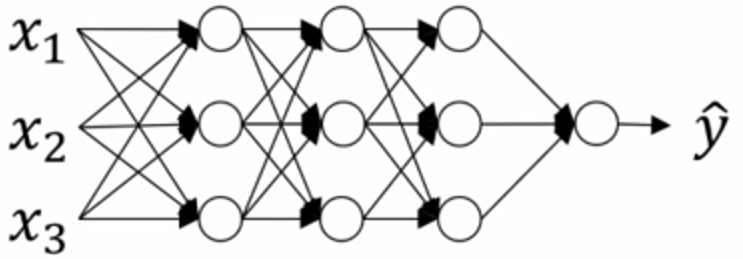
　　　　   a^[1]     a^[2]      a^[3]

之前介绍的正则化输入是对 X 进行正则化，那么能否对 a^[2] 进行正则化（本质是对 z^[2] 正则化），以更快地训练 w^[3] 和 b^[3] ?

（2）Batch归一化流程：

给出参数：Z⁽¹⁾ ... Z^(m)

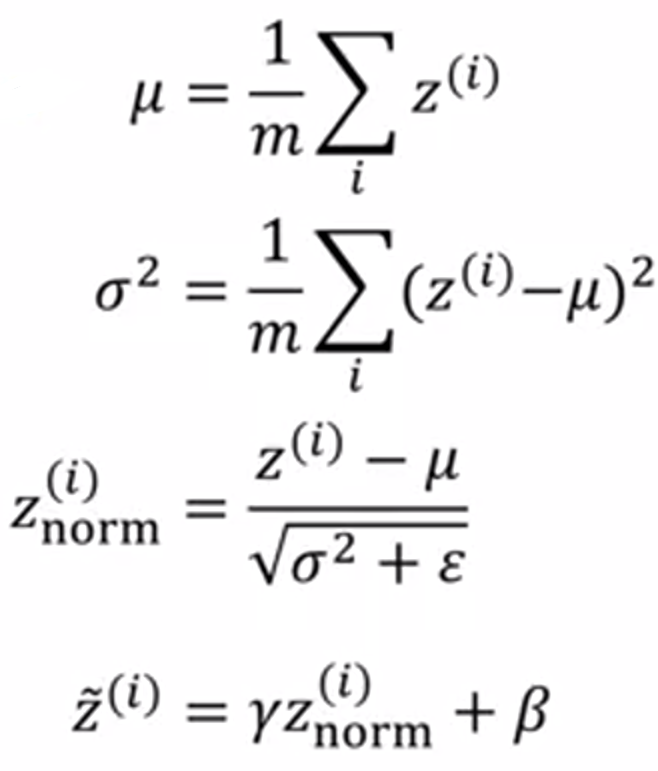
其中 γ 和 β 为学习参数，作用是：可以随意设置 Z^~(i) 的平均值和方差.

传播过程：

X — _w^[1],b^[1] —> Z^[1] — _{γ^[1], β^[1]} —> Z^~[1] —_g(Z^~[1]) —> A^[1] — _w^[2],b^[2] —> Z^[2] — ... —> Y^

需要优化的参数：

W^[1], b^[1], ..., W^[L], b^[L]

γ^[1], β^[1], ..., γ^[L], β^[L]

一个小的简化：

由于在计算 Z^~(i) 前会通过正则化把均值设成0，那么参数 b 可以不用加上.

（3）应用：

for t = 1 ... num_MiniBatches:

　　Compute forward prop on X^{t}

　　In each hidden layer，use Batch Norm to replace Z^[l] with Z^~[l]

　　Use backprop to compute dW^[l], dβ^[l], dγ^[l]

　　Update parameters W^[l], β^[l], γ^[l]

(Work with momentum、RMSprop、Adam)

3、Softmax回归：

（1）举例说明：

Softmax回归适用于多类别分类，以4分类为例：

神经网络模型：

假设 Z[L] = [5, 2, -1, 3]^T

t = [e⁵, e², e^-1, e³]^T ≈ [148.4, 7.4, 0.4, 20.1]^T

∑ t = 176.3

a^[L] = t / ∑ t = [0.842, 0.042, 0.002, 0.114]^T

即是分类0的概率是0.842，分类1的概率是0.042，分类2的概率是0.002，分类3的概率是0.114.

（2）Softmax分类器损失函数：

训练结果集：Y = [y⁽¹⁾, y⁽²⁾, ..., y^(m)]，每一个 y(i) 都是一个列向量.

预测结果集：Y^ = [y^⁽¹⁾, y^⁽²⁾, ..., y^^(m)]

单个训练样本的损失函数： L(y^, y) = - ∑ y_j * log(y^_j)

整个训练集的损失函数：J(w^[1], b^[1], ...) = 1 / m * ∑ L(y^⁽ⁱ⁾, y⁽ⁱ⁾)

4、TensorFlow使用举例：

最小化 J = (w - 5)² = w² - 10w + 25:

（1）写法①：

w = tf.Variable(0, dtype = tf.float32)

cost = tf.add(tf.add(w**2, tf.multiply(-10, w)), 25)

train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

init = tf.global_variables_initializer()

session = tf.Session()

session.run(init)

print(session.run(w))

#输出0.0

for i in range(1000):

　　session.run(train)

print(session.run(w))

#输出4.99999

（2）写法②：

coefficients = np.array([[1.], [-10.], [25.]])

w = tf.Variable(0, dtype = tf.float32)

x = tf.placeholder(tf.float32, [3,1])

cost = x[0][0]*w**2 + x[1][0]*w + x[2][0]

train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

init = tf.global_variables_initializer()

session = tf.Session()

session.run(init)

print(session.run(w))

#输出0.0

for i in range(1000):

　　session.run(train, feed_dicts(x:coefficients))

print(session.run(w))

#输出4.99999