CGMH:Constrained Sentence Generation by Metropolis-Hastings Sampling解读

根据关键字生成句子：

读进关键字，随机选择处理手段（增删改）以及待处理word的位置，然后计算接受/拒绝概率，根据概率生成一个新的序列，再循环这一过程，循环次数是500，每次都将困惑度最低的生成句子放在列表中第一个位置，最后根据config设置的最短长度（如7），当列表中的一个句子长度大于7时，则将该句子输出，作为最终生成的句子。

其中，计算接受/拒绝概率的方法：

先计算一个句子的固定分布：（=语言模型中该句的概率*关键字的指示函数）

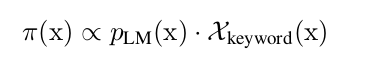
再计算某个token被接受的概率：

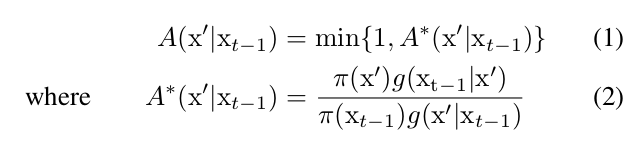
论文翻译：

1.MH采样的框架：包括建议设计，固定分布，接受决定

1）温和条件下，样本得分不会瘦脸为马尔科夫链的固定分布。所以，目的是设计一个马尔科夫链，其固定分布是想要的句子分布。

首先，MH采样器分两步解决这个问题：一是提出一个实验性转换，根据接受率来接受或者拒绝一个建议。接受/拒绝率通过想要的固定分布和建议的固定分布来计算，这确保了细节平衡条件，该条件保证MH收敛到想要的分布。

让 π(x)表示我们想要从中取样的句子的分布（x表示一个特定的句子）。MH从任意状态x0开始（一个出示句子或 一系列关键字），在每个步骤t,根据建议的分布g(x’|x_t-1),提出一个新的句子x‘,其中x_t-1表示最后一步的句子。

根

根据概率1-A,一个建议应该被拒绝，则x_t = x_t-1。理论上，对于一个不可再分的且非周期性的马尔科夫链来说，当n趋于无穷时，样本x_n的分布会收敛到π(x)。实际上，初始的几个样本会被丢弃。如果样本收敛到固定分布，则该马尔科夫链建立完成。

2）

2.根据关键字生成句子实验

使用500万句子训练出一个语言模型，使用该语言模型训练CGMH模型

输入：使用3000个句子提供关键字，用来测试。对于每个句子，随机采样一个或者多个words作为限制条件。

输出：对于MH采样，我们使用关键字序列作为初始状态，然后选择100步后有最低困惑度（即流畅度最高）的语句作为输出。