dp练习（7）—— 最小和

3415 最小和

CodeVS原创

 时间限制: 1 s

 空间限制: 64000 KB

 题目等级 : 青铜 Bronze

题解

 

 

 

题目描述 Description

小浣熊松松来到文具店，选择了K支自己喜欢的水彩笔，并抄下了它们的价格。可是到结算时，他发现自己抄价格时抄得太密集，以至于所有价格连成了一个数字串（你可以假设价格都是正整数）。老板想和松松开个玩笑，于是对他说：“你可以把这个数字串分成K段，代表这K支笔的价格，然后把他们加起来，就是你要付给我的钱了。”当然，松松想尽可能省下钱去买《算法导论》，所以请你来帮忙算算，他最少需要付多少钱。

输入描述 Input Description

第一行包含一个整数N，代表松松抄下来的数字串。

第二行包含一个整数K，代表松松买了K支水彩笔。

输出描述 Output Description

输出仅一行，为松松买这些笔最少花的钱。

样例输入 Sample Input

79846

3

样例输出 Sample Output

133

先贴上代码：

#include<bits/stdc++.h>
using namespace std;

char N[];
int k;
long long dp[][];
long long Count(int h,int i)
{
    long long sum = ;
    for(int j=h-;j < i;j++)
    {
        sum = sum *  + (N[j] - '') ;
    }
    return sum;

}
int main()
{
    cin >> N >> k;
    memset(dp,INT8_MAX,sizeof(dp));
    for(int i=;i <= strlen(N);i++)
    {
        dp[i][] = Count(,i);
//        cout << dp[i][0] << endl;
    }
    for(int h=;h <= k;h++) //h个乘号
    {
        for(int i=;i <= strlen(N);i++)//到第i个数字
        {
            for(int j=;j <= i;j++)//1~i之间走动的j
            {
                dp[i][h] = min(dp[i][h],dp[j][h-] + Count(j+,i));
            }
        }
    }
    cout << dp[strlen(N)][k-] << endl;
//    for(int i=0;i < 6;i++)
//    {
//        for(int j=0;j < 6;j++)
//            cout << dp[i][j] << " ";
//        cout << endl;
//    }

    return ;
}

代码分析

要搞懂这段代码首先要明白数组的含义

h 代表的是有几个加号 ， i 与 j 是经典动态规划里的东西 i 从1~n，j从1~i；

那个函数的作用是把字符串拆分，执行第一处的测试输出得：

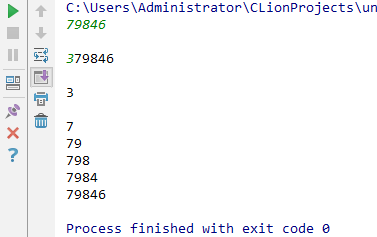
（结合实例应该比较好理解）

然后，是最重要的三个循坏：

for(int h=;h <= k;h++) //h个乘号
    {
        for(int i=;i <= strlen(N);i++)//到第i个数字
        {
            for(int j=;j <= i;j++)//1~i之间走动的j
            {
                dp[i][h] = min(dp[i][h],dp[j][h-] + Count(j+,i));
            }
        }
    }

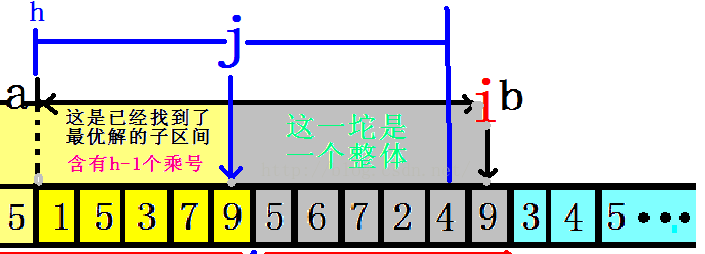
借用了别人的图片来解释：

dp[i][h] = min(dp[i][h],dp[j][h-1] + Count(j+1,i));
dp[i][h]到第i个用了h个加号，dp[j][h-1] + Count(j+1,i) 就是上面这幅图的代码表示　　

测试结果，测试输出dp[][]：

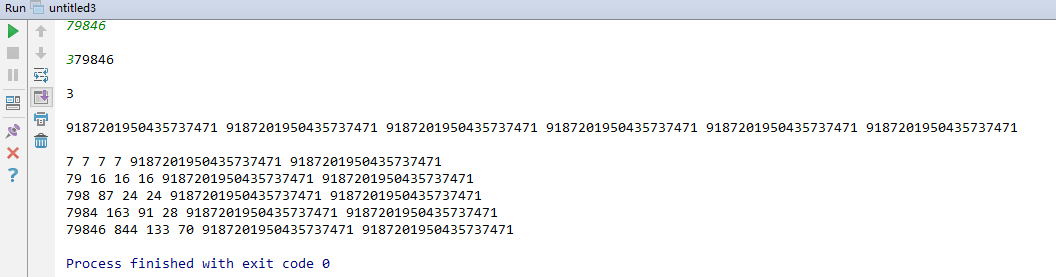
最后得到133
（ps：有个注意点就是用min求最小值的时候要将数组初始化为INTMAX）