bp算法中为什么会产生梯度消失？

作者：维吉特伯
链接：https://www.zhihu.com/question/49812013/answer/148825073
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

简单地说，根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话（ $w_{ij}y_{i}'<1.0$ ），那么即使这个结果是0.99，在经过足够多层传播之后，误差对输入层的偏导会趋于0（ $\lim_{n\to\infty}0.99^n=0$ ）。下面是数学推导推导。

假设网络输出层中的第 $k$ 个神经元输出为 $y_{k}(t)$ ，而要学习的目标为 $d_{k}(t)$ 。这里的 $t$ 表示时序，与输入无关，可以理解为网络的第 $t$ 层。

&lt;img src="https://pic2.zhimg.com/50/v2-2fae1a385c8dcada16e17799fa175711_hd.png" data-rawwidth="560" data-rawheight="397" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic2.zhimg.com/v2-2fae1a385c8dcada16e17799fa175711_r.png"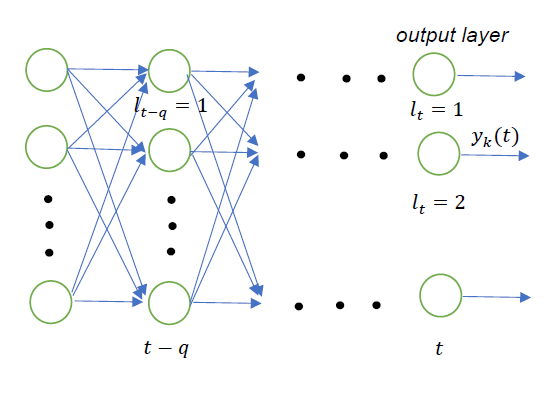&gt;

若采用平方误差作为损失函数，第 $k$ 个输出神经元对应的损失为 $L=\frac{1}{2}(d_{k}(t)-y_{k}(t))^{2}$

将损失 $L$ 对输出 $y_{k}(t)$ 求偏导 $\vartheta_{k}(t)=\frac{\partial{L}}{\partial{y_{k}(t)}}=y_{k}'(t)(d_{k}(t)-y_{k}(t))$

根据链式法则，我们知道，第 $t-1$ 层的梯度可以根据第 $t$ 层的梯度求出来

$\vartheta_{i}(t-1)=y_{i}'(t-1)\sum_{j}w_{ij}\vartheta_{j}(t)$

这里用 $i$ 表示第 $t-1$ 层的第 $i$ 个神经元， $j$ 表示第 $t$ 层的第 $j$ 个神经元。

进一步，第 $t-q$ 层的梯度可以由第 $t-q+1$ 层的梯度计算出来

$\vartheta_{i}(t-q)=y_{i}'(t-q)\sum_{j}w_{ij}\vartheta_{j}(t-q+1)$

这实际上是一个递归嵌套的式子，如果我们对 $\vartheta_{j}(t-q+1)$ 做进一步展开，可以得到式子

$\vartheta_{i}(t-q)=y_{i}'(t-q)\sum_{j}w_{ij}[y_{j}'(t-q+1)\sum_{k}w_{jk}\vartheta_{k}(t-q+2))]$

最终，可以一直展开到第 $t$ 层。

把所有的加法都移到最外层，可以得到

$\vartheta_{i}(t-q)=\sum_{l_{t-q+1}=1}^{n}\cdot\cdot\cdot\sum_{l_{t}=1}^{n}\prod_{m=0}^{q}w_{l_{m}l_{m-1}}\vartheta_{lm}(t-m)$

$l_{t-q+1}$ 表示的是第 $t-q+1$ 层中神经元的下标（即第 $t-q+1$ 层第 $l_{t-q+1}$ 个神经元）， $l_{t}$ 表示第 $t$ 层的下标。 $m=0$ 对应输出层， $m=q$ 对应第 $t-q$ 层。实际上展开式就是从网络的第 $t$ 层到 $t-q$ 层，每一层都取出一个神经元来进行排列组合的结果。这个式子并不准确，因为 $m=0$ 时实际是损失 $L$ 对输出层的偏导，即

$\vartheta_{k}(t)=y_{k}'(t)(d_{k}(t)-y_{k}(t))$ ，

并没有应用权重 $w_{l_{m}l_{m-1}}$ ，把它修正一下

$\vartheta_{i}(t-q)=\sum_{l_{t-q+1}=1}^{n}\cdot\cdot\cdot\sum_{l_{t}=1}^{n}\prod_{m=1}^{q}w_{l_{m}l_{m-1}}y_{lm}'(t-m)\cdot\vartheta_{k}(t)$

这样，我们就得到了第 $t-q$ 层和第 $t$ 层的梯度之间的关系

$\frac{\vartheta_{i}(t-q)}{\vartheta_{k}(t)}=\sum_{l_{t-q+1}=1}^{n}\cdot\cdot\cdot\sum_{l_{t}=1}^{n}\prod_{m=1}^{q}w_{l_{m}l_{m-1}}y_{lm}'(t-m)$

在上面的式子中，由于加法项正负号之间可能互相抵消。因此，比值的量级主要受最后的乘法项影响。如果对于所有的 $m$ 有

$|w_{l_{m}l_{m-1}}y_{lm}'(t-m)|>1.0$

则梯度会随着反向传播层数的增加而呈指数增长，导致梯度爆炸。

如果对于所有的 $m$ 有

$|w_{l_{m}l_{m-1}}y_{lm}'(t-m)|<1.0$

则在经过多层的传播后，梯度会趋向于0，导致梯度消失。

LSTM就是为了解决以上两个问题提出的方法之一，它强制令 $w_{l_{m}l_{m-1}}y_{lm}'(t-m)=1.0$ 。 LSTM如何来避免梯度弥撒和梯度爆炸？ - 知乎

有兴趣可以参考Long Short Term Memory 一文。上面的推导过程大体上也参考自这篇论文。

Reference：

Graves, Alex. Long Short-Term Memory. Supervised Sequence Labelling with Recurrent Neural Networks. Springer Berlin Heidelberg, 2012:1735-1780.

bp算法中为什么会产生梯度消失？的更多相关文章

关于BP算法在DNN中本质问题的几点随笔 [原创 by 白明] 微信号matthew-bai
随着deep learning的火爆,神经网络(NN)被大家广泛研究使用.但是大部分RD对BP在NN中本质不甚清楚,对于为什这么使用以及国外大牛们是什么原因会想到用dropout/sigmoid ...
今天开始学Pattern Recognition and Machine Learning (PRML)，章节5.2-5.3，Neural Networks神经网络训练（BP算法）
转载请注明出处:http://www.cnblogs.com/xbinworld/p/4265530.html 这一篇是整个第五章的精华了,会重点介绍一下Neural Networks的训练方法——反 ...
梯度消失&&梯度爆炸
转载自: https://blog.csdn.net/qq_25737169/article/details/78847691 前言本文主要深入介绍深度学习中的梯度消失和梯度爆炸的问题以及解决方案. ...
LSTM及其变种及其克服梯度消失
本宝宝又转了一篇博文,但是真的很好懂啊: 写在前面:知乎上关于lstm能够解决梯度消失的问题的原因: 上面说到,LSTM 是为了解决 RNN 的 Gradient Vanish 的问题所提出的.关于 ...
DNN的BP算法Python简单实现
BP算法是神经网络的基础,也是最重要的部分.由于误差反向传播的过程中,可能会出现梯度消失或者爆炸,所以需要调整损失函数.在LSTM中,通过sigmoid来实现三个门来解决记忆问题,用tensorflo ...
神经网络误差逆传播算法推导 BP算法
误差逆传播算法是迄今最成功的神经网络学习算法,现实任务中使用神经网络时,大多使用BP算法进行训练. 给定训练集\(D={(x_1,y_1),(x_2,y_2),......(x_m,y_m)} ...
机器学习 —— 基础整理（八）循环神经网络的BPTT算法步骤整理；梯度消失与梯度爆炸
网上有很多Simple RNN的BPTT(Backpropagation through time,随时间反向传播)算法推导.下面用自己的记号整理一下. 我之前有个习惯是用下标表示样本序号,这里不能再 ...
神经网络中 BP 算法的原理与 Python 实现源码解析
最近这段时间系统性的学习了 BP 算法后写下了这篇学习笔记,因为能力有限,若有明显错误,还请指正. 什么是梯度下降和链式求导法则假设我们有一个函数 J(w),如下图所示. 梯度下降示意图现在,我们 ...
Recurrent Neural Network系列3--理解RNN的BPTT算法和梯度消失
作者:zhbzz2007 出处:http://www.cnblogs.com/zhbzz2007 欢迎转载,也请保留这段声明.谢谢! 这是RNN教程的第三部分. 在前面的教程中,我们从头实现了一个循环 ...

随机推荐

mysql分页查询优化(索引延迟关联)
对于web后台报表导出是一种常见的功能点,实际对应服务后端即数据库的排序分页查询.如下示例为公司商户积分报表导出其中一个sql ,当大批量的导出请求进入时候,mysql的cpu急剧上升瞬间有拖垮库的风 ...
CentOS下多网卡绑定多IP段时导致只有一个会通的问题解决
原因:Linux默认开启了反向路由检查导致的,比如说外面访问eth0的网卡,而网关在eth1上,又或者从eth0出的流量,而网关在eth1上,此时会检查到网关不在同一个网卡上导致出不去,进不来的问题. ...
Sed&awk笔记之sed篇(转)
Sed是什么 <sed and awk>一书中(1.2 A Stream Editor)是这样解释的: Sed is a "non-interactive" strea ...
MyEclipse使用总结——设置MyEclipse使用的Tomcat服务器
一.设置使用的Tomcat服务器如果不想使用MyEclipse自带的tomcat服务器版本,那么可以在MyEclipse中设置我们自己安装好的tomcat服务器设置步骤如下: Window→Pre ...
Delphi XE5 Android 运行黑屏卡死的解决方法
1. 确保正确安装Android SDK: 开始菜单 > 所有程序 > Embarcadero RAD Studio XE5 > > Android Tools > 打开 ...
ios（包括6、7）应用程序引用系统通讯录的方法［亲测可行］
由于ios系统对用户隐私的控制,第三方应用程序只能通过苹果官方接口调用系统通讯录,不能像android那样直接操作通讯录数据库. 一般地,使用系统自带通讯录的方法有两种,一种是直接将整个通讯录 ...
手工Ghost安装系统
(1)其实手工ghost很简单,正确操作的话是不会有什么问题的,在PE下,打开ghost程序 (2)按任意键进入ghost操作界面,出现ghost菜单,我们现在只用到Local菜单项,下面有三个子项: ...
IllegalStateException: Can not perform this action after onSaveInstanceState
http://www.cnblogs.com/zgz345/archive/2013/03/04/2942553.html 今天使用Fragment的时候,出现了这个错误 IllegalStateEx ...
错误：update 忘了加 where
职业生涯应该都犯过的错误,幸好是在开发库,生产环境的库真是要严格的进行权限管理和脚本执行流程规范.
docker 日志清理与设置
清空 cat /dev/null >json.log docker-compose nginx: image: nginx:1.12.1 restart: always logging: dri ...

bp算法中为什么会产生梯度消失？

bp算法中为什么会产生梯度消失？的更多相关文章

随机推荐

热门专题