POJ 2976 二分

Dropping tests

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 12515		Accepted: 4387

Description

In a certain course, you take n tests. If you get a_i out of b_i questions correct on test i, your cumulative average is defined to be

.

Given your test scores and a positive integer k, determine how high you can make your cumulative average if you are allowed to drop any k of your test scores.

Suppose you take 3 tests with scores of 5/5, 0/1, and 2/6. Without dropping any tests, your cumulative average is . However, if you drop the third test, your cumulative average becomes .

Input

The input test file will contain multiple test cases, each containing exactly three lines. The first line contains two integers, 1 ≤ n ≤ 1000 and 0 ≤ k < n. The second line contains n integers indicating a_i for all i. The third line contains n positive integers indicating b_i for all i. It is guaranteed that 0 ≤ a_i ≤ b_i ≤ 1, 000, 000, 000. The end-of-file is marked by a test case with n = k = 0 and should not be processed.

Output

For each test case, write a single line with the highest cumulative average possible after dropping k of the given test scores. The average should be rounded to the nearest integer.

Sample Input

3 1
5 0 2
5 1 6
4 2
1 2 7 9
5 6 7 9
0 0

Sample Output

83
100

Hint

To avoid ambiguities due to rounding errors, the judge tests have been constructed so that all answers are at least 0.001 away from a decision boundary (i.e., you can assume that the average is never 83.4997).

Source

Stanford Local 2005

题意：

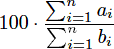有n门课，每门课有一个总分值b和我的得分a，我的总成绩是 ，在能去掉k门课的情况下，求我能得到的最大成绩。

代码：

//和上一题一样。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
const double esp=0.000001;
int n,k;
double x;
struct Lu{
    double a,b;
    bool operator < (const Lu &p)const{
        return a-x*b>p.a-x*p.b;
    }
}L[maxn];
bool solve(double m){
    x=m;
    sort(L,L+n);
    double tmp1=,tmp2=;
    for(int i=;i<n-k;i++){
        tmp1+=L[i].a;
        tmp2+=L[i].b;
    }
    return tmp1-m*tmp2>=;
}
int main()
{
    while(scanf("%d%d",&n,&k)==&&(n+k)){
        for(int i=;i<n;i++) scanf("%lf",&L[i].a);
        for(int i=;i<n;i++) scanf("%lf",&L[i].b);
        double l=,r=,ans;
        while(r-l>esp){
            double m=(l+r)/2.0;
            if(solve(m)){
                l=m;
            }else r=m;
        }
        printf("%.0lf\n",l*);
    }
    return ;
}