Codeforces 932G Palindrome Partition - 回文树 - 动态规划

题目传送门

　　通往???的传送点

　　通往神秘地带的传送点

　　通往未知地带的传送点

题目大意

　　给定一个串$s$，要求将$s$划分为$t_{1}t_{2}\cdots t_{k}$，其中$2\mid k$，且$t_{i} = t_{k - i}$，问方案数。

　　直接做不太好做。虽然可以$O(n^{2})$进行动态规划。

　　考虑做一步转化：设$s' = s_{1}s_{n}s_{2}s_{n - 1}\cdots s_{n / 2}s_{n / 2 + 1}$。

　　然后它的一个偶回文划分可以和原来的划分一一对应。

　　于是可以$O(n^{2})$进行动态规划。然后完美TLE。

定理1 一个回文的后缀是回文串当且仅当它是原串的border。

　　根据回文串和border的定义容易证明。

引理1 （Weak Periodicity Lemma） 设$p$和$q$是$s$的周期，且$p + q \leqslant |s|$，则$(p, q)$也是$s$的周期

　　证明 不妨设$p < q, d = q - p$。

• 当$|s| - q\leqslant i \leqslant |s| - d$时，$s_{i} = s_{i - p} = s_{i - p + q} = s_{i + d}$
• 当$1\leqslant i < |s| - q$时，$s_{i} = s_{i + q} = s_{i + q - p} = s_{i + d}$。

　　然后根据辗转相除法能够得到$(p, q)$也是$s$的周期。因此定理得证。

引理2 字符串的所有长度不小于$|s| / 2$的所有border的长度构成等差数列。

　　证明 设$|s| - p (p\leqslant |s| / 2)$是$s$最长的$border$，另外某个border的长度是：$|s| - q (q\leqslant |s| / 2)$，那么能够推出$(p, q)$是$s$的周期，因此$|s| -  (p, q)$也是字符串$s$的border。由$p$的最小性以及$(p, q)\leqslant p$可知$(p, q) = p$，即$p\mid q$。

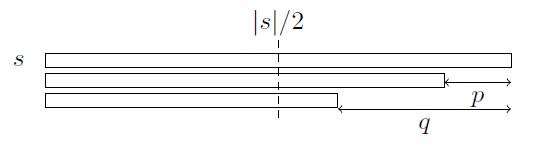
　　（懒得画图了，直接截论文的图）

　　不难证明对于任意$q (q\leqslant |s| / 2)$，且$p\mid q$的后缀是字符串$s$的border。

推论 一个字符串的border可以被分为不超过$\left \lceil log_{2}n  \right \rceil$段等差数列。

　　证明 设$2^{k}\leqslant n < 2^{k + 1}$，考虑以下几段的border：

$\begin{matrix}[2^{k}, n]\\ [2^{k - 1}, s^{k})\\ [2^{k - 2}, 2^{k - 1})\\ \vdots \\ [1, 2)\end{matrix}$

　　根据引理2可得长度属于每一段的border都是一个等差数列。

　　因此得证。

　　有了这个推论有什么用呢？

　　对于每一类border，每一次它被成为当前前缀的border意味着当前串的长度减去周期后，这些border还被发现了一次。

　　如上图，每次如果能够预处理出橙色部分，转移的时候只用补上没有计算的一项就好了.

　　用$f[i]$表示第$i$个前缀的偶回文划分的方案数。

　　用$g[i]$表示在回文树的状态$i$作为等差数列末项的时候等差border的动态规划的值的和。

　　建回文树的时候记一下dif和slink就可知道等差数列的差以及上一类等差数列的末项。

Code

 /**
  * Codeforces
  * Problem#932G
  * Accepted
  * Time: 93ms
  * Memory: 128200k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;

 const int alpha = ;

 typedef class TrieNode {
     public:
         int len, dif, g;
         TrieNode *ch[alpha];
         TrieNode *fail, *slink;
 }TrieNode;

 typedef class PalindromeTree {
     public:
         int len;
         TrieNode *pool;
         TrieNode *top;
         TrieNode *odd, *even;
         TrieNode *last;
         char *str; 

         TrieNode* newnode(int len) {
             top->len = len, top->dif = -, top->g = ;
             memset(top->ch, , sizeof(top->ch));
             top->fail = top->slink = NULL;
             return top++;
         }

         PalindromeTree() {        }
         PalindromeTree(int n) {
             pool = new TrieNode[(n + )];
             str = new char[(n + )];
             top = pool, len = ;
             odd = newnode(-), even = newnode();
             odd->fail = odd, even->fail = odd;
             odd->dif = even->dif = -, last = even, str[] = ;
         }

         TrieNode* extend(TrieNode* p) {
             while (str[len - p->len - ] != str[len])    p = p->fail;
             return p;
         }

         void append(char x) {
             str[++len] = x;
             int c = x - 'a';
             last = extend(last);
             if (!last->ch[c]) {
                 TrieNode* p = newnode(last->len + );
                 p->fail = extend(last->fail)->ch[c];
                 if (!p->fail)
                     p->fail = even;
                 last->ch[c] = p;
                 p->dif = p->len - p->fail->len; 

                 if (p->dif == p->fail->dif)
                     p->slink = p->fail->slink;
                 else
                     p->slink = p->fail;
             }
             last = last->ch[c];
         }
 }PalindromeTree;

 const int M = 1e9 + ;

 int n;
 char bstr[], str[];
 PalindromeTree pt;
 int *f;

 inline void init() {
     gets(bstr + );
     n = strlen(bstr + );
     for (int i = ; i <= n; i++) {
         if (i & )
             str[i] = bstr[(i + ) >> ];
         else
             str[i] = bstr[n - (i >> ) + ];
     }
     f = new int[(n + )];
     memset(f, , sizeof(int) * (n + ));
 }

 inline void solve() {
     pt = PalindromeTree(n);
     f[] = ;
     for (int i = ; i <= n; i++) {
         pt.append(str[i]);
         for (TrieNode* p = pt.last; p && p->len > ; p = p->slink) {
             p->g = f[i - p->slink->len - p->dif];

             if (p->fail->dif == p->dif)
                 p->g = (p->g + p->fail->g) % M;
             if (!(i & ))
                 f[i] = (f[i] + p->g) % M;
         }
     }
     printf("%d", f[n]);
 }

 int main() {
     init();
     solve();
     return ;
 }