时间复杂度O(n^2)和O(nlog n)差距有多大？

0. 时间复杂度

接触到算法的小伙伴们都会知道时间复杂度（Time Complexity）的概念，这里先放出（渐进）时间复杂度的定义：

假设问题规模是\(n\)，算法中基本操作重复执行的次数是\(n\)的某个函数，用\(T(n)\)表示，若有某个辅助函数\(f(n)\)，使得

\[\lim_{n\rightarrow \infty}{T(n)/f(n)} = c
\]

其中\(c\)为不等于零的常数，则称\(f(n)\)是\(T(n)\)的同数量级函数。记作\(T(n)=O(f(n))\)，称\(O(f(n))\) 为算法的渐进时间复杂度，简称时间复杂度。

常见的时间复杂度有(表格越靠后表示越不理想)：

复杂度	名称
\(O(1)\)	常数阶
\(O(\log n)\)	对数阶
\(O(n)\)	线性阶
\(O(n\log n)\)	线性对数阶
\(O(n^2)\)	平方阶
\(O(n^3)\)	立方阶
\(O(n^k)\)	\(k\)次方阶（\(k>3\)且\(k\in Z\)）
\(O(2^n)\)	指数阶

例如，我们熟悉的插入排序（Insertion Sort）算法的时间复杂度是\(O(n^2)\)，而合并排序（Merge Sort）算法的时间复杂度是\(O(n\log n)\)

那么这些复杂度之间的差距是怎么样的呢？有些小伙伴会疑问，自己写的算法虽然是高复杂度但是也用的好好的，为什么要纠结于这个概念呢？

我们不妨来探索一下今天的问题:\(O(n^2)\)和\(O(n\log n)\)差距有多大？

1. \(O(n^2)\)和\(O(n\log n)\)差距有多大？

我们知道，插入排序（Insertion Sort）算法的时间复杂度是\(O(n^2)\)，而合并排序（Merge Sort）算法的时间复杂度是\(O(n\log n)\)，即当排序\(n\)个对象时，插入排序算法需要用时大约\(c_1n^2\)，而合并排序算法需要用时大约\(c_2n\log{n}\)，其中\(c_1\)和\(c_2\)都是正常数且与\(n\)无关，且往往\(c_1<c_2\)。

稍微利用初等数学的知识，可以知道，对于任何\(n>=2\)，比较约\(c_1n^2\)和\(c_2n\log{n}\)即比较\(c_1n\)和\(c_2\log{n}\)。由于我们已知

\[c_1<c_2
\]

以及

\[\log{n} < n
\]

想要比较这两个值的大小，直观的看法就是比较两个不等式谁的差别“更多”。可以证明，当无论\(c_1\)和\(c_2\)差别多么显著，总存在充分大的\(N\)使得当\(n>N\)时，\(c_1n>c_2\log{n}\)。

在Introduction to Algorithms中，作者举了一个很有趣的例子：

假设针对同一排序问题，用一台很快的电脑A运行插入排序，用一台很慢的电脑B运行合并排序，问题规模\(n=10^7\)：

两台电脑的差别如下，为了使A比B优势显著，作者假设电脑A性能比B强1000倍，并且B运行的代码更低效、且编译器更差（导致需要运行更多的指令）：

	电脑A	电脑B
每秒运行指令数	\(10^{10}\)	\(10^7\)
需要运行的指令总数	\(2n^2\)	\(50n\log n\)

这样,A完成任务需要：

\[\frac{2\cdot(10^7)^2}{10^{10}} = 20,000\quad seconds
\]

而B完成任务需要：

\[\frac{50\cdot 10^7\log 10^7}{10^{7}} \approx 1,163 \quad seconds
\]

可以看到，在这样的大规模的问题下，即便B计算机与A差距巨大，最终也只用了20分钟左右就完成排序，而A却需要5.5小时来完成。时间复杂度的差距可见一斑。

3. 总结

算法时间复杂度的量级差异，也许在小规模的问题下，表现差别不大。但是时间复杂度高的算法，对问题规模的变化更加敏感，因而当问题的规模变得很大的时候，靠拥有高阶时间复杂度的算法来求解并不可靠！

(更新)我从网络上找到了一个直观的各个阶的复杂度的对比，大家不妨参考一下：

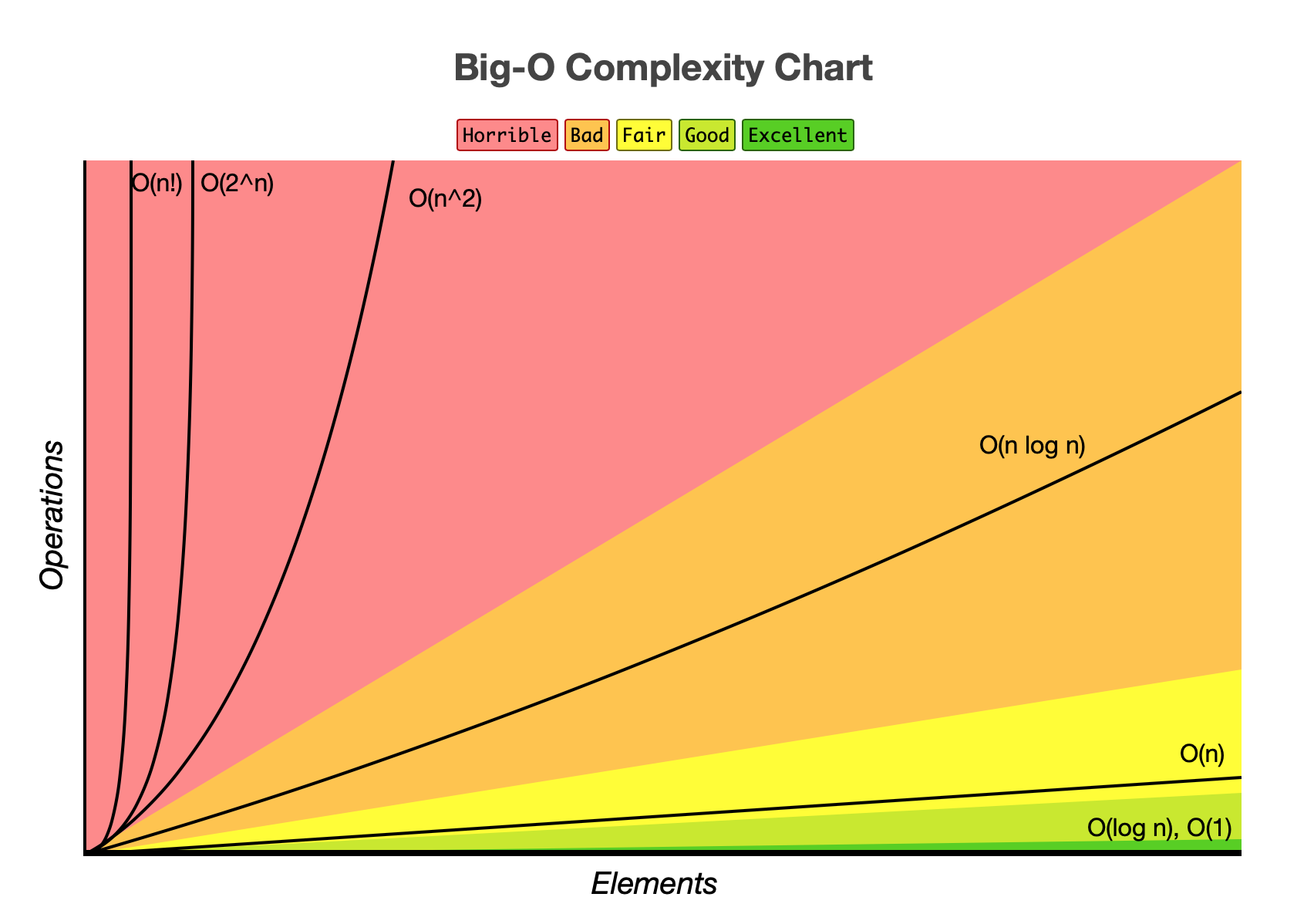
# 喜欢就点个赞、关注支持一下吧！

参考：

Thomas H. Cormen, et al., Introduction to Algorithms Part I 1.2

http://www.bigocheatsheet.com