SPFA算法

SPFA算法

一.算法简介

SPFA(Shortest Path Faster Algorithm)算法是求单源最短路径的一种算法，它是Bellman-ford的队列优化，它是一种十分高效的最短路算法。

很多时候，给定的图存在负权边，这时类似Dijkstra等算法便没有了用武之地，而Bellman-Ford算法的复杂度又过高，SPFA算法便派上用场了。SPFA的复杂度大约是O(kE),k是每个点的平均进队次数(一般的，k是一个常数，在稀疏图中小于2)。

但是，SPFA算法稳定性较差，在稠密图中SPFA算法时间复杂度会退化。

实现方法：建立一个队列，初始时队列里只有起始点，在建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。然后执行松弛操作，用队列里有的点去刷新起始点到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。

此外，SPFA算法还可以判断图中是否有负权环，即一个点入队次数超过N。

二.算法图解

给定一个有向图，求A~E的最短路。

源点A首先入队，并且AB松弛

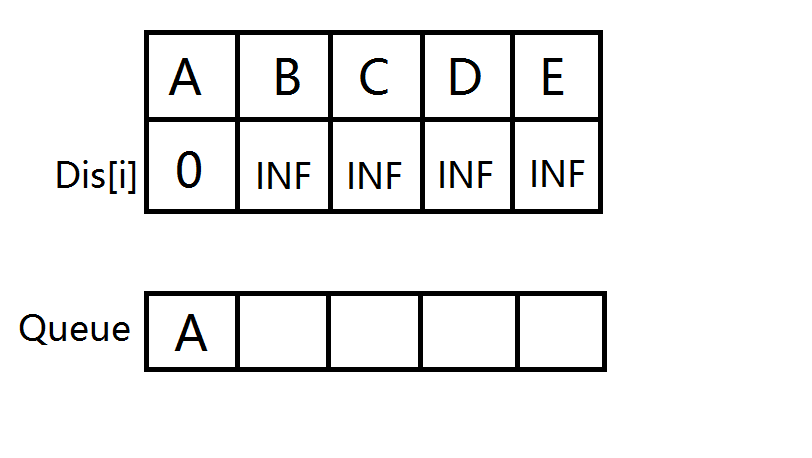
扩展与A相连的边，B，C 入队并松弛。

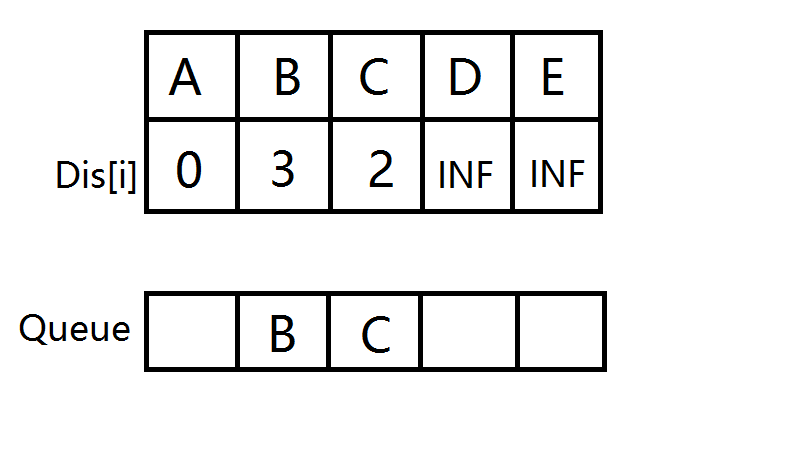
B，C分别开始扩展，D入队并松弛

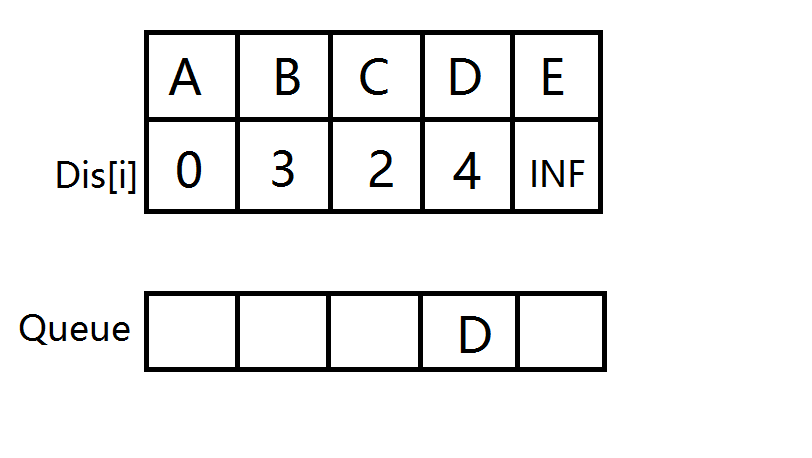
D出队，E入队并松弛。

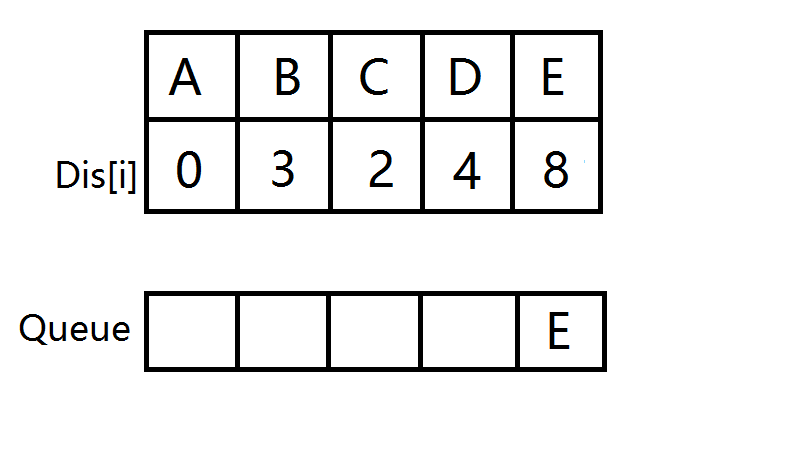
E出队，此时队列为空，源点到所有点的最短路已被找到，A->E的最短路即为8

以上就是SPFA算法的过程。

三.算法模板

 #include "bits/stdc++.h"

 using namespace std;
 const int maxN =  ;
 struct Edge
 {
     int    to , next , w ;
 } e[ maxN ];

 int    n,m,cnt,p[ maxN ],Dis[ maxN ];
 int    In[maxN ];
 bool    visited[ maxN ];

 void    Add_Edge ( const int x , const int y , const int z )
 {
     e[ ++cnt ] . to = y ;
     e[ cnt ] . next = p[ x ];
     e[ cnt ] . w = z ;
     p[ x ] = cnt ;
     return ;
 }

 bool    Spfa(const int S)
 {
     int    i,t,temp;
     queue<int>    Q;
     memset ( visited , 0 , sizeof ( visited ) ) ;
     memset ( Dis , 0x3f , sizeof ( Dis ) ) ;
     memset ( In , 0 , sizeof ( In ) ) ;

     Q.push ( S ) ;
     visited [ S ] = true ;
     Dis [ S ] = 0 ;

     while( !Q.empty ( ) )
     {
         t = Q.front ( ) ;Q.pop ( ) ;visited [ t ] = false ;
         for( i=p[t] ; i ; i = e[ i ].next )
         {
             temp = e[ i ].to ;
             if( Dis[ temp ] > Dis[ t ] + e[ i ].w )
             {
                 Dis[ temp ] =Dis[ t ] + e[ i ].w ;
                 if( !visited[ temp ] )
                 {
                     Q.push(temp);
                     visited[temp]=true;
                     if(++In[temp]>n)return false;
                 }
             }
         }
     }
     return true;
 }

 int main ( )
 {
     int    S , T ;

     scanf ( "%d%d%d%d" , &n , &m , &S , &T ) ;
     for(int i= ; i<=m ; ++i )
     {
         int x , y , _ ;
         scanf ( "%d%d%d" , &x , &y , &_ ) ;
         Add_Edge ( x , y , _  ) ;
     }

     if ( !Spfa ( S ) ) printf ( "FAIL!\n" ) ;
     else               printf ( "%d\n" , Dis[ T ] ) ;

     return ;
 }

(完)