排列 && 组合

最近编程经常遇到需要 排列&&组合（求子集） 的问题：遂整理一下。

1. 数字的排列与组合（递归）：O(n!)，O(nC(n，k)) * O(n)

#include <stdio.h>
int arr[100];
void init(int N)
{
    for(int i = 0; i < N; ++i)
        arr[i] = i+1;
}
void print(int a[], int n)
{
    for(int i = 0; i < n; ++i)
        printf("%d ", a[i]);
    printf("\n");
}

void permutation(int arr[], int begin, int end)
{
    if(begin == end) { print(arr, end); return; }
    for(int start = begin; start < end; ++start)
    {
        int t = arr[begin];
        arr[begin] = arr[start];
        arr[start] = t;
        permutation(arr, begin+1, end);
        arr[start] = arr[begin];
        arr[begin] = t;
    }
}
void combination(int endNum, int curNum, int begin, int end, int a[])
{
    if(curNum == endNum) { print(a, endNum); return; }
    for(int i = begin; i <= end; ++i)
    {
        a[curNum] = i;
        combination(endNum, curNum+1, i+1, end, a);
    }
}
int main()
{
    int N;
    scanf("%d", &N);

    printf("Combination: \n");
    int a[30] = {0};
    for(int numberOfElem = 1; numberOfElem <= N; ++numberOfElem)
        combination(numberOfElem, 0, 1, N, a);

    init(N);
    printf("Permutation:\n");

    permutation(arr, 0, N);
    return 0;
}

2. 字符的排列组合

#include <stdio.h>
#include <string.h>
char s[] = "ABC";

void print(const char a[], int n)
{
    for(int i = 0; i < n; ++i)
        printf("%c ", a[i]);
    printf("\n");
}

void permutation(char s[], int begin, int end)
{
    if(begin == end) { print(s, end); return; }
    for(int start = begin; start < end; ++start)
    {
        char t = s[begin];
        s[begin] = s[start];
        s[start] = t;
        permutation(s, begin+1, end);
        s[start] = s[begin];
        s[begin] = t;
    }
}
void combination(int endNum, int curNum, int begin, int end, char a[], const char s[])
{
    if(curNum == endNum) { print(a, endNum); return; }
    for(char i = begin; i < end; ++i)
    {
        a[curNum] = s[i];
        combination(endNum, curNum+1, i+1, end, a, s);
    }
}
int main()
{
    int N = strlen(s);

    printf("Combination: \n");
    char a[30] = {0};
    for(int members = 1; members <= N; ++members)
        combination(members, 0, 0, N, a, s);

    printf("Permutation:\n");
    permutation(s, 0, N);
    return 0;
}

3.数字的组合（非递归）Θ(n2ⁿ) * O(n)：

#include <stdio.h>
unsigned long long count = 1;

int main()
{
    int n, k, i, j, c;
    scanf("%d", &n);
    for(k = 1; k <= n; ++k)
    {
        for (i=0; i<(1<<n); i++)
        {
            for (j=0,c=0; j<32; j++) if (i & (1<<j)) c++;
            if (c == k)
            {
                for (j=0;j<32; j++) if (i & (1<<j)) printf ("%i ", j+1);
                printf ("\n");
                ++count;
            }
        }
    }
    printf("total: %d\n", count);
}

另外：http://www.cnblogs.com/autosar/archive/2012/04/08/2437799.html 写的不错，可以学习一下。

8月29号。

忽然想起来小时候经常玩的快算 24.

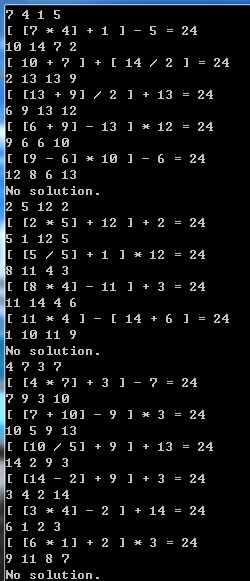
试着利用全排列算法，写了个快算24的小程序。效果还不错。

思想：1、4个数字全排列，对每一个排列，从头到尾计算一遍。共 4！* 4³次计算 。 2、 取出所有的两两组合，2 * C(4,2) 种方案, 共 2 * C(4,2) * 4³次计算；但是利用全排列，对于每一个排列，取前两个和后两个组合整好是 2 * C(4,2) = 4！种方案。 故总计算复杂度为： 4! * 4³ = 42 * 64 =  2688 次（* 2）。

#include <iostream>
using namespace std;
const int v = 24;
int A[4];
const char ch[4] = { '+', '-', '*', '/'};
bool has_answer = false;
int compute(const char ch, int v1, int v2) {
	switch(ch) {
	case '+': return v1+v2;
	case '-': return v1 > v2 ? v1-v2 : -10000;
	case '*': return v1*v2;
	default:
		{
			if(v2 == 0) return -10000;
			float tem = (float)(v1)/v2;
			int tem2 = v1 / v2;
			if(abs(tem-tem2) > 0) return -10000;
			return tem2;
		};
	}
}
bool compute24() {
	int l, m, n;
		for(l = 0; l < 4; ++l) {
			int v2 = compute(ch[l], A[0], A[1]);
			for(m = 0; m < 4; ++m) {
				int v3 = compute(ch[m], v2, A[2]);
				for(n = 0; n < 4; ++n) {
					if(has_answer) return true;
					if(compute(ch[n], v3, A[3]) == v) {
						cout << "[ [" << A[0] << ' ' << ch[l] << ' ' << A[1] << "] " << ch[m] << ' '
							<< A[2] << " ] " << ch[n] << ' ' << A[3] << " = " << v << endl;
						return has_answer = true;
					}
					else if(compute(ch[m], v2, compute(ch[n], A[2], A[3])) == v) {
						cout << "[ " << A[0] << ' ' << ch[l] << ' ' << A[1] << " ] " << ch[m] << " [ "
							<< A[2] << ' ' << ch[n] << ' ' << A[3] << " ] = " << v << endl;
						return has_answer = true;
					}

				}
			}
		}
	return has_answer;
}

void permutation(int begin) {
	if(begin == 4) {
		compute24();
		return;
	}
	for(int start = begin; start < 4; ++ start) {
		int tem = A[start];
		A[start] = A[begin];
		A[begin] = tem;
		permutation(begin+1);
		A[begin] = A[start];
		A[start] = tem;
	}
}

int main() {
	while(true) {
		has_answer = false;
		for(int k = 0; k < 4; ++k) {
			cin >> A[k];
		}
		permutation(0);
		if(!has_answer) cout << "No solution." << endl;
	}
	system("pause");
	return 0;
}

准备的测试用例： {9, 10, 5, 2}, {5, 6, 7, 9}, {5, 5, 5, 5}, {7, 11, 9, 13}, {3, 7, 11, 3}, {9, 5, 6, 2}, {5, 6, 9, 11}, {10, 11, 2, 2}

使用随机数生成：

/* modify the function main(), as follows: */
int main() {
	while(true) {
		has_answer = false;
		srand((unsigned)time(NULL));
		for(int k = 0; k < 4; ++k) {
			A[k] = rand() % 14 + 1;
			cout << A[k] << ' ';
		}
		cout << endl; Sleep(10000);
		permutation(0);
		if(!has_answer) cout << "No solution." << endl;
		Sleep(10000);
	}
	system("pause");
	return 0;
}