P5179 Fraction 题解

题目描述

给你四个正整数 $a,\,b,\,c,\,d$ ，求一个最简分数 $\frac{p}{q}$ 满足 $\frac{a}{b} < \frac{p}{q} < \frac{c}{d}$。

若有多组解，输出 $q$ 最小的一组，若仍有多组解，输出 $p$ 最小的一组。

前置知识：Stern-Brocot 树

首先引入分数逼近。这里的分数逼近是指用用一个分数来逼近另一个分数，使得误差趋于零。例如，假设需要逼近的分数为 $\dfrac{r}{s}$，有分数 $\dfrac{u}{v} > \dfrac{r}{s}$。那么有以下结论：

\[\dfrac{r}{s} \leq \dfrac{r + u}{s + v} \leq \dfrac{u}{v}
\]

具体等号能不能取到记不清了，不过不影响。结论很好证明，下面证一下。

将 $\dfrac{r + u}{s + v}$ 与 $\dfrac{r}{s}$ 做减法，得到 $\dfrac{r + u}{s + v} - \dfrac{r}{s} = \dfrac{(r + u)s - r(s + v)}{s(s + v)} = \dfrac{us- vr}{s(s + v)}$。

因为 $\dfrac{r}{s} < \dfrac{u}{v}$，两边同时乘以 $sv$，得 $vr < us$，即 $us - vr > 0$。

又因为 $s(s + v) > 0$，所以 $\dfrac{us - vr}{s(s + v)} > 0$。证毕。

注意上面结论和证明成立的条件是 $u, v, s, r > 0$。

接下来引入 Stern-Brocot 树这个概念。

Stern-Brocot 树可以维护所有的正分数。这一点可以被我们用来解决这道题目。

首先介绍一下 Stern-Brocot 树。这个树由 $\dfrac{0}{1}$ 和 $\dfrac{1}{0}$ 两个分数开始。$\dfrac{1}{0}$ 不大好定义，暂且把它当做 $+ \infty$。将这两个分数作为源节点。

接下来，像我们刚才讨论的分数逼近，将 $\dfrac{0}{1}$ 和 $\dfrac{1}{0}$ 的分子分母分别相加，得到另外一个分数 $\dfrac{1}{1}$。这个分数确实在 $\dfrac{0}{1}$ 与 $\dfrac{1}{0}$ 之间。$\dfrac{1}{1}$ 被成为第 $1$ 层迭代后的节点。

同样的，将 $\dfrac{1}{1}$ 与 $\dfrac{0}{1}, \dfrac{1}{0}$ 分别进行操作，得到两个分数，称为第二次迭代。

所以我们得到了 Stern-Brocot 树的构建基础：将 $\dfrac{a}{b}$ 与 $\dfrac{c}{d}$ 分子分母分别相加，得到 $\dfrac{a + c}{b + d}$ 作为下一轮迭代的节点。

例如，进行三次操作后，这棵树就会变成这样：

\[\begin{array}{c} \dfrac{0}{1}, \dfrac{1}{1}, \dfrac{1}{0} \\\\ \dfrac{0}{1}, \dfrac{1}{2}, \dfrac{1}{1}, \dfrac{2}{1}, \dfrac{1}{0} \\\\ \dfrac{0}{1}, \dfrac{1}{3}, \dfrac{1}{2}, \dfrac{2}{3}, \dfrac{1}{1}, \dfrac{3}{2}, \dfrac{2}{1}, \dfrac{3}{1}, \dfrac{1}{0} \end{array}
\]

注意，某些节点（就是第 $i$ 层存在，第 $i + 1$ 层也存在的节点），实际上在第 $i + 1$ 层是不会出现的。只是为了方便比较加了上去。

可以看到，第三层的第二个分数 $\dfrac{1}{3}$ 就是左右两边两个数分子分母分别相加的和。第四个，第六个和第八个以此类推。

下面是来自 OI-wiki 的一张图。

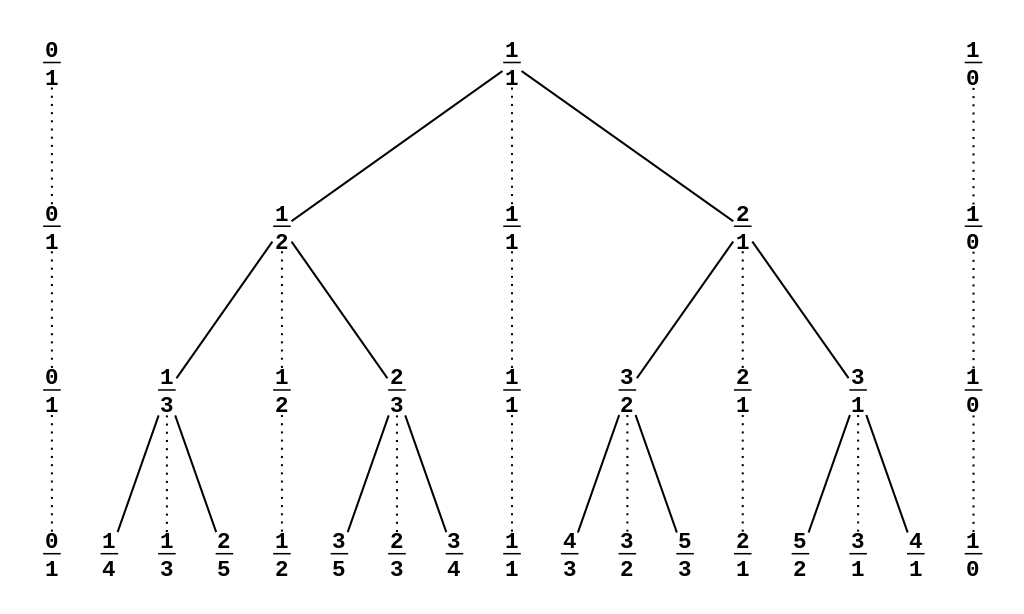
刚才所提到的不存在的节点就是虚线相连的那些节点。可以看到，这棵树具有二叉结构。因此在这棵树上搜索只需要花费 $O(\log_2 n)$ 的时间。非常优秀。

关于最简性的证明可以看 OI-wiki 上的解释。这里不再赘述。

对于这道题，显然可以在 Stern-Brocot 树上二分来求解。具体的，如果当前结果 $\dfrac{x}{y}$ 在左端点 $\dfrac{A}{B}$ 的左边，则向右递归，反之亦然。于是可以写出这样的代码：

void solve(int a = 0, int b = 1, int c = 1, int d = 0) {

	int x = a + c, y = b + d;

	long double now = (long double)x / y;

	long double L = (long double)A / B, R = (long double)C / D;

	if (now > L && now < R) {

		ans = {x, y}; return;

	}

	if (now <= L) solve(x, y, c, d);

	else solve(a, b, x, y);

}

交上去以后发现只有 $60$ 分。说明我们需要继续优化算法。

如果把递归时的路径打印出来，我们发现可能会连续地向左（向右）递归很多次。这很不好，因为浪费了许多时间。那么是否可以用较短的复杂度计算出接下来需要连续向左（向右）递归多少次呢？

答案是可以的。假设当前的递归函数是 $(a, b, c, d)$，当前分数 $\dfrac{x}{y} = \dfrac{a + c}{b + d}$。假设 $\dfrac{A}{B} < \dfrac{x}{y} < \dfrac{C}{D}$，这是最好的，可以直接输出了。但是如果 $\dfrac{x}{y} \le \dfrac{A}{B}$，显然需要向右递归。假设向右递归的次数为 $t$，那么 $\dfrac{x + ct}{y + dt} \ge \dfrac{A}{B}$。解一下这个不等式：

\[\begin{array}{c} \dfrac{x + ct}{y + dt} \ge \dfrac{A}{B} \\\\ (x + ct)B \ge (y + dt)A \\\\ xB + cBt \ge yA + dAt \\\\ t \ge \dfrac{yA - xB}{cB - dA} \end{array}
\]

同理，如果 $\dfrac{x}{y} \ge \dfrac{C}{D}$，那么需要连续向左递归的次数 $t \ge \dfrac{yC - xD}{aD - bC}$。

如此，我们用 $O(1)$ 的时间求出了连续向左（向右）递归的次数。

代码

#include <algorithm>

#include <cstdio>

#include <iostream>

using namespace std;

using PII = pair<int, int>;

PII ans;

int A, B, C, D;

void solve(int a = 0, int b = 1, int c = 1, int d = 0) {

    int x = a + c, y = b + d;

    long double now = (long double)x / y;

    long double L = (long double)A / B, R = (long double)C / D;

    if (now > L && now < R) {

        ans = {x, y}; return;

    }

    if (now <= L) {

        int t = (int)(y * A - x * B) / (c * B - d * A);

        solve(x + c * t, y + d * t, c, d);

    }

    else {

        int t = (int)(y * C - x * D) / (a * D - b * C);

        solve(a, b, x + a * t, y + b * t);

    }

}

signed main() {

    while (scanf("%d%d%d%d", &A, &B, &C, &D) != EOF) {

        solve();

        printf("%d/%d\n", ans.first, ans.second);

    }

    return 0;

}

简短精炼得代码后面有个小坑：别忘了用 long double。

最后留个 Stern-Brocot 树的练习题：P1298 最接近的分数。