洛谷3830 [SHOI2012]随机树 【概率dp】

题目

输入格式

输入仅有一行，包含两个正整数 q, n，分别表示问题编号以及叶结点的个数。

输出格式

输出仅有一行，包含一个实数 d，四舍五入精确到小数点后 6 位。如果 q = 1，则 d 表示叶结点平均深度的数学期望值；如果 q = 2，则 d 表示树深度的数学期望值。

输入样例

1 4

输出样例

2.166667

提示

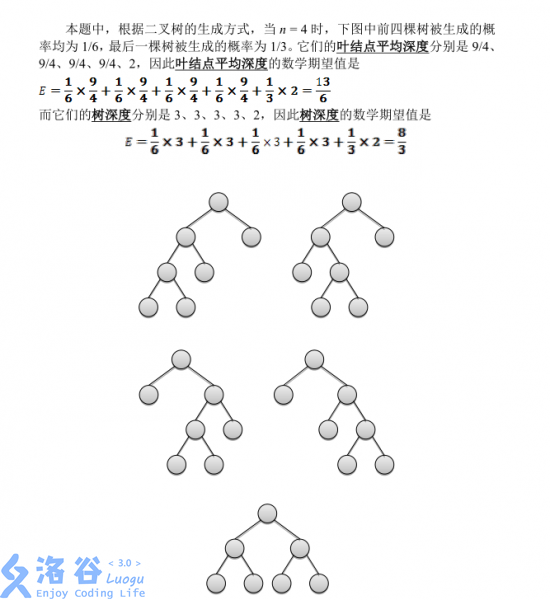
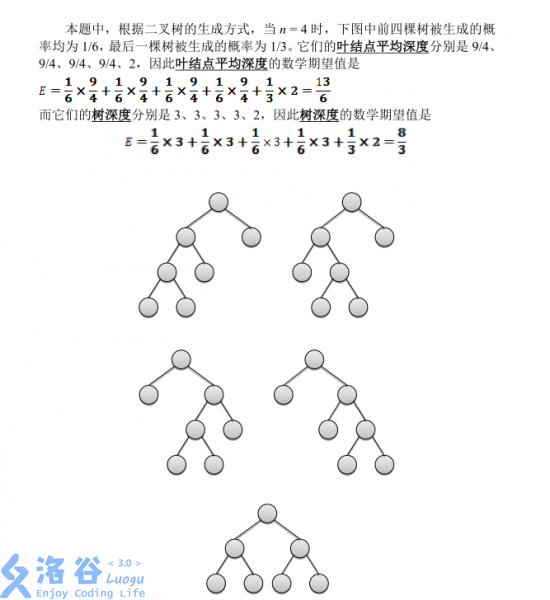
题解

第一问比较简单，我们设\(f[i]\)表示第\(i\)次扩展的期望深度

那么

\[f[i] = \frac{f[i - 1] * (i - 2) + (f[i - 1] + 1) * 2}{i}
\]

化简得

\[f[i] = f[i - 1] + \frac{2}{i}
\]

第二问

首先我们有这样一个整数概率公式：

\[E(x) = \sum_{i = 1}^{+\infty} P(x >= i)
\]

含义为：随机变量\(x\)的期望为所有\(x>=i\)的概率之和

那我们设\(f[i][d]\)表示有\(i\)个叶子，深度\(>=d\)的概率，

那么

\[ans = \sum_{i = 1}^{n - 1} f[n][i]
\]

考虑转移，我们枚举左右子树分到多少叶子

\[f[i][d] = \sum_{j = 1}^{i - 1} \frac{f[j][d - 1] + f[i - j][d - 1] - f[j][d - 1]*f[i - j][d - 1]}{i - 1}
\]

其实就是一个容斥，两边都大于\(d - 1\)的部分会被算两次，减去一次即可

这样我们就做完了

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");
using namespace std;
const int maxn = 205,maxm = 100005,INF = 1000000000;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
double f[maxn][maxn];
int n,t,m;
void solve1(){
	double ans = 0;
	for (int i = 2; i <= n; i++){
		ans += 2.0 / i;
	}
	printf("%.6lf\n",ans);
}
void solve2(){
	for (int i = 1; i <= n; i++) f[i][0] = 1;
	for (int i = 2; i <= n; i++){
		for (int d = 1; d < i; d++){
			for (int j = 1; j < i; j++)
				f[i][d] += (f[j][d - 1] + f[i - j][d - 1] - f[j][d - 1] * f[i - j][d - 1]) / (i - 1);
		}
	}
	double ans = 0;
	for (int i = 1; i < n; i++) ans += f[n][i];
	printf("%.6lf\n",ans);
}
int main(){
	t = read(); n = read();
	if (t & 1) solve1();
	else solve2();
	return 0;
}