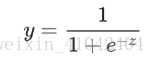学习笔记（七）： Logistic Regression

目录

Calculating a Probability

Model Training

1.Loss function for Logistic Regression

2.Regularization in Logistic Regression

Glossay

---

Calculating a Probability

Many problems require a probability estimate as output. Logistic regression is an extremely efficient mechanism for calculating probabilities. Practically speaking, you can use the returned probability in either of the following two ways:

• "As is"

• Converted to a binary category.

Let's consider how we might use the probability "as is." Suppose we create a logistic regression model to predict the probability that a dog will bark during the middle of the night. We'll call that probability:

p(bark | night)

If the logistic regression model predicts a p(bark | night) of 0.05, then over a year, the dog's owners should be startled awake approximately 18 times:

startled = p(bark | night) * nights

18 ~= 0.05 * 365

In many cases, you'll map the logistic regression output into the solution to a binary classification problem, in which the goal is to correctly predict one of two possible labels (e.g., "spam" or "not spam").

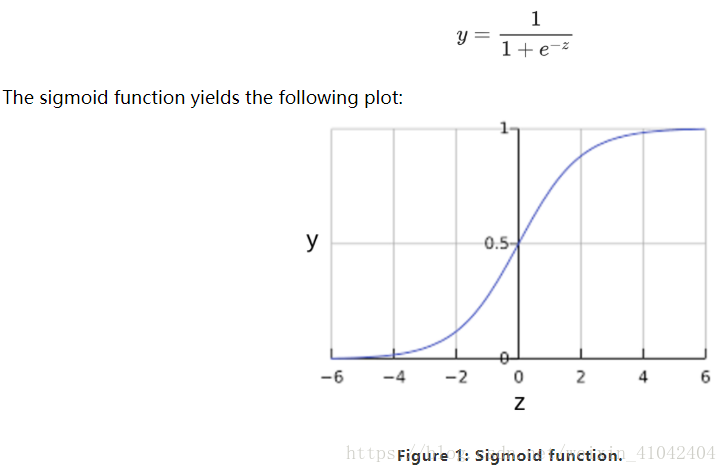
You might be wondering how a logistic regression model can ensure output that always falls between 0 and 1. As it happens, a sigmoid function, produces output having those same characteristics:

If z represents the output of the linear layer of a model trained with logistic regression, then sigmoid(z) will yield a value (a probability) between 0 and 1. 如果 z 表示使用逻辑回归训练的模型的线性层的输出，则 S 型(z) 函数会生成一个介于 0 和 1 之间的值（概率）。

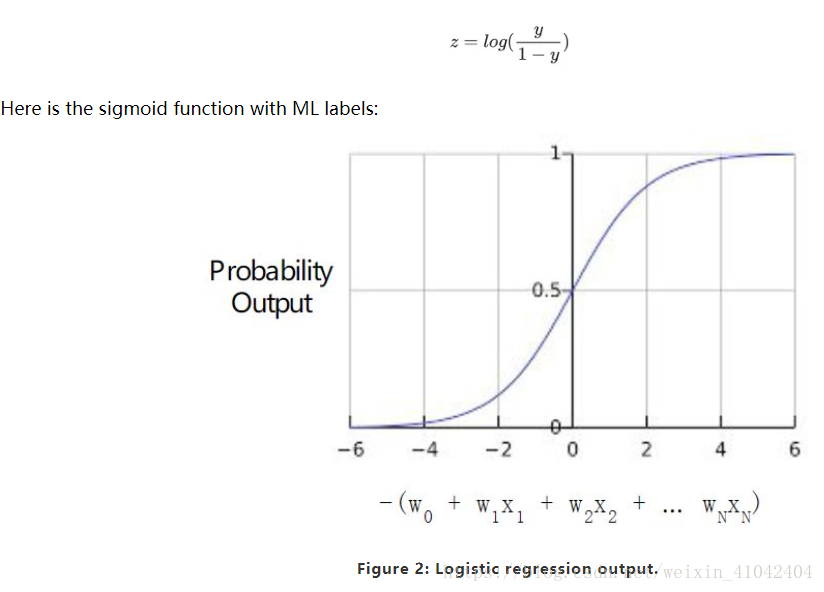
Note that z is also referred to as the log-odds 对数几率 because the inverse of the sigmoid S函数的反函数 states that z can be defined as the log of the probability of the "1" label (e.g., "dog barks") divided by the probability of the "0" label (e.g., "dog doesn't bark"):

Sample logistic regression inference calculation

---

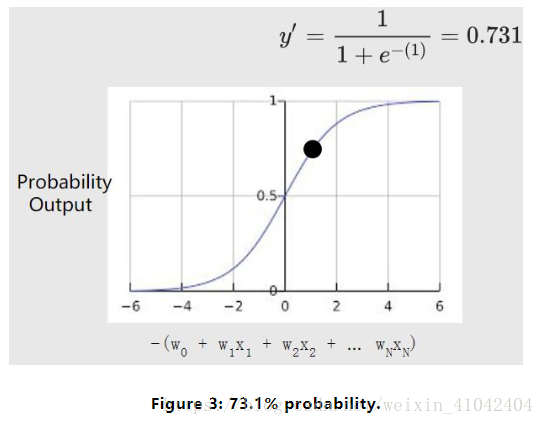
Suppose we had a logistic regression model with three features that learned the following bias and weights:

b = 1,w1 = 2,w2 = -1,w3 = 5

Further suppose the following feature values for a given example:

x1 = 0,x2 = 10,x3 = 2

Therefore, the log-odds:

b+w1x1+w2x2+w3x3

will be:

(1) + (2)(0) + (-1)(10) + (5)(2) = 1

Consequently, the logistic regression prediction for this particular example will be 0.731:

 Model Training

1.Loss function for Logistic Regression

---

The loss function for linear regression is squared loss.

The loss function for logistic regression is Log Loss, which is defined as follows:

The equation for Log Loss is closely related to Shannon's Entropy measure from Information Theory.

对数损失函数的方程式与”Shannon 信息论中的熵测量“密切相关。

It is also the negative logarithm of the likelihood function, assuming a Bernoulli distribution of y.

它也是似然函数的负对数（假设“y”属于伯努利分布）。

Indeed, minimizing the loss function yields a maximum likelihood estimate.

最大限度地降低损失函数的值会生成最大的似然估计值。

2.Regularization in Logistic Regression

---

Regularization is extremely important in logistic regression modeling. Without regularization, the asymptotic nature渐进性 of logistic regression would keep driving loss towards 0 in high dimensions. Consequently, most logistic regression models use one of the following two strategies to dampen model complexity:

• L2 regularization.

• Early stopping, that is, limiting the number of training steps or the learning rate.

• L1 regularization.

Imagine that you assign a unique id to each example, and map each id to its own feature. If you don't specify a regularization function, the model will become completely overfit. That's because the model would try to drive loss to zero on all examples and never get there, driving the weights for each indicator feature to +infinity or -infinity.

This can happen in high dimensional data with feature crosses, when there’s a huge mass of rare crosses that happen only on one example each.当有大量罕见的特征组合且每个样本中仅一个时，包含特征组合的高维度数据会出现这种情况。

Fortunately, using L2 or early stopping will prevent this problem.

Summary

• Logistic regression models generate probabilities.

• Log Loss is the loss function for logistic regression.

• Logistic regression is widely used by many practitioners.

Glossay 

1.sigmoid function:

A function that maps logistic or multinomial regression output (log odds) to probabilities, returning a value between 0 and 1:

where z in logistic regression problems is simply:

z=b+w1x1+w2x2+…wnxn

In other words, the sigmoid function converts z into a probability between 0 and 1.

In some neural networks, the sigmoid function acts as the activation function.

2.binary classification:

A type of classification task that outputs one of two mutually exclusive互斥 classes.

For example, a machine learning model that evaluates email messages and outputs either "spam" or "not spam" is a binary classifier.

3.logistic regression:

A model that generates a probability for each possible discrete label value in classification problems by applying a sigmoid function to a linear prediction.

Although logistic regression is often used in binary classification problems, it can also be used in multi-class classification problems (where it becomes called multi-class logistic regression or multinomial多项 regression).

4.Log Loss:

The loss function used in binary logistic regression二元逻辑回归.

5.log-odds对数几率:

The logarithm of the odds of some event.

If the event refers to a binary probability, then odds refers to the ratio of the probability of success (p) to the probability of failure (1-p).

For example, suppose that a given event has a 90% probability of success and a 10% probability of failure. In this case, odds is calculated as follows:

odds=p/(1-p)=.9/.1=9

The log-odds is simply the logarithm of the odds.

By convention, "logarithm" refers to natural logarithm, but logarithm could actually be any base greater than 1. 按照惯例，“对数”是指自然对数，但对数实际上可以是大于1的任何基数。

Sticking to convention, the log-odds of our example is therefore:

log-odds=ln(9) =2.2

The log-odds are the inverse of the sigmoid function.