AtCoder Beginner Contest 137

前言

又是卡在了T4 ， 总分 100 + 200 + 300 = 600pts rank 2449。以后还是要多积累比赛经验。

A

输出a+b，a-b，a*b中最大的数，还要多简单？不挂代码了

Ｂ

题目描述

• 数字线上有2000001块石头。这些石头的坐标是- 1000000，- 999999 ，- 999998 ，... ，999999 ，1000000。其中，一些ķ连续的石头涂成黑色，其他石头涂成白色。另外，我们知道坐标X处的石头黑色的。打印所有可能包含黑色石头的坐标，按升序排列。

数据范围

• 1 ≤ ķ ≤ 100
• 0 ≤ X ≤ 100
• 输入中的所有值都是整数。

看不懂？（我也看不懂） 还是看样例算了（我是看样例懂的）

样例输入 3 7

样例输出 5 6 7 8 9

解释： 我们知道有三块石头漆成黑色，坐标7处的石头漆成黑色。有三种可能的情况：\(567\)，\(678\)，\(789\) ，故56789

题解

这下懂了吧？

以x为原点，向左延伸k格，向右延伸k格，输出这个区间。

Code

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<cmath>
#define N 1000000
using namespace std;
inline int read() {
	int x=0,f=1; char ch=getchar();
	while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
	return x * f;
}
int k,x;
int main()
{
	k = read() ,x = read();
	int l = max(-N , x-k+1);
	int r = min(N , x+k-1);
	for(int i=l;i<=r;++i)
		printf("%d ",i);
	return 0;
}

C

题目描述

给定\(n(2<=n<=10^5)\)个字符串，问有多少对字符串本质是一样的（即组成的字母一样）？

如 killbunny 和 bunnykill本质是一样的，所以他们构成一对本质一样的字符串（题目保证全是小写且字符串长度均为10）。

题解

想到了把每种本质相同的字符串变成一样的

或者直接说每个字符串排一下序，如 bbbcccaaad 变成 aaabbbcccd （按字典序），就解决本质相同的字符串了

用map来处理本质相同字符串有多少个，然后考虑每个本质相同的字符串的贡献

举例 ： 如果本质都是 killbunny 的字符串有3个，这中间就能两两连线连出 2 + 1条线，脑补一下，不难发现，如果本质都是killbunny的字符串有4个，两两配对就能有3 + 2 + 1条线。 故有本质相同的字符串m个，就有n-1 + n-2 + ... + 2 + 1条线，也就是有多少对。根据公式可以快速算这个结果。

Code

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
#define int long long
using namespace std;
inline int read() {
	int x=0,f=1; char ch=getchar();
	while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
	return x * f;
}
const int N = 1e5+7;
map<string,int> mp;
string name[N];
int n,cnt,ans;
signed main()
{
	cin>>n;
	int len = 10;
	for(int i=1;i<=n;++i) {
		char s[15];
		cin>>s;
		sort(s,s+strlen(s));
		if(!mp[s]) name[++cnt] = s;
		mp[s]++;
	}
	for(int i=1;i<=cnt;++i) {
		int num = mp[name[i]];
		num--; ans += ( (1+num)*num ) / 2;
	}
	printf("%lld\n",ans);
	return 0;
}

D

贪心　＋　（堆？）

题目描述：

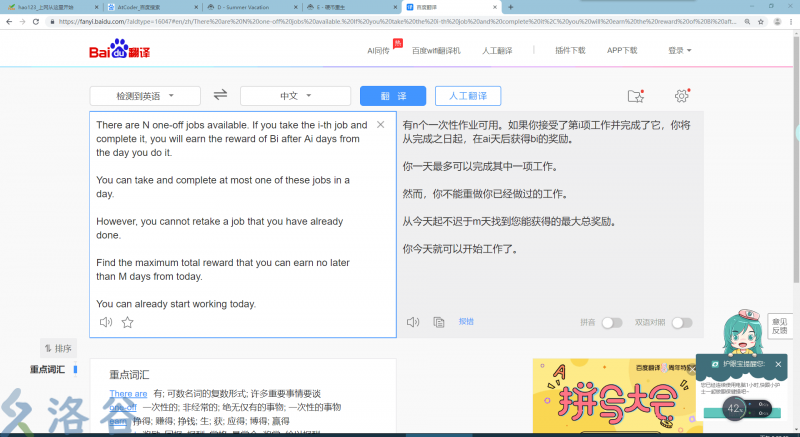
数据范围

题解

贪心策略：按时间将任务排序，把 \(i\) 时刻能做的任务都扔进堆里 ， 因为任务是一次性的，所以每个任务放进去过就不再放入了。然后每个时刻看一下堆里面有没有数，有的话就取堆顶出来，而且每个时刻只能取一次。正确性显然。

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1; char ch=getchar();
	while(ch<'0' || ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9'){ x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
	return x*f;
}
const int N=1e5+7;
int n,m,ans;
struct Node{
	int a,b;
	bool operator < (const Node &x)const {
		return a < x.a;
	}
}t[N];
priority_queue<int>q;
int main()
{
	n=read() ,m=read();
	for(int i=1;i<=n;++i) {
		t[i].a=read(),t[i].b=read();
	}
	sort(t+1,t+1+n);
	for(int i=1,j=1;i<=m;++i) {
		for(;j<=n;++j) {
			if(i<t[j].a) break;
			q.push(t[j].b);
	    }
		if(!q.empty()) {
			ans += q.top();
			q.pop();
		}
	}
	printf("%d",ans);
	return 0;
}

E

题目描述

给你一张有权有向图（权值叫做硬币），初始在1节点，有0硬币，每走一条路花费p硬币，到达n节点可以选择结束或者不结束，问可否有权值最大，有就输出，没有就输出-1。

n<=2500 m<=5000

题解

遇到这种题目可以先把每条边减去p，这样就是经过这条边可获得的权值了。

如果从某个点u到v可更新权值，那么就更新一下。

如果更新了n次还能更新就说明形成了可以无限更新的环，则置为INF

Code （如果有那位大佬理解得更透彻欢迎评论解释一下）

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<cmath>
#define N 2507
#define M 5007
#define int long long
using namespace std;
inline int read() {
	int x=0,f=1; char ch=getchar();
	while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
	return x * f;
}
const int INF = 1e18;	//longlong的INF不是0x3f3f3f
int n,m,p;
int f[N];
struct Edge {
	int u,v,d;
}E[M];
signed main()
{
	n = read() ,m = read() ,p = read();
	for(int i=1,u,v,d;i<=m;++i) {
		u = read() ,v = read() ,d = read();
		E[i] = (Edge){u,v,d-p};
	}
	for(int i=1;i<=n;++i) f[i] = -INF;
	f[1] = 0;
	for(int i=1;i<=n*2;++i) {
		for(int j=1;j<=m;++j) {
			int u = E[j].u ,v = E[j].v ,d = E[j].d;
			if(f[u]==-INF) continue;
			if(f[u]+d > f[v]) {
				f[v] = i<=n ? f[u]+d : INF;
			}
		}
	}
	if(f[n]==INF) puts("-1");
	else if(f[n]<0) puts("0");
	else printf("%lld\n",f[n]);
	return 0;
}

F

先挖坑，待会去学怎么做