FFT IP核调用与仿真之FFT数学分析

对于FFT这个IP核，我其实对它真的是又爱又恨，因为它真的耗费了我太多时间，但是随着研究的深入，遇到的问题一点点给消化解决，终于不用带着问题睡觉了，哈哈，有时候真的挺佩服自己的，遇到不懂的，不了解的，真的不允许自己留一点疑惑，必须深挖到底，一点含糊都不留给自己，其实，不知道大家有没有这样的疑惑，现在不懂的，懒得去研究的，估计过不了多久这个知识点又会兜回来找你的。我有时候也会侥幸自己能逃过不会做的任务，但是真的过不了多久，我越是不会的东西就越是会来找我，感觉今天的话有点多，赶紧回到正题上来。FFT是什么？我也曾经花了大半个月的时间去研究过它的原理，还手写代码不调用IP核去实现它的计算，这个实现过程还是挺复杂的，所以最简单易上手的还是好好学会调用IP核吧，这个IP核真的忒好用呢。

FFT其实本质上就是用来做频谱分析的，我给你一堆混杂的频谱，你知道里面有哪些频率吗？你不知道，但是FFT知道，它能帮你分析混杂频谱中有哪些频率成分。说得官方一点就是：FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域，有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了，这就是很多信号分析采用FFT变换的原因。简单来说，FFT的作用就是对信号进行频谱分析。

我们首先结合MATALB这个强大的数学分析软件来生动阐释下FFT这个概念，它可以拿来做什么？它是如何实现频谱分析的？一个模拟信号，经过ADC采样之后，就变成了数字信号，我们就可以拿采样得到的数字信号，做FFT变换。N个采样点，经过FFT之后，就可以得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。 例如某点n所表示的频率为：Fn=(n-1)*Fs/N。由这条公式可以看出，Fn所能分辨到的频率为Fs/N，举例来说如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，那这个对应的时间序列点数就是2048，则结果可以分析到0.5Hz。所以如果要提高频率分辨力，则必须增加采样点数，也即采样时间。频率分辨率和采样时间是倒数关系。由于FFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果。

  假设我们有一个信号，它含有2V的直流分量，里面包含频率为5MHz、相位为-30度、幅度为3V的交流信号，以及一个频率为7.5MHz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下：    S1=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);%它含有2V的直流分量，频率为5MHz、相位为-30度、幅度为3V的交流信号，以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号，这里式中的cos参数为弧度，所以-30度和90度要分别换算成弧度。我们以25.6MHz的采样率对这个信号进行采样，总共采样256点。根据公式：Fn=(n-1)*Fs/N，我们可以知道，每两个点之间的间距就是0.1MHz，也就是它的分辨率是0.1MHZ，第n个点的频率就是n-1。我们的信号有3个频率：0MHz、5MHz、7.5MHz，根据公式，n分别在1、51、76，也就是应该分别在第1个点、第51个点、第76个点上出现峰值，其它各点应该接近0。

实际情况如何呢？我们把S1这个交流信号灌进去MATLAB看看计算结果：

   1）峰值出现位置：我们可以看到在第1个点、第51个点、第76个点上分别出现峰值：

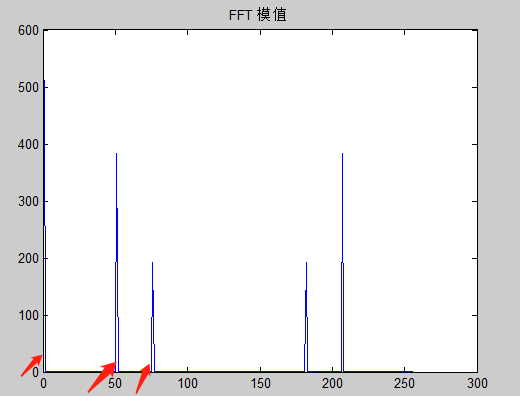
2）信号幅值对比：

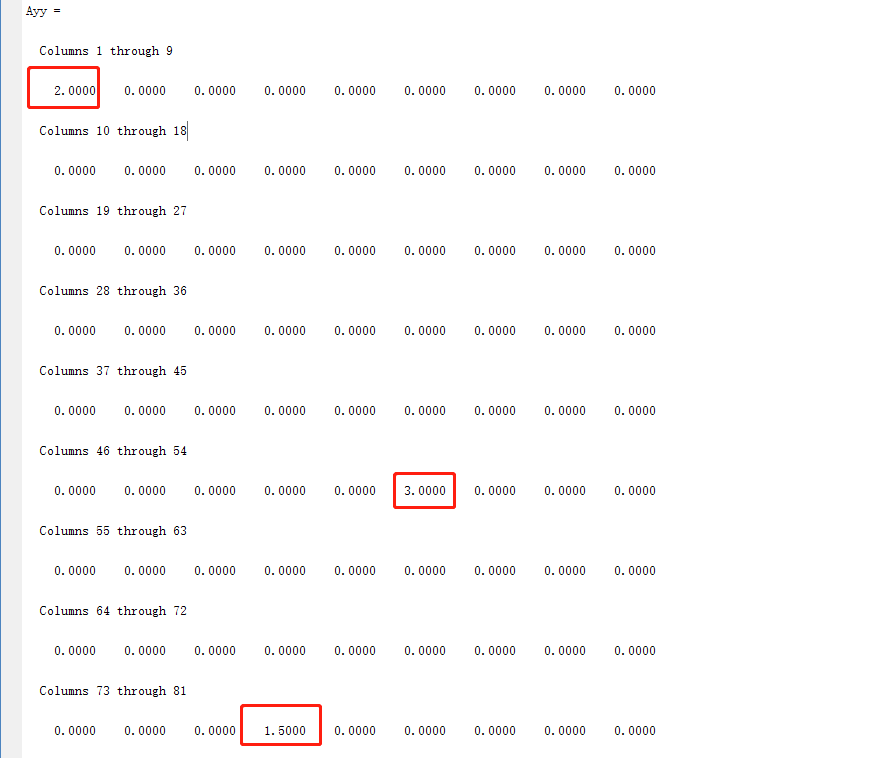
预测猜想：按照我们的原始频率输入，第1个点、第51个点、第76个点的幅度值分别是2、3、1.5；

Matlab输出结果：

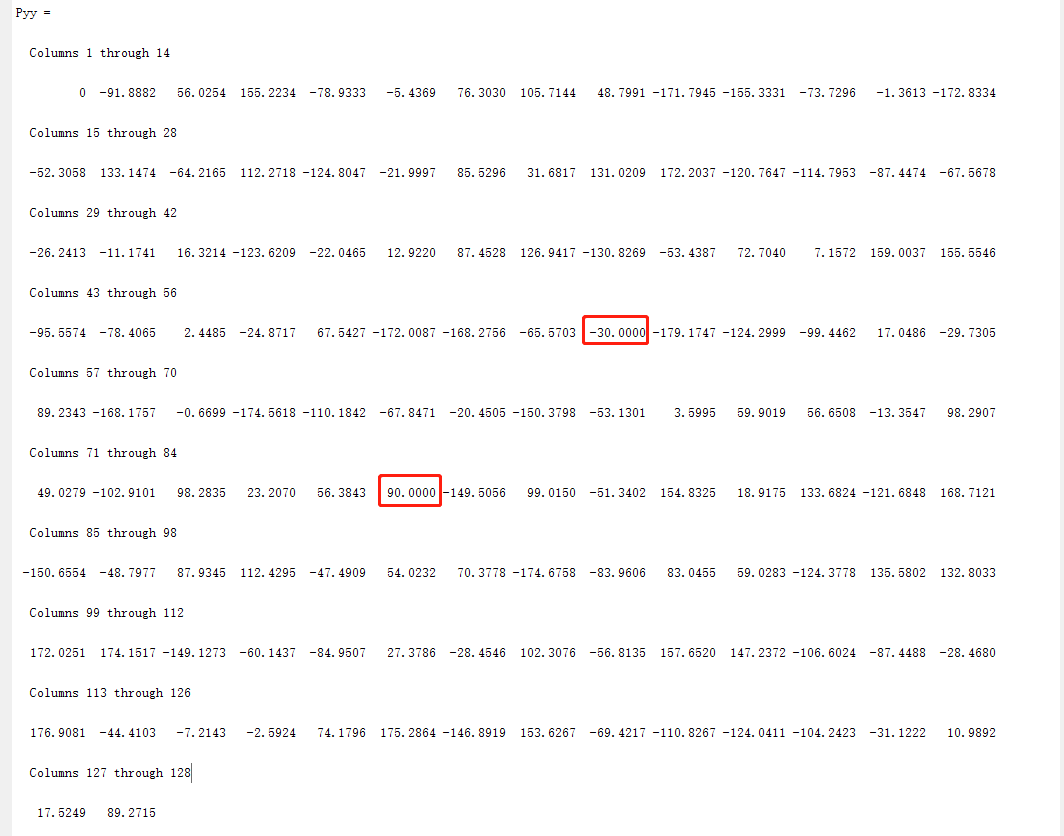
3）相位输出验证：

预测猜想：第1个点直流分量没有相位输出，不管，第51个点、第76个点的幅度值分别是-30，90；

Matlab输出结果：

   以上就是FFT结合Matlab的数学分析，这个例子是我们预先知道了频率的成分，然后利用FFT对原始信号作FFT运算，最后根据运算结果提取到的频谱来验证是否是我们灌进来的那些频率信号。在实际的频谱分析中，我们往往是不知道频率成分的，但是基于合适的采样率，经过了FFT运算后，可以提取到信号所对应的幅度值、相位、频率，从而我们就可以还原出原始信号所携带的一些频谱成分。

  基于Matlab的FFT数学分析就讲到这里，接下来会详细学习下FFT这个IP核。