T2695 桶哥的问题——吃桶

~~~~~我~是~真的~忍不了~这个~取模~的~锅~了~~~~~

T2695 桶哥的问题——吃桶

前传

1.T2686 桶哥的问题——买桶

这题真的hin简单，真的

2.T2691 桶哥的问题——送桶

前言

这是一道看上去不是毒瘤但实际上有那么一seisei毒瘤的题目

在我多次提交代码仍然屡教不改最后痛改前非的惨痛经历下，总结出以下#￥@￥#%：

1.可以用结构体存 a , b   QAQ实锤啦是取模的锅

不用结构体的话那就换成两个一维数组  a[  ]  b[  ]

2.多取模，越多越好，能往哪里mod就往哪里mod

（一开始mod少了，然后就Wa了）

 解析

1. 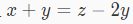        把这个式子化简一下

z - x = 3 y

也就是说明 z，x 属于同一个mod（3）的剩余类

如果 z 是 15 的话，那么 x 可以是 3   6   9   12         （%3……0）

如果 z 是 16 的话，那么 x 可以是 1   4   7   10         （%3…… 1）

如果 z 是 17 的话，那么 x 可以是 2   5   8   11         （%3…… 2）

所以我们就可以枚举 z ，那么符合条件的 x 就是和它同属一个剩余类并且的啦

2.       我们把这个式子拆一下

(  x + z  )·(  b_x - b_z  )

=  x·b_x  +  z·b_x  -  x·b_z  -  z·b_z

所以说，对于每一个 z ，它可以有很多个对应的 x ，虽然 x ，b_x  不确定，但是 z , b_z 是确定的

也就是说对于每一个 z 都可以得到以下这个式子

∑( x·b_x ) +  z·∑b_x  -  b_z·∑x  -  z·b_z·（z的个数）

从前往后枚举 z ，对于每一个 z ，可以满足这个 z 要求的 x 一定也可以满足下一个和这个 z 相类似的 z ，所以说我们就开数组统计一下

S[  ]       到当前为止的满足 z 的 x 的数目

Sx[  ]     到当前为止的满足 z 的 x 的和

Sbx[  ]   到当前为止的满足 z 的 bx 的和

Sxbx[  ]  到当前为止的满足 z 的 x*bx 的和

每次先统计，再更新数组

对于代码当中呢，是枚举三种剩余类，也就是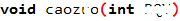  

每次操作之前都要初始化一下

然后开始 for 循环枚举 z ，计算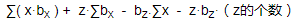 

然后更新数组，按照 a 的种类更新到数组中的不同地方，数组中每一个小格子代表一个种类的桶

注意保证答案不为负数 貌似取模就已经保证了

最后输出答案即可

代码

#include<bits/stdc++.h>

using namespace std;

const int maxn=;
const int mod=;

int n,m;
long long ans;
int S[maxn],Sx[maxn],Sbx[maxn],Sxbx[maxn];

struct RQY
{
    int a,b;
}tong[maxn];

void caozuo(int rqy)
{
    long long hxbx,hzbx,hxbz,hzbz;
    int num=;
    memset(S,,sizeof(S));
    memset(Sx,,sizeof(Sx));
    memset(Sbx,,sizeof(Sbx));
    memset(Sxbx,,sizeof(Sxbx));

    for(int i=rqy;i<=n;i+=)
    {
        num=tong[i].a ;

        hxbx=Sxbx[num]%mod;
        hzbx=i%mod*Sbx[num]%mod;
        hxbz=tong[i].b%mod *Sx[num]%mod;
        hzbz=i%mod*tong[i].b %mod *S[num]%mod;

        ans=(ans+hxbx+hzbx-hxbz-hzbz)%mod;

        S[num]++;
        Sx[num]=(Sx[num]+i%mod)%mod;
        Sbx[num]=(Sbx[num]+tong[i].b%mod)%mod ;
        Sxbx[num]=(Sxbx[num]+i%mod*tong[i].b%mod)%mod ;

    }

}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
      scanf("%d",&tong[i].b );
    for(int i=;i<=n;i++)
      scanf("%d",&tong[i].a );

    caozuo();
    caozuo();
    caozuo();

    while(ans<)
    {
        ans+=mod;
    }

    printf("%ld",ans%mod);

    return ;
}

 题目链接

P2671 求和    

AC的关键    疯狂mod

这个题要注意是枚举2的剩余类啦

~~~~~~QWQ写完之后我发现我要好好组织语言  mod一mod ~~~~~~