[洛谷P1712] NOI2016 区间

问题描述

在数轴上有 n个闭区间 [l1,r1],[l2,r2],...,[ln,rn]。现在要从中选出 m 个区间，使得这 m个区间共同包含至少一个位置。换句话说，就是使得存在一个 x，使得对于每一个被选中的区间 [li,ri]，都有 li≤x≤ri。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 [li,ri] 的长度定义为 ri−li，即等于它的右端点的值减去左端点的值。

输入格式

第一行包含两个正整数 n,m用空格隔开，意义如上文所述。保证 1≤m≤n

接下来 n行，每行表示一个区间，包含用空格隔开的两个整数 li 和 ri 为该区间的左右端点。

N<=500000,M<=200000,0≤li≤ri≤10^9

输出格式

只有一行，包含一个正整数，即最小花费。

样例输入

6 3

3 5

1 2

3 4

2 2

1 5

1 4

样例输出

2

说明

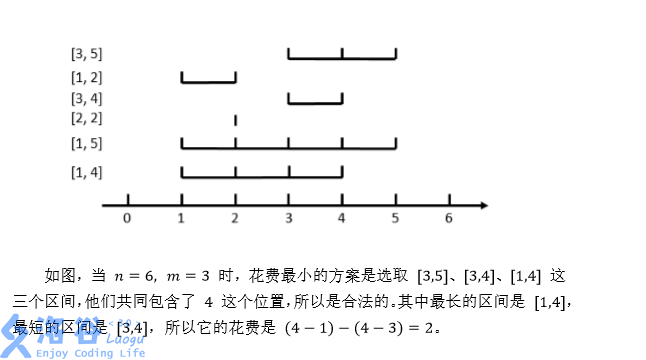
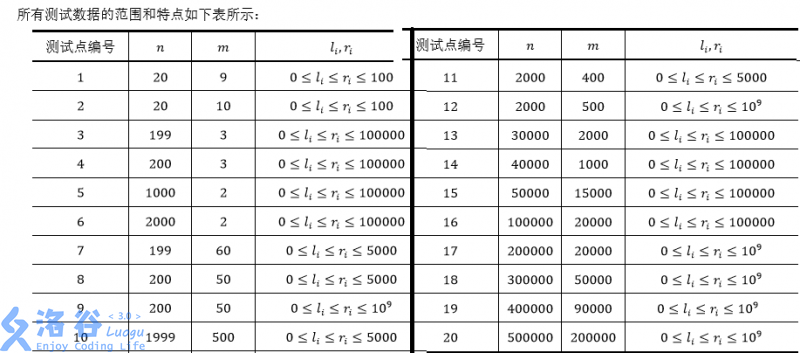
解析

我们尽可能地要取费用小的区间，所以就把所有的区间按长度从小到大排序。利用尺取法的思想，逐个加入区间。若某个时刻某个点被覆盖的次数大于m，统计答案，然后就从前面开始去掉区间直到覆盖次数小于等于m。 具体维护可以用线段树维护覆盖次数的最大值来做。当然l和r是要离散化的。

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#define N 500002
using namespace std;
struct seg{
	int len,l,r;
}a[N];
struct SegmentTree{
	int dat,add;
}t[N*8];
int n,m,i,j,tmp[N*2];
int read()
{
	char c=getchar();
	int w=0;
	while(c<'0'||c>'9') c=getchar();
	while(c<='9'&&c>='0'){
		w=w*10+c-'0';
		c=getchar();
	}
	return w;
}
int my_comp(const seg &x,const seg &y)
{
	return x.len<y.len;
}
void spread(int p)
{
	if(t[p].add){
		t[p*2].dat+=t[p].add;
		t[p*2+1].dat+=t[p].add;
		t[p*2].add+=t[p].add;
		t[p*2+1].add+=t[p].add;
		t[p].add=0;
	}
}
void change(int p,int l,int r,int ql,int qr,int x)
{
	if(ql<=l&&r<=qr){
		t[p].dat+=x;
		t[p].add+=x;
		return;
	}
	int mid=(l+r)/2;
	spread(p);
	if(ql<=mid) change(p*2,l,mid,ql,qr,x);
	if(qr>mid) change(p*2+1,mid+1,r,ql,qr,x);
	t[p].dat=max(t[p*2].dat,t[p*2+1].dat);
}
int main()
{
	n=read();m=read();
	for(i=1;i<=n;i++){
		a[i].l=read(),a[i].r=read();
		tmp[i*2-1]=a[i].l;
		tmp[i*2]=a[i].r;
	}
	sort(tmp+1,tmp+2*n+1);
	int n1=unique(tmp+1,tmp+2*n+1)-tmp-1;
	for(i=1;i<=n;i++){
		a[i].len=a[i].r-a[i].l;
		a[i].l=lower_bound(tmp+1,tmp+n1+1,a[i].l)-tmp;
		a[i].r=lower_bound(tmp+1,tmp+n1+1,a[i].r)-tmp;
	}
	sort(a+1,a+n+1,my_comp);
	i=j=0;
	int ans=1<<30;
	while(i<n){
		while(i<n&&t[1].dat<m){
			i++;
			change(1,1,n1,a[i].l,a[i].r,1);
		}
		if(t[1].dat<m) break;
		while(j<n&&t[1].dat>=m){
			j++;
			change(1,1,n1,a[j].l,a[j].r,-1);
		}
		ans=min(ans,a[i].len-a[j].len);
	}
	if(ans==1<<30) printf("-1\n");
	else printf("%d\n",ans);
	return 0;
}