NLP（二十九）一步一步，理解Self-Attention

本文大部分内容翻译自Illustrated Self-Attention, Step-by-step guide to self-attention with illustrations and code，仅用于学习，如有翻译不当之处，敬请谅解！

什么是Self-Attention（自注意力机制）？

如果你在想Self-Attention（自注意力机制）是否和Attention（注意力机制）相似，那么答案是肯定的。它们本质上属于同一个概念，拥有许多共同的数学运算。

一个Self-Attention模块拥有n个输入，返回n个输出。这么模块里面发生了什么？从非专业角度看，Self-Attention（自注意力机制）允许输入之间互相作用（“self”部分），寻找出谁更应该值得注意（“attention”部分）。输出的结果是这些互相作用和注意力分数的聚合。

一步步理解Self-Attention

理解分为以下几步：

准备输入；
初始化权重；
获取key，query和value；
为第1个输入计算注意力分数；
计算softmax;
将分数乘以values；
对权重化后的values求和，得到输出1；
对其余的输入，重复第4-7步。

注意：实际上，这些数学运算都是向量化的，也就是说，所有的输入都会一起经历这些数学运算。我们将会在后面的代码部分看到。

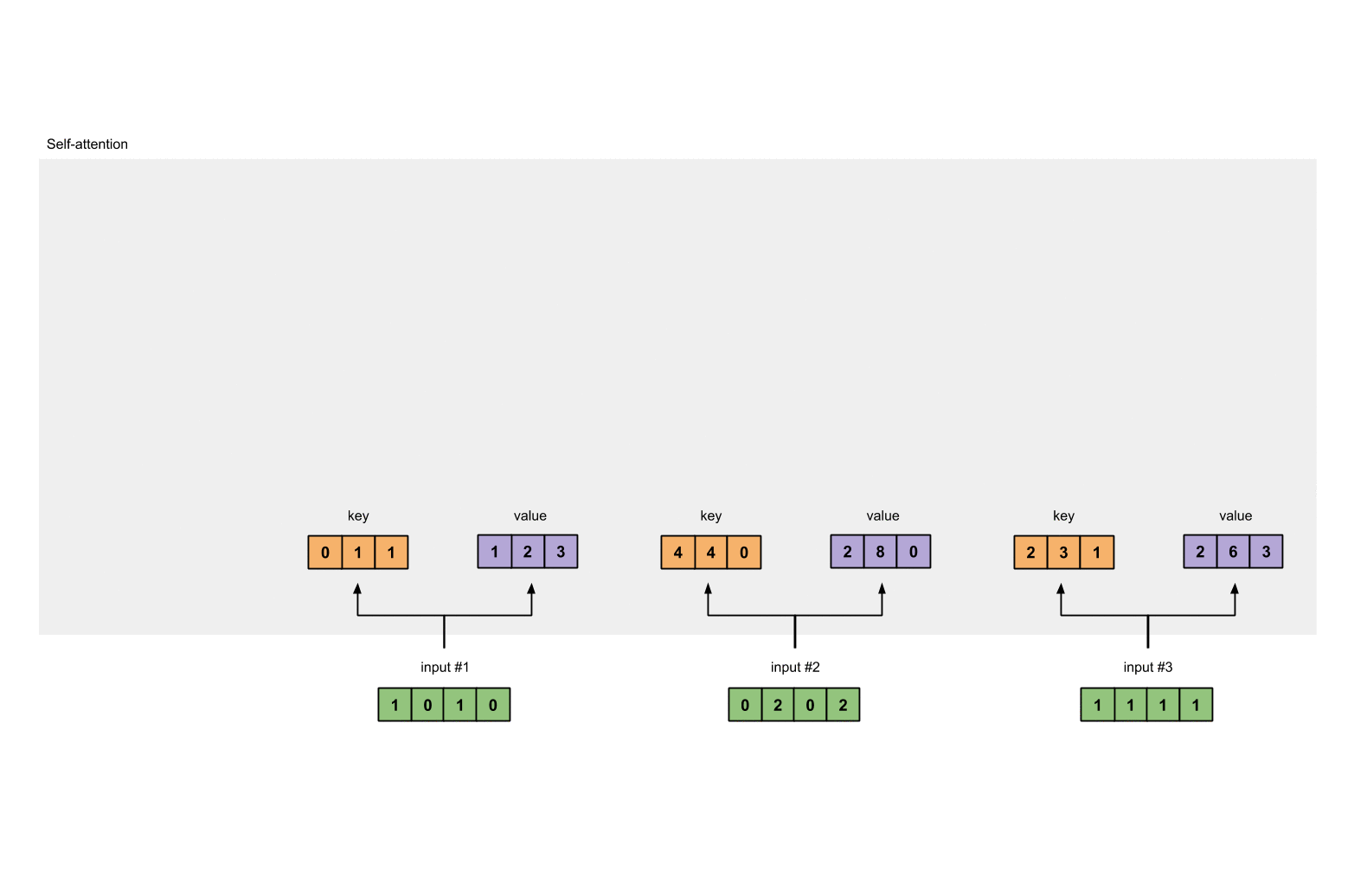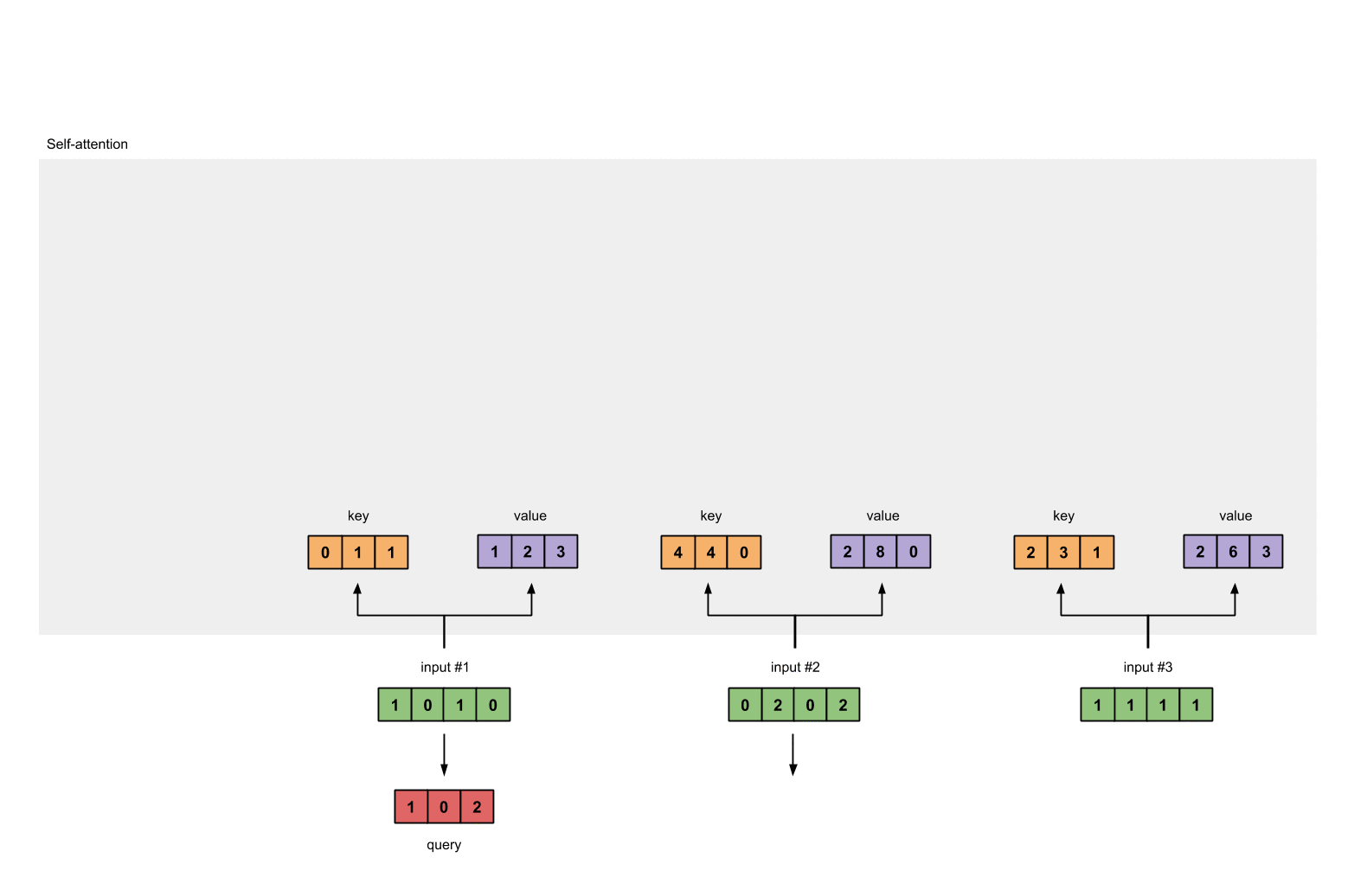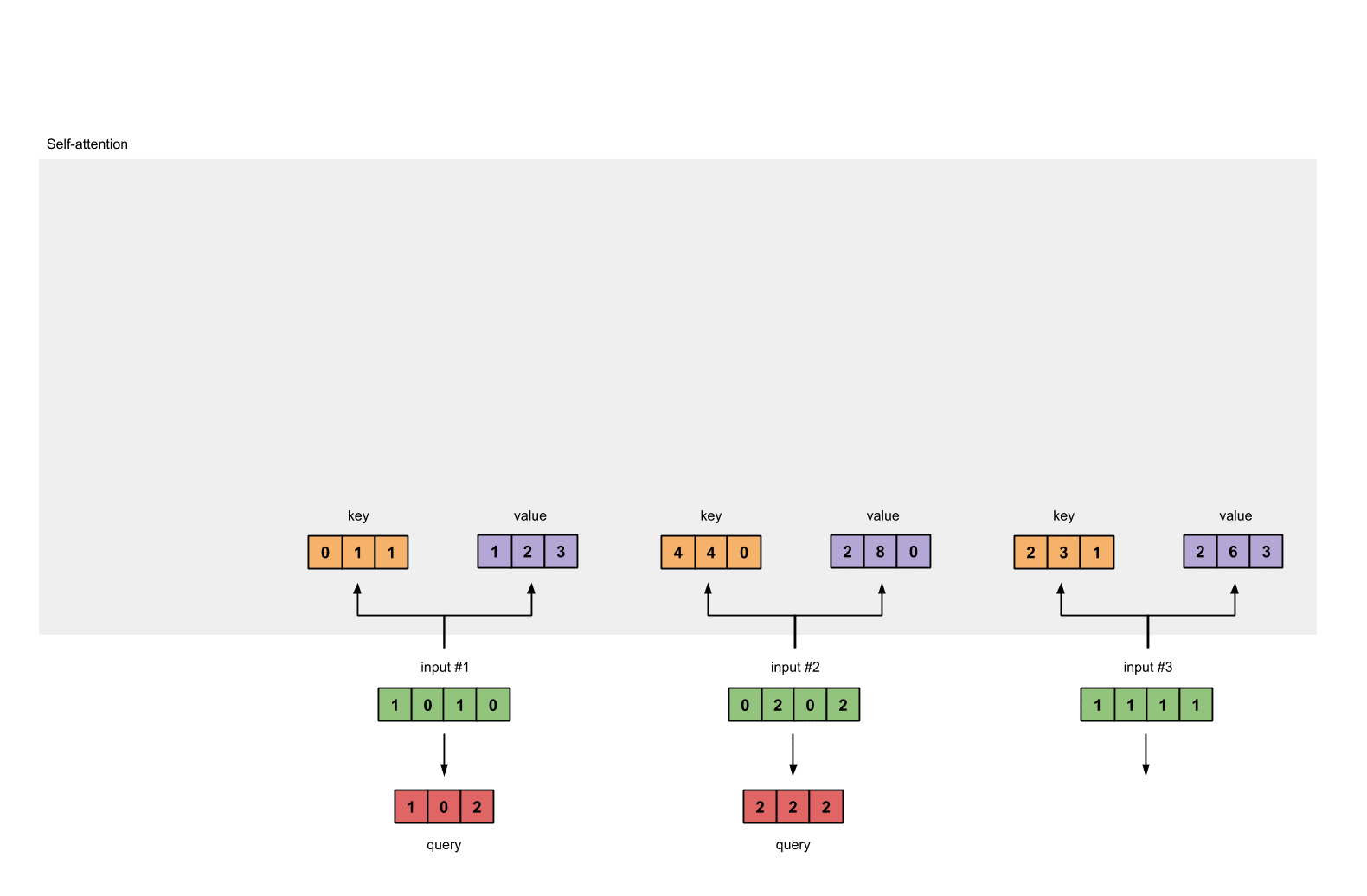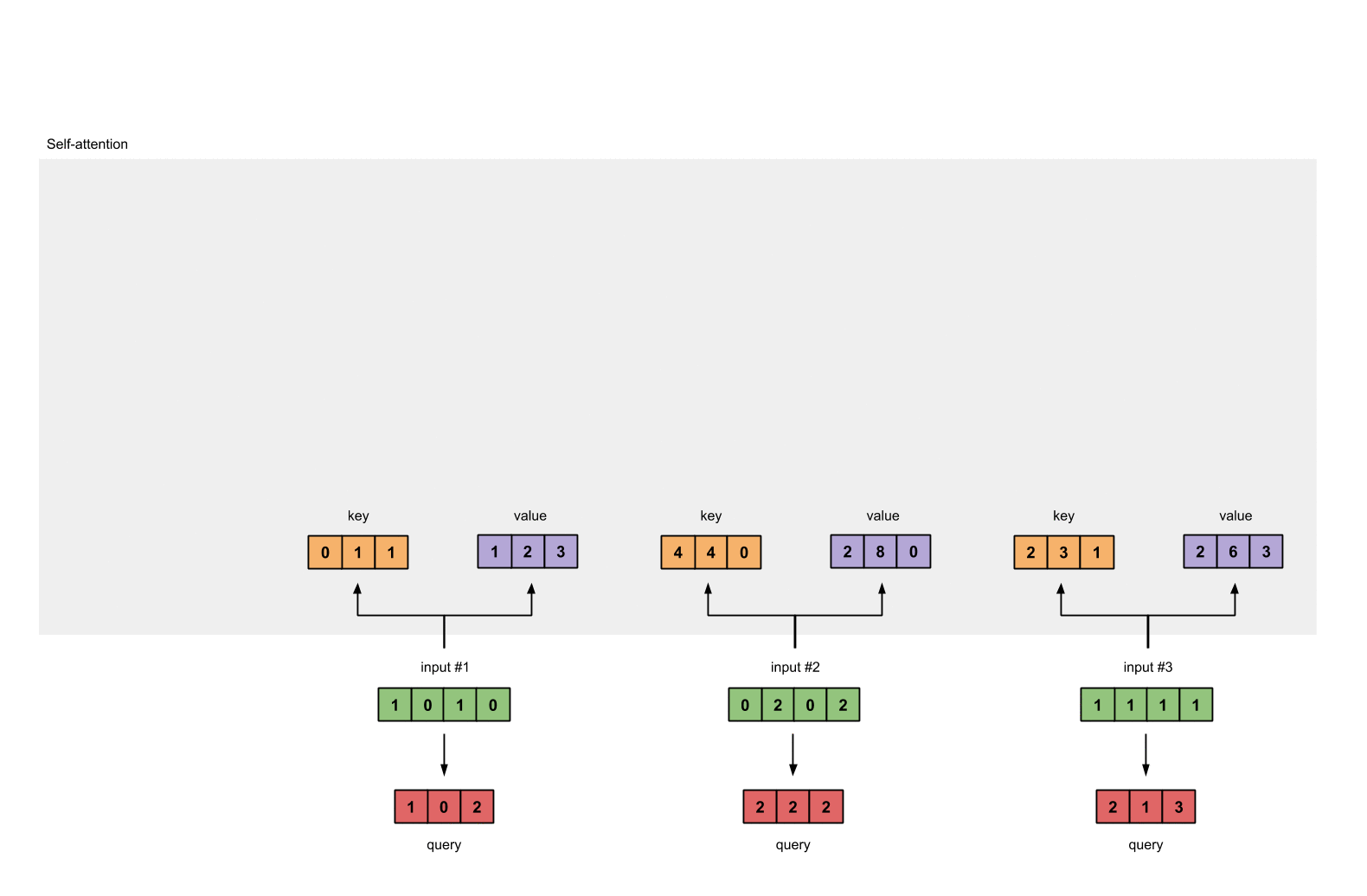
第一步：准备输入

在这个教程中，我们从3个输入开始，每个输入的维数为4。

Input 1: [1, 0, 1, 0]

Input 2: [0, 2, 0, 2]

Input 3: [1, 1, 1, 1]

第二步：初始化权重

每个输入必须由三个表示（看下图）。这些输入被称作key（橙色），query（红色）value（紫色）。在这个例子中，我们假设我们想要的表示维数为3。因为每个输入的维数为4，这就意味着每个权重的形状为4×3。

注意：我们稍后会看到value的维数也是output的维数。

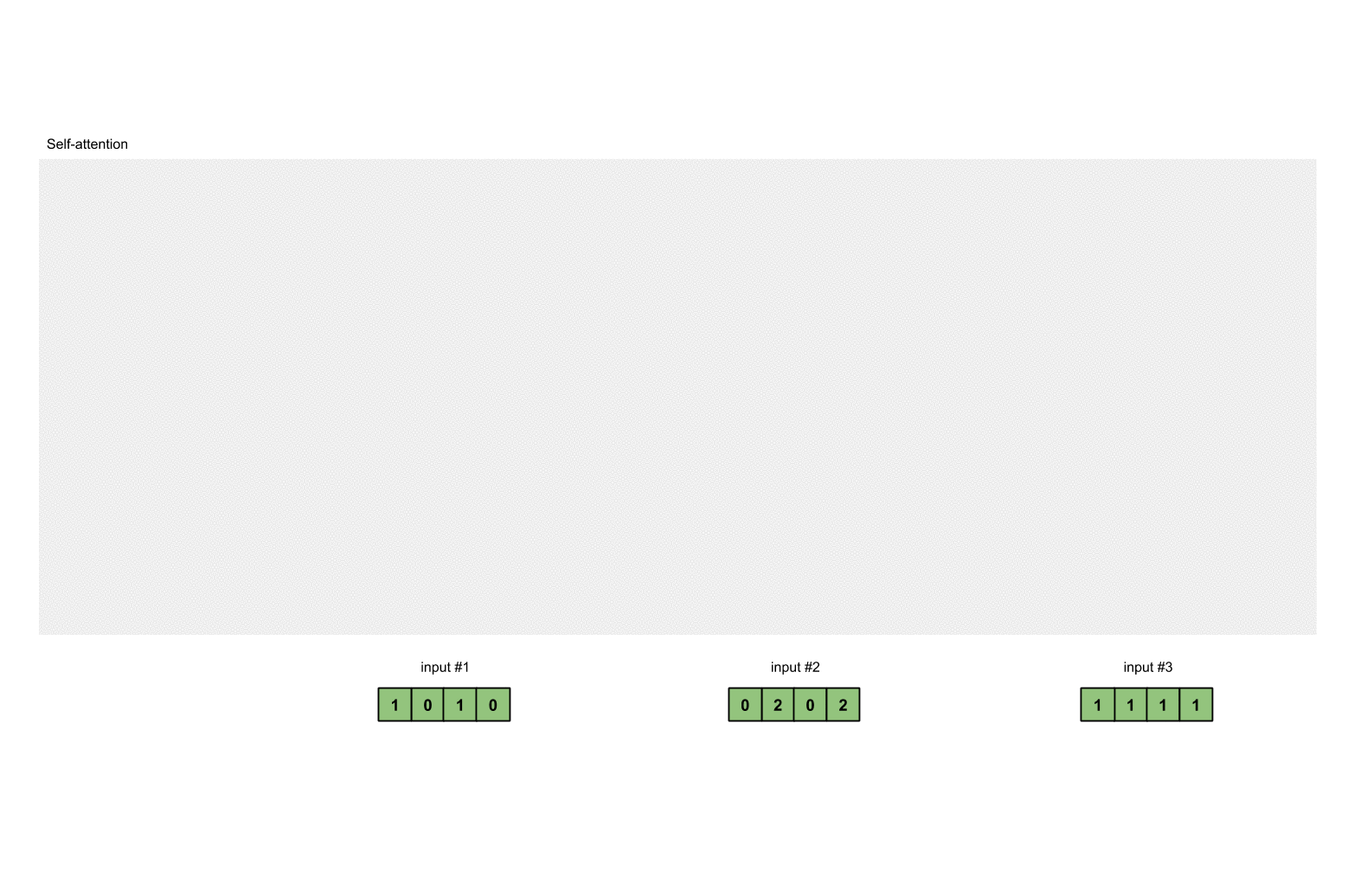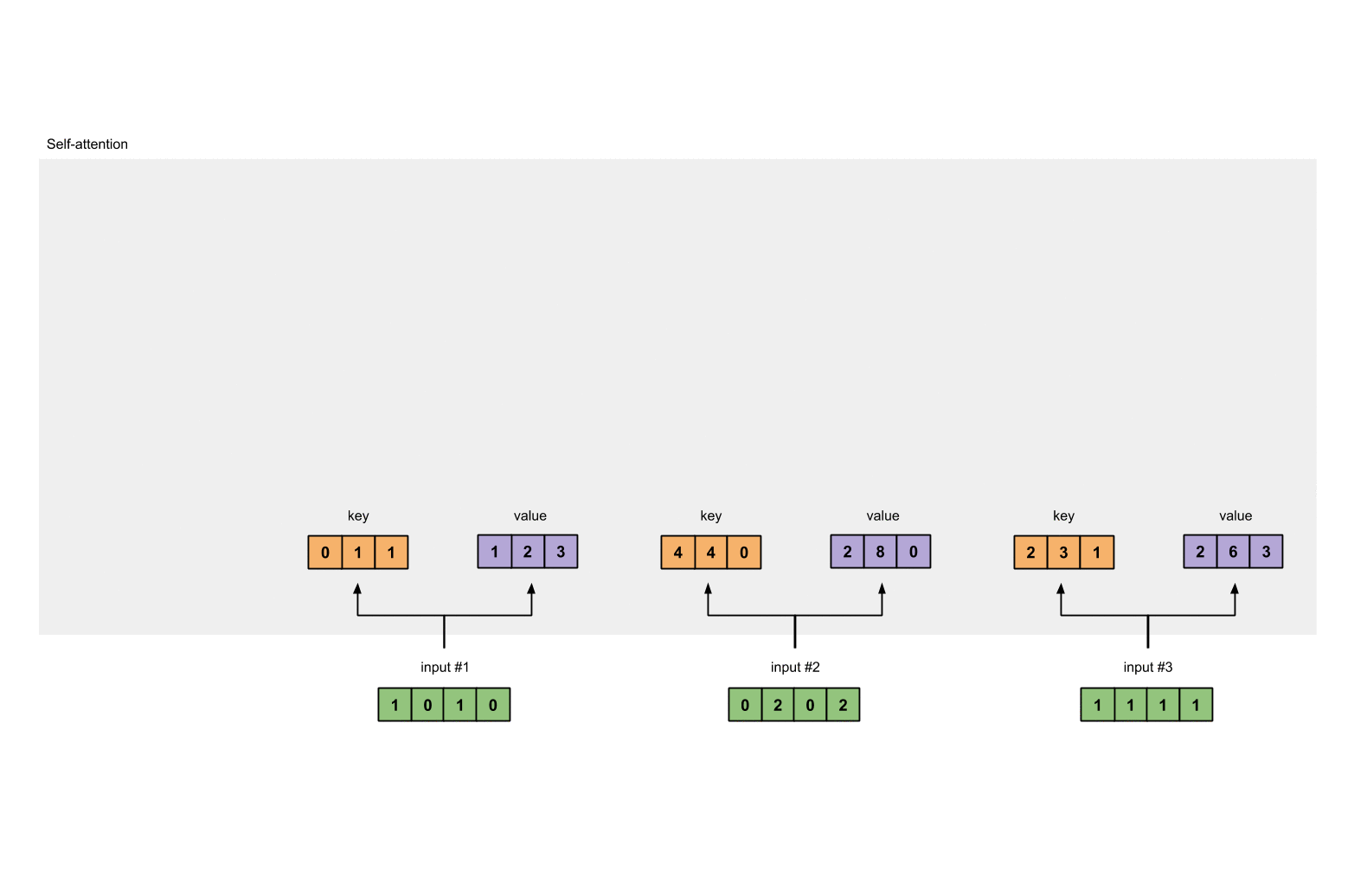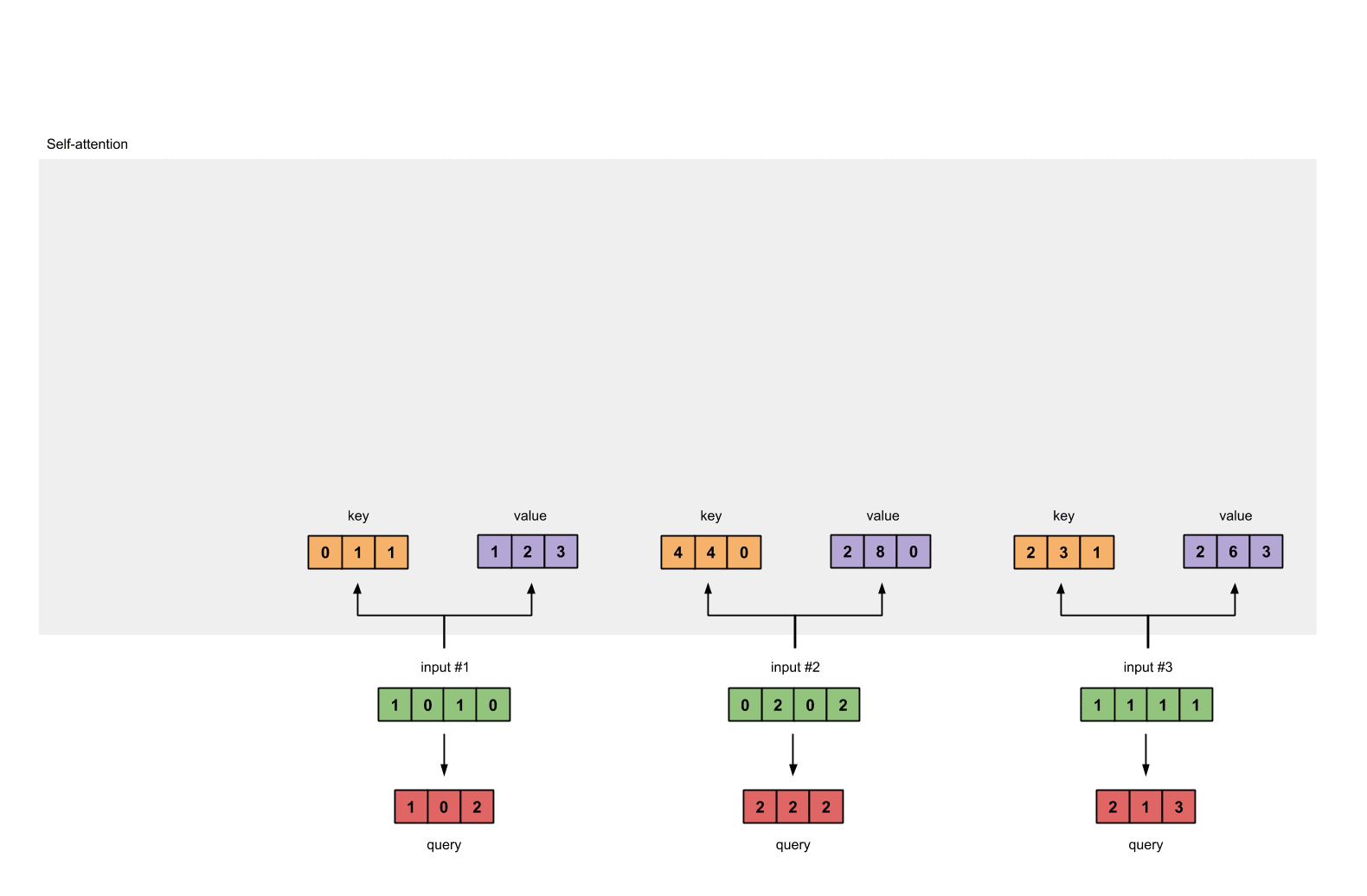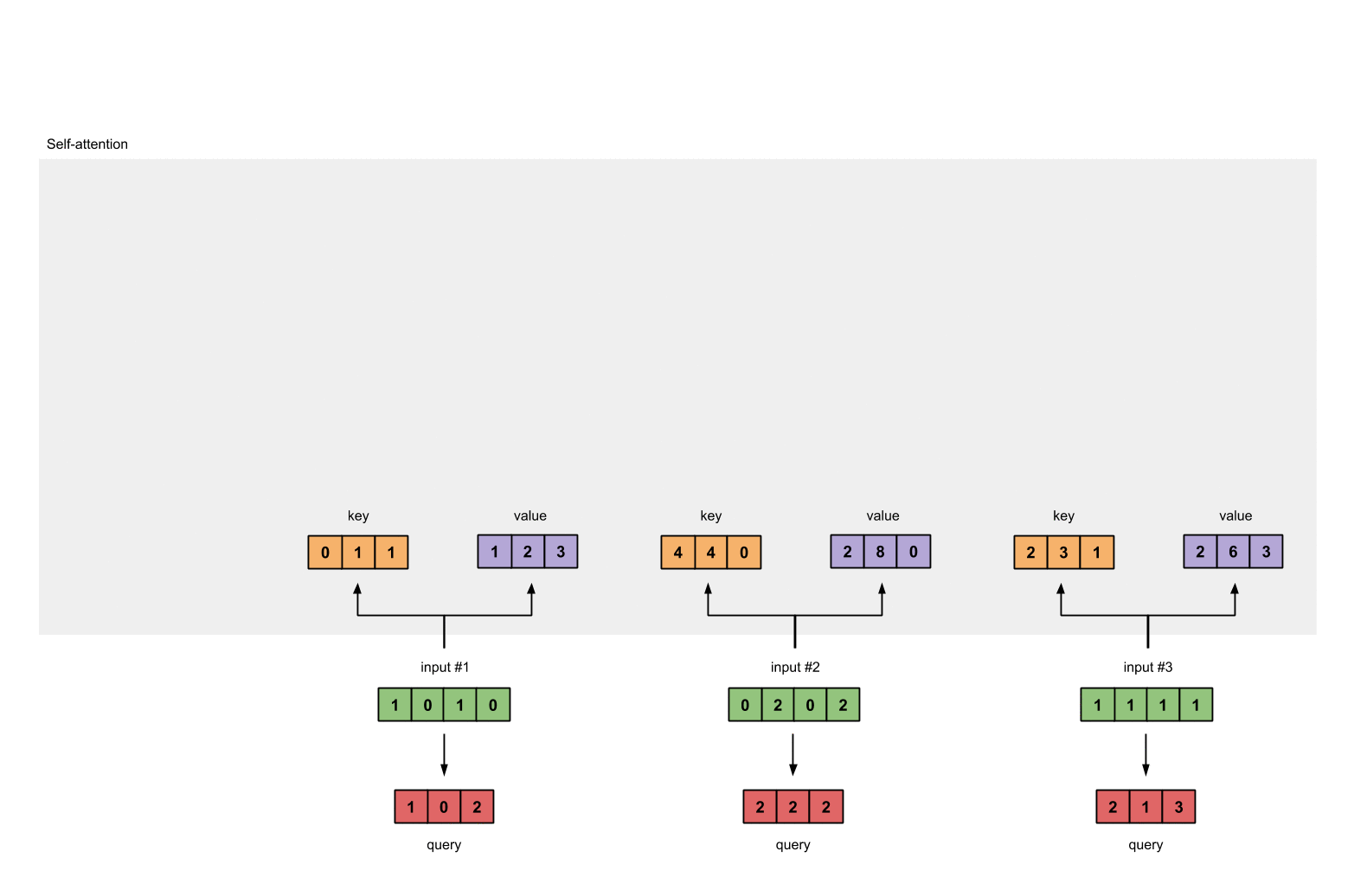
为了获取这些表示，每个输入（绿色）会乘以一个权重的集合得到keys，乘以一个权重的集合得到queries，乘以一个权重的集合得到values。在我们的例子中，我们初始化三个权重的集合如下。

key的权重：

[[0, 0, 1],

 [1, 1, 0],

 [0, 1, 0],

 [1, 1, 0]]

query的权重：

[[1, 0, 1],

 [1, 0, 0],

 [0, 0, 1],

 [0, 1, 1]]

value的权重：

[[0, 2, 0],

 [0, 3, 0],

 [1, 0, 3],

 [1, 1, 0]]

注意：在神经网络设置中，这些权重通常都是一些小的数字，利用随机分布，比如Gaussian, Xavier and Kaiming分布，随机初始化。在训练开始前已经完成初始化。

第三步：获取`key`，`query`和`value`；

现在我们有了3个权重的集合，让我们来给每个输入获取key，query和value。

第1个输入的key表示：

               [0, 0, 1]

[1, 0, 1, 0] x [1, 1, 0] = [0, 1, 1]

               [0, 1, 0]

               [1, 1, 0]

利用相同的权重集合获取第2个输入的key表示：

               [0, 0, 1]

[0, 2, 0, 2] x [1, 1, 0] = [4, 4, 0]

               [0, 1, 0]

               [1, 1, 0]

利用相同的权重集合获取第3个输入的key表示：

               [0, 0, 1]

[1, 1, 1, 1] x [1, 1, 0] = [2, 3, 1]

               [0, 1, 0]

               [1, 1, 0]

更快的方式是将这些运算用向量来描述：

               [0, 0, 1]

[1, 0, 1, 0]   [1, 1, 0]   [0, 1, 1]

[0, 2, 0, 2] x [0, 1, 0] = [4, 4, 0]

[1, 1, 1, 1]   [1, 1, 0]   [2, 3, 1]

让我们用相同的操作来获取每个输入的value表示：

最后是query的表示：

               [1, 0, 1]

[1, 0, 1, 0]   [1, 0, 0]   [1, 0, 2]

[0, 2, 0, 2] x [0, 0, 1] = [2, 2, 2]

[1, 1, 1, 1]   [0, 1, 1]   [2, 1, 3]

注意：实际上，一个偏重向量也许会加到矩阵相乘后的结果。

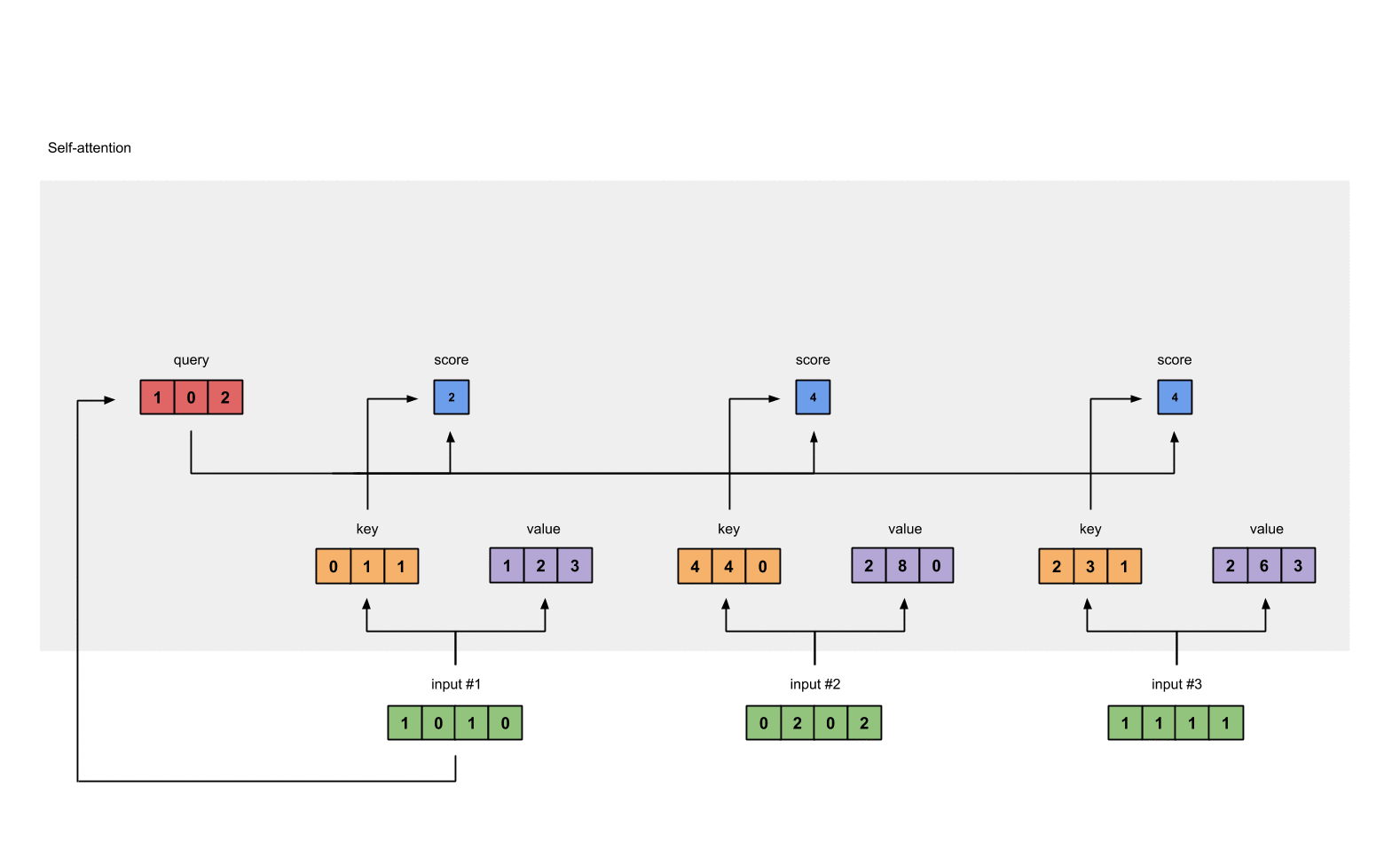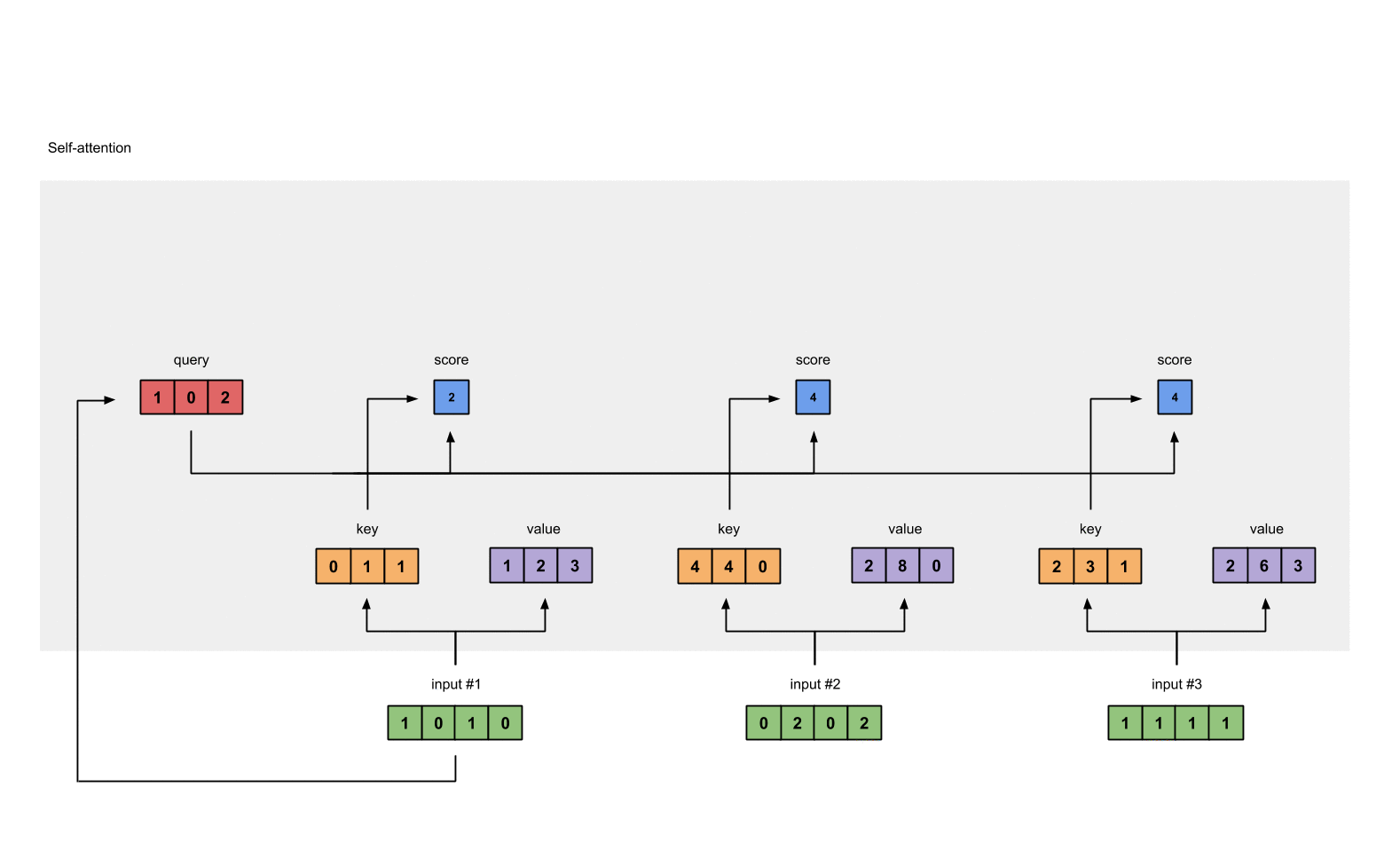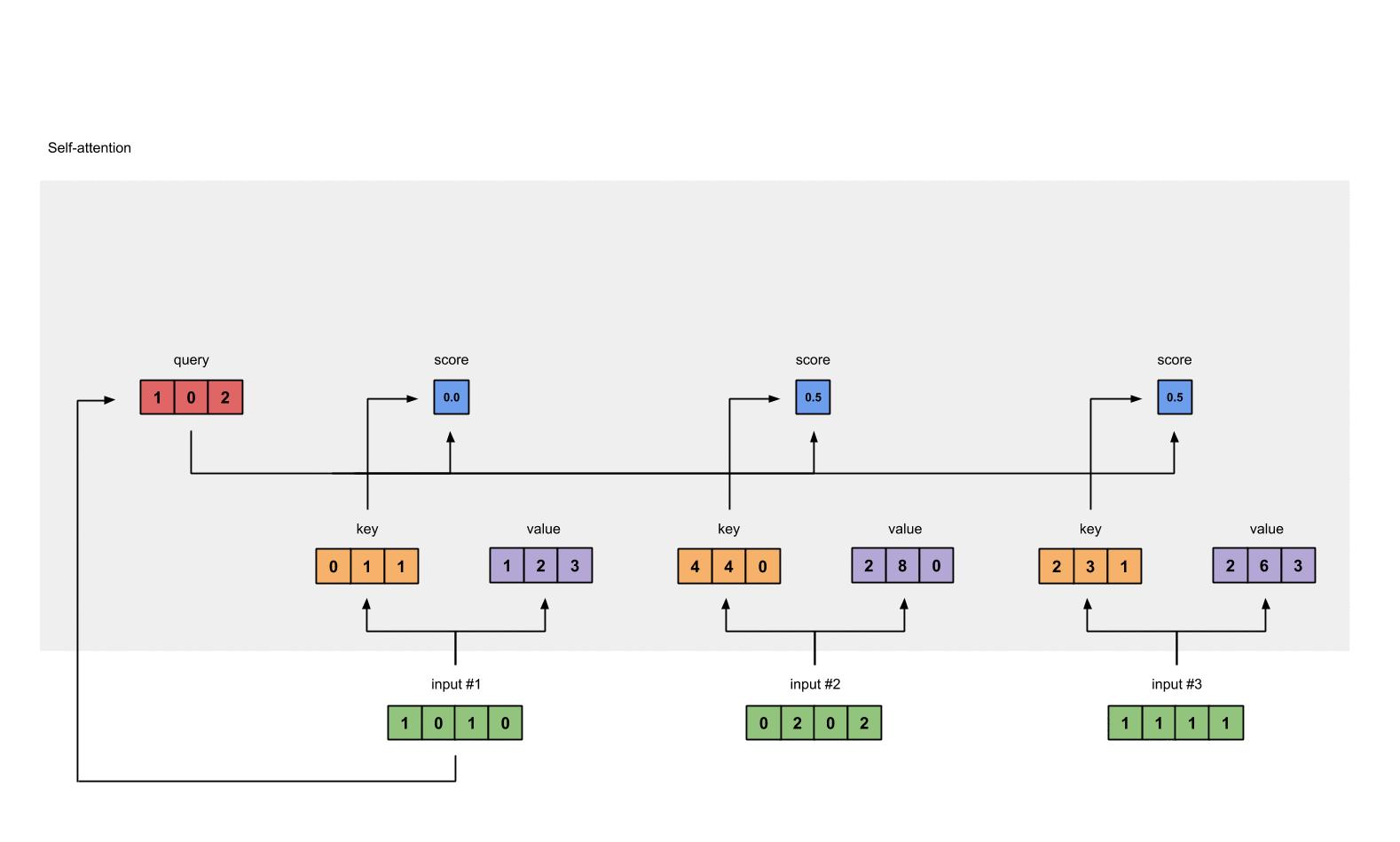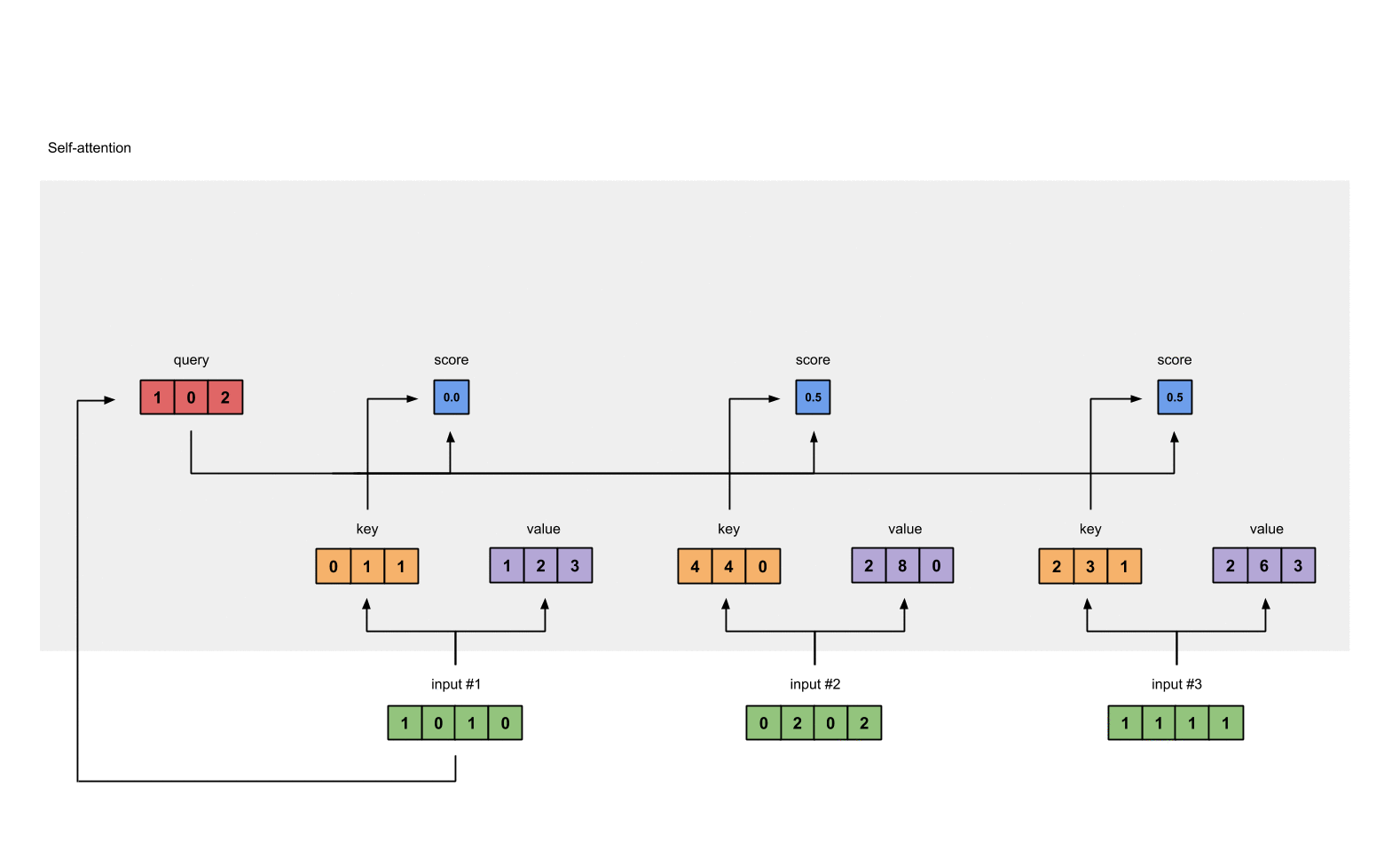
第四步：为第1个输入计算注意力分数

为了获取注意力分数，我们从输入1的query（红色）和所有keys（橙色）的点积开始。因为有3个key表示（这是由于我们有3个输入），我们得到3个注意力分数（蓝色）。

            [0, 4, 2]

[1, 0, 2] x [1, 4, 3] = [2, 4, 4]

            [1, 0, 1]

注意到我们只用了输入的query。后面我们会为其他的queries重复这些步骤。

第五步：计算softmax

对这些注意力分数进行softmax函数运算（蓝色部分）。

softmax([2, 4, 4]) = [0.0, 0.5, 0.5]

第六步：将分数乘以values

将每个输入（绿色）的softmax作用后的注意力分数乘以各自对应的value（紫色）。这会产生3个向量（黄色）。在这个教程中，我们把它们称作权重化value。

1: 0.0 * [1, 2, 3] = [0.0, 0.0, 0.0]

2: 0.5 * [2, 8, 0] = [1.0, 4.0, 0.0]

3: 0.5 * [2, 6, 3] = [1.0, 3.0, 1.5]

第七步：对权重化后的values求和，得到输出1

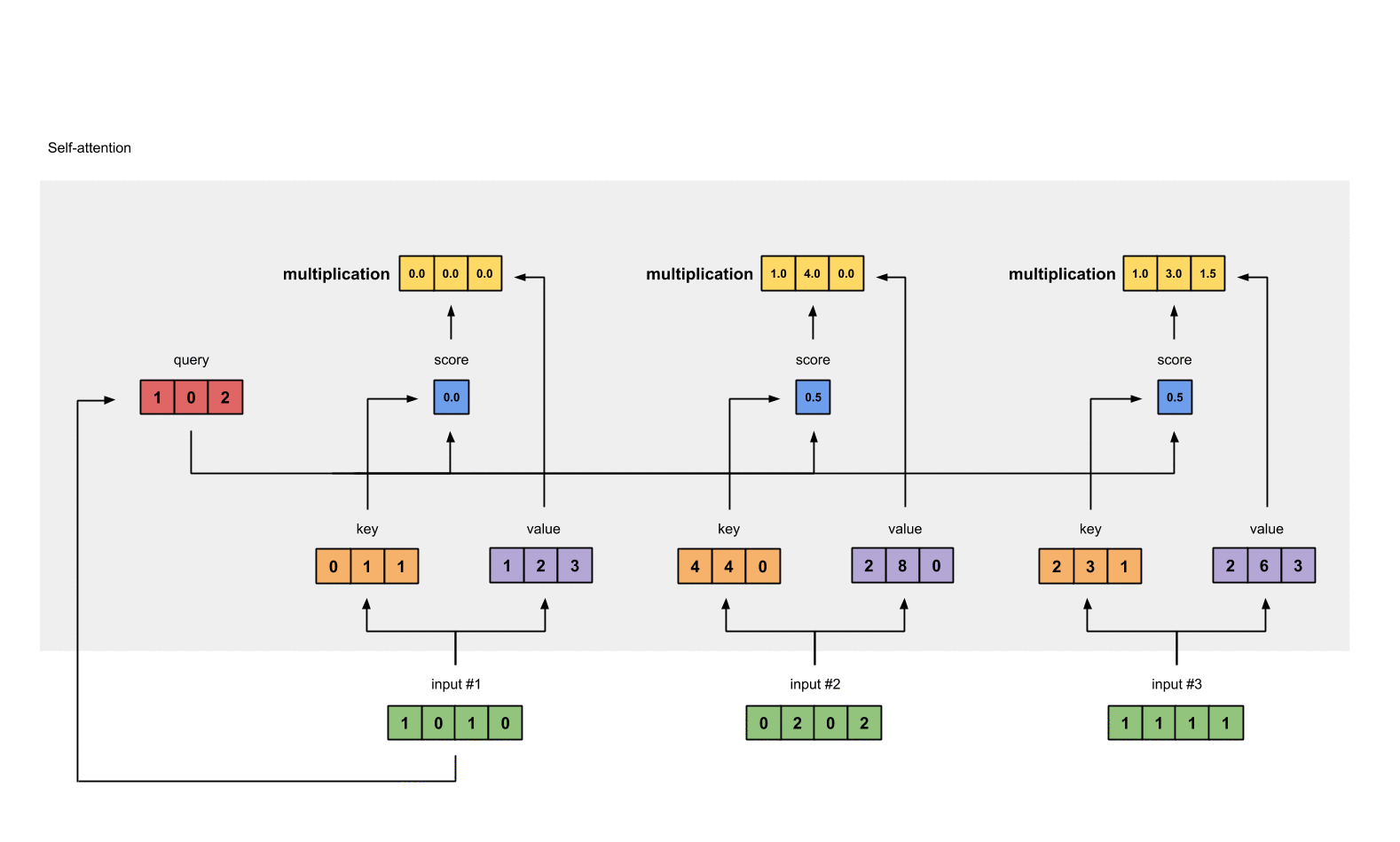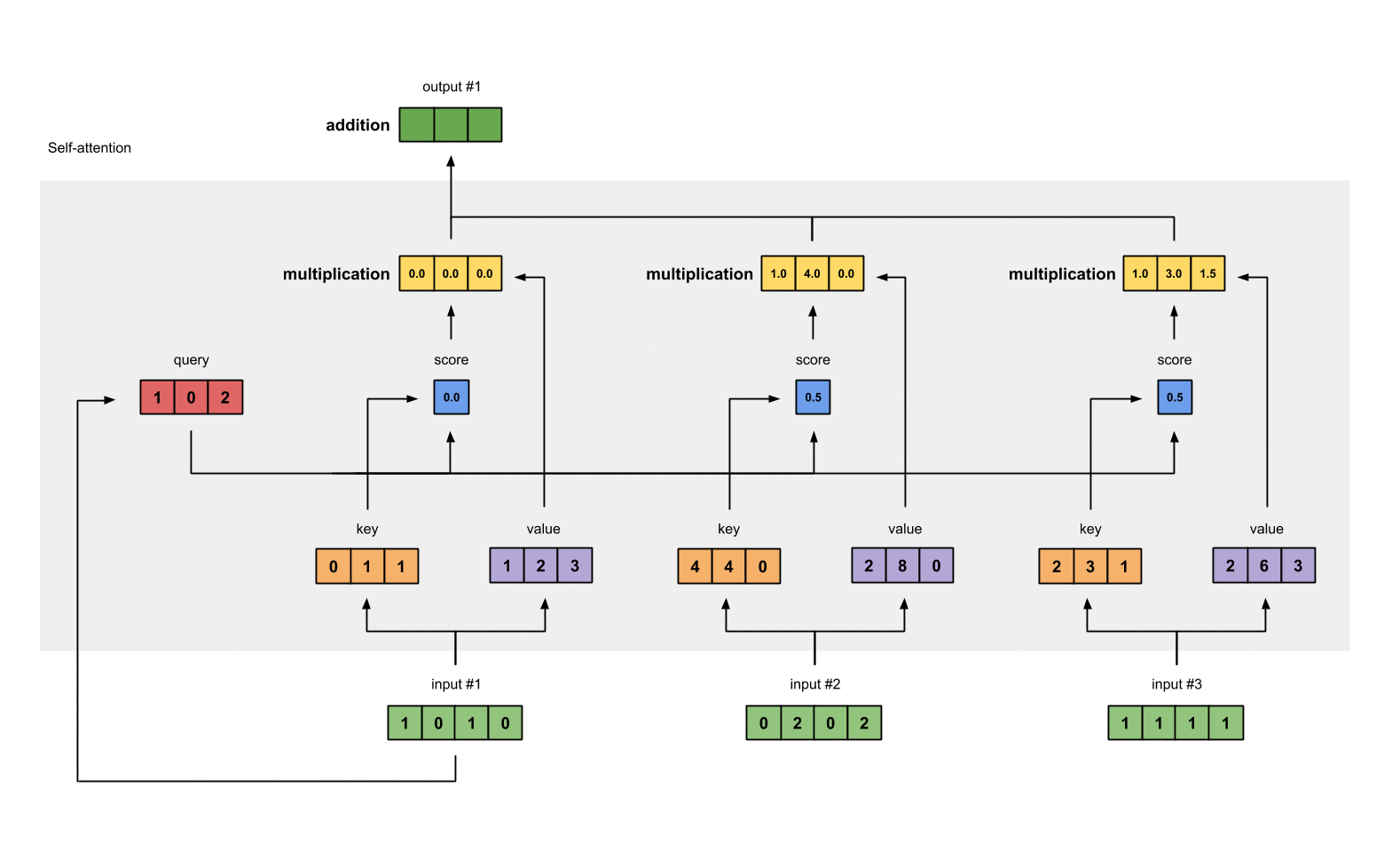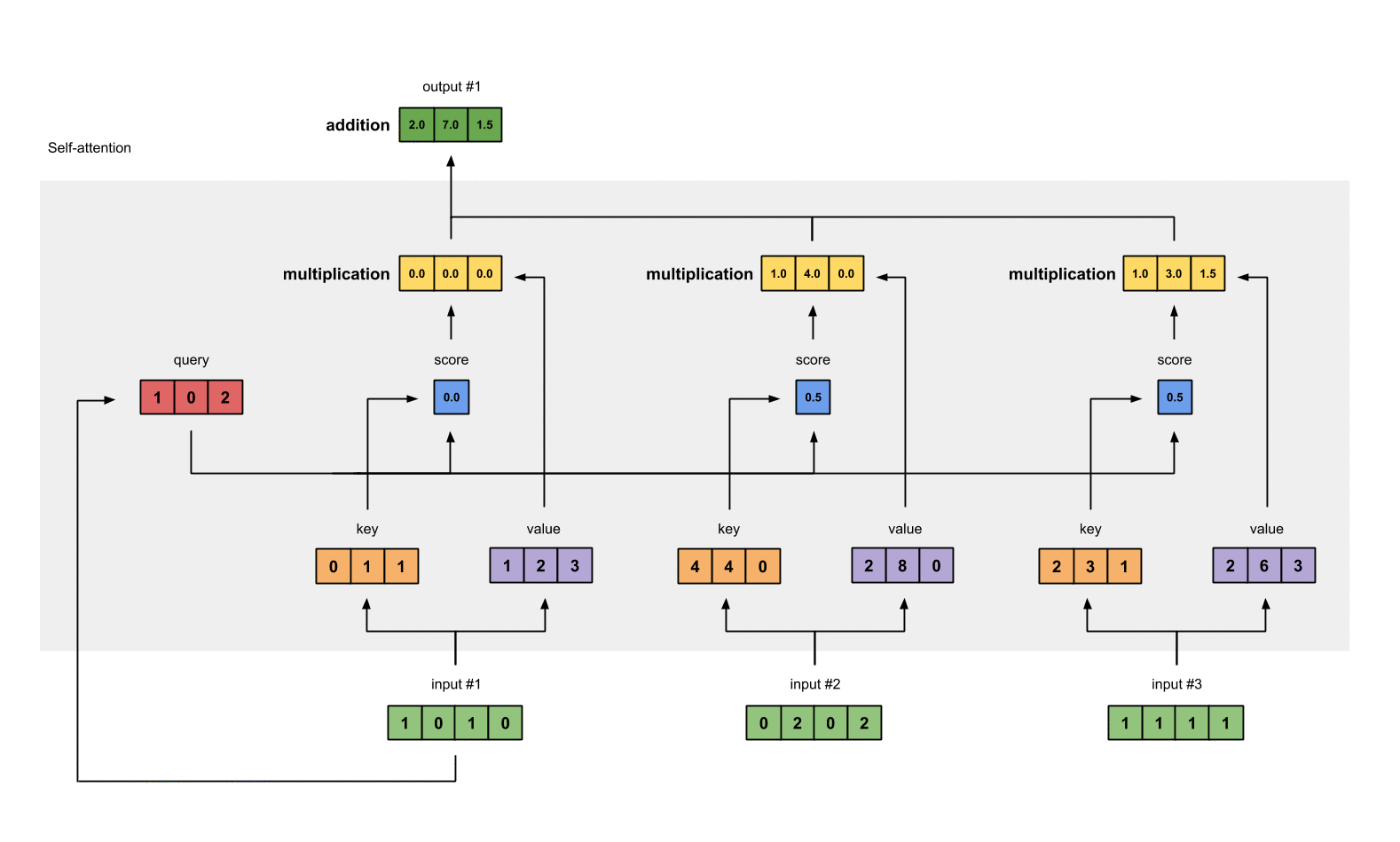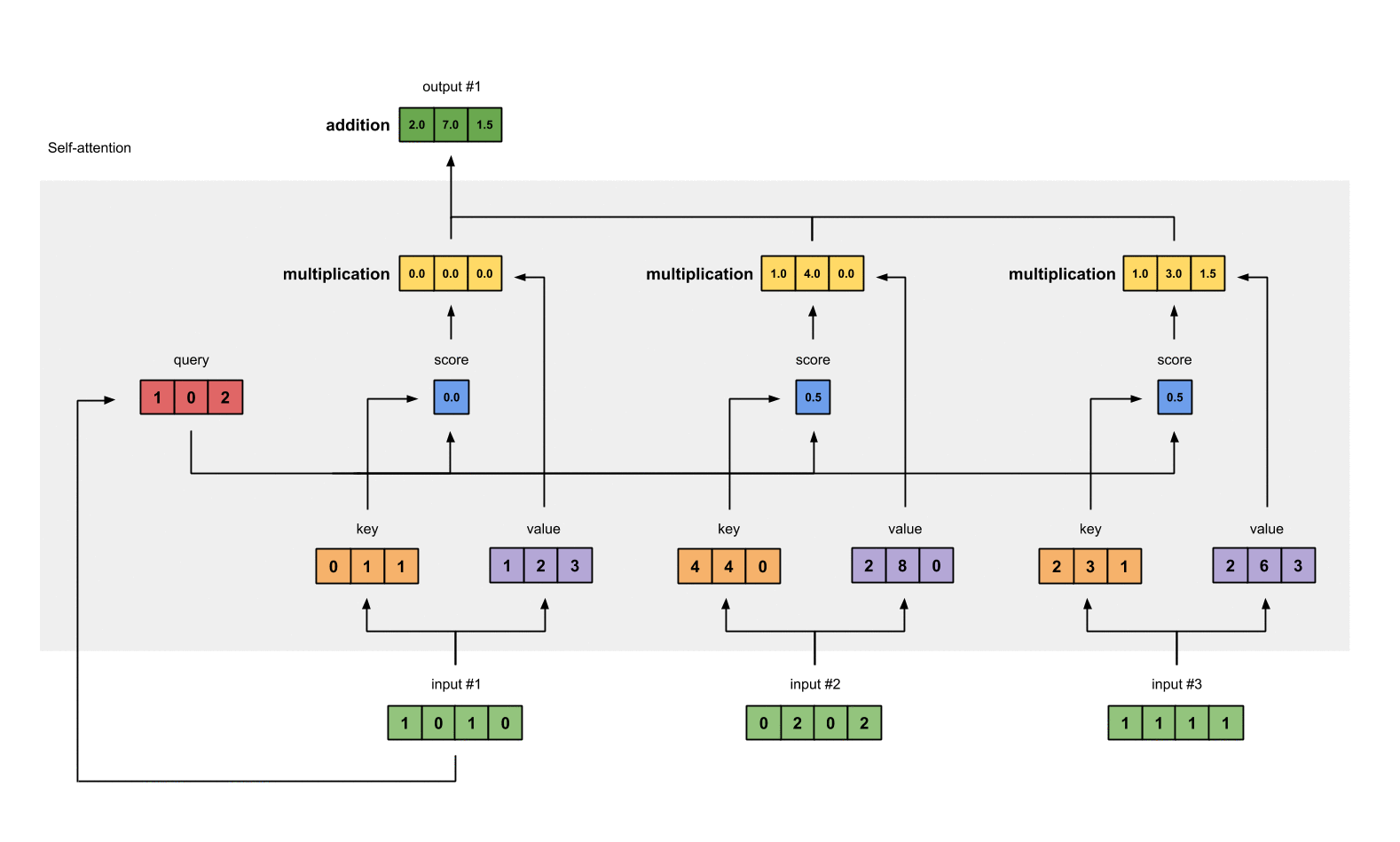
将权重后value按元素相加得到输出1：

  [0.0, 0.0, 0.0]

+ [1.0, 4.0, 0.0]

+ [1.0, 3.0, 1.5]

-----------------

= [2.0, 7.0, 1.5]

产生的向量[2.0, 7.0, 1.5]（暗绿色）就是输出1，这是基于输入1的query表示与其它的keys，包括它自身的key互相作用的结果。

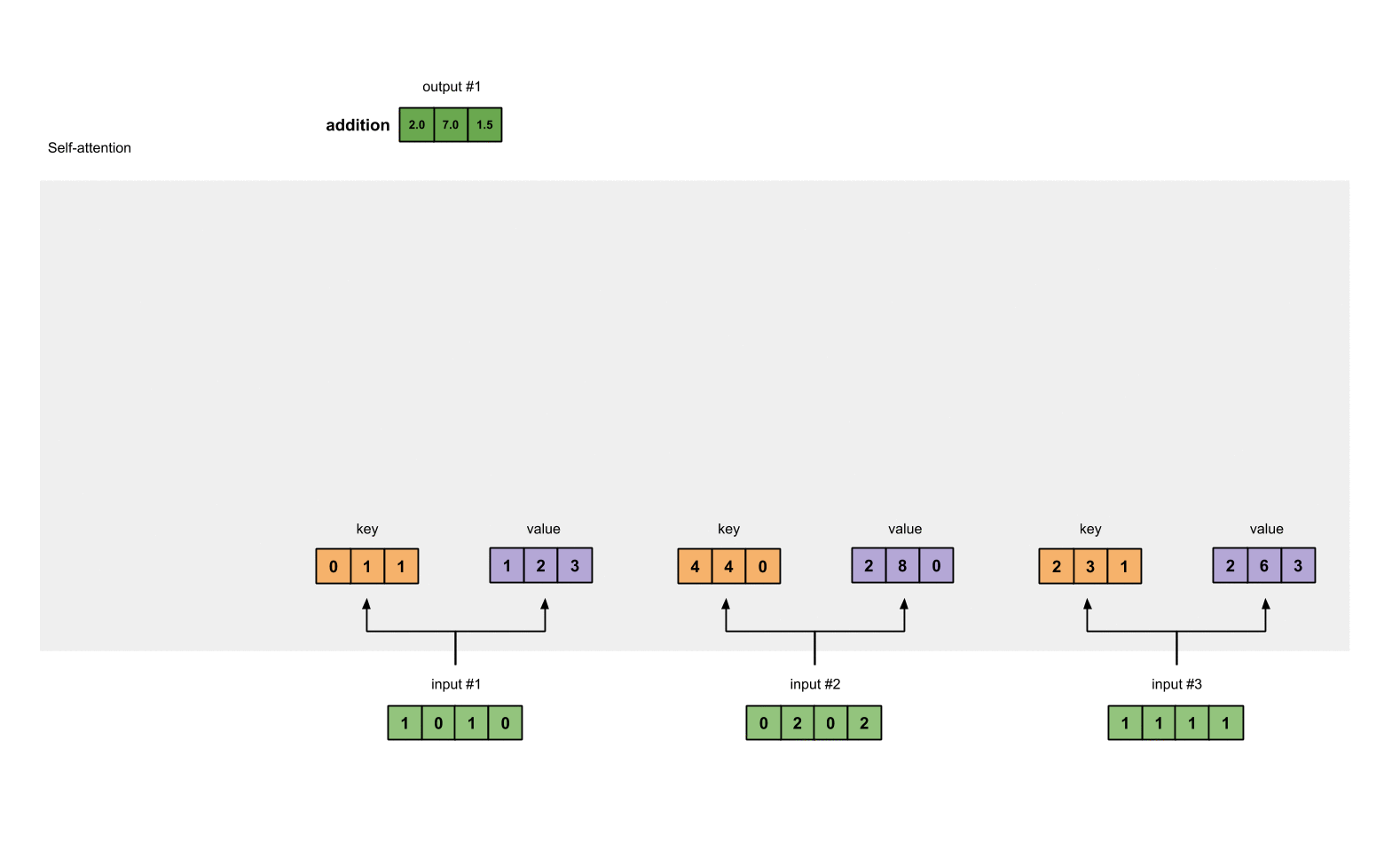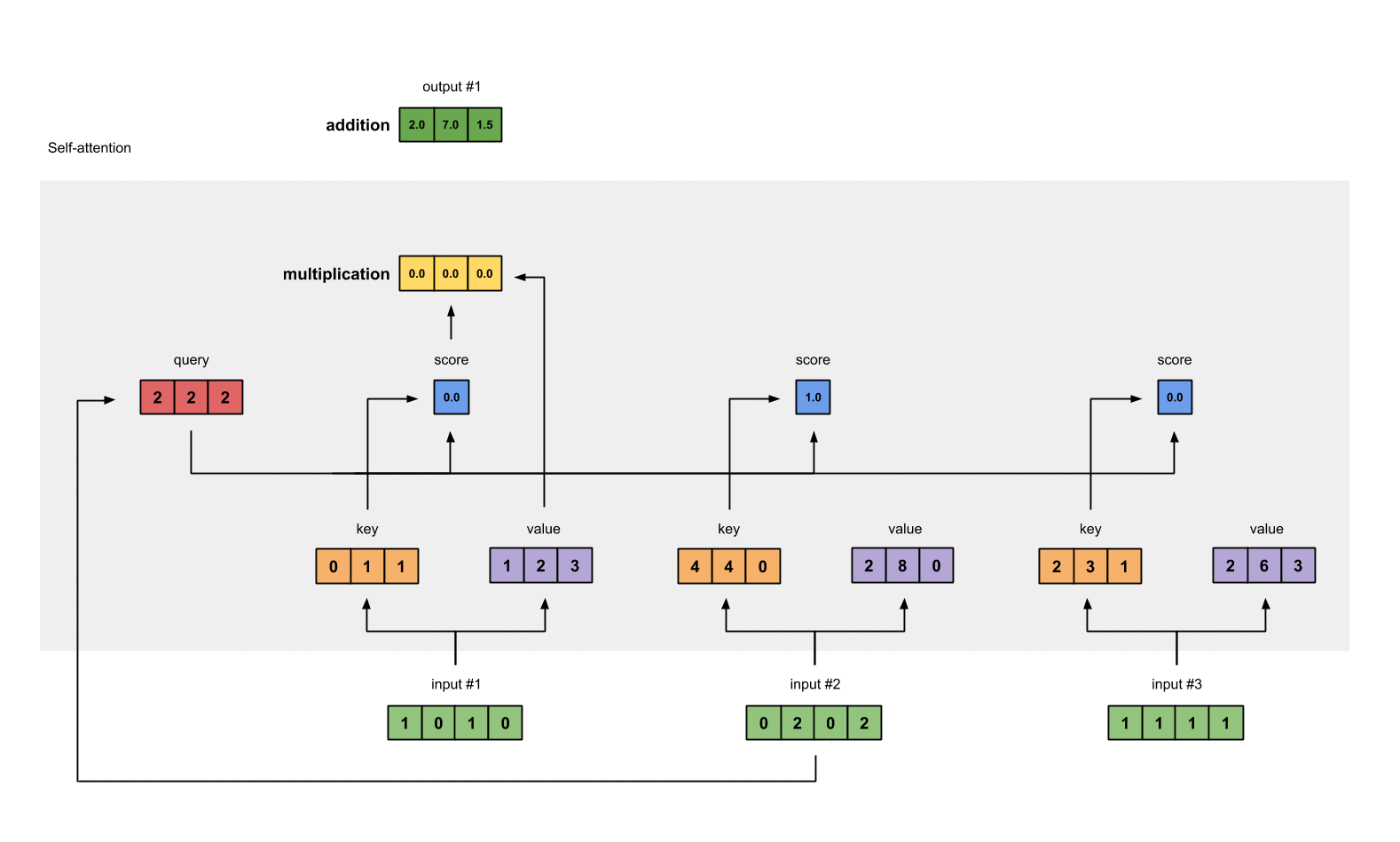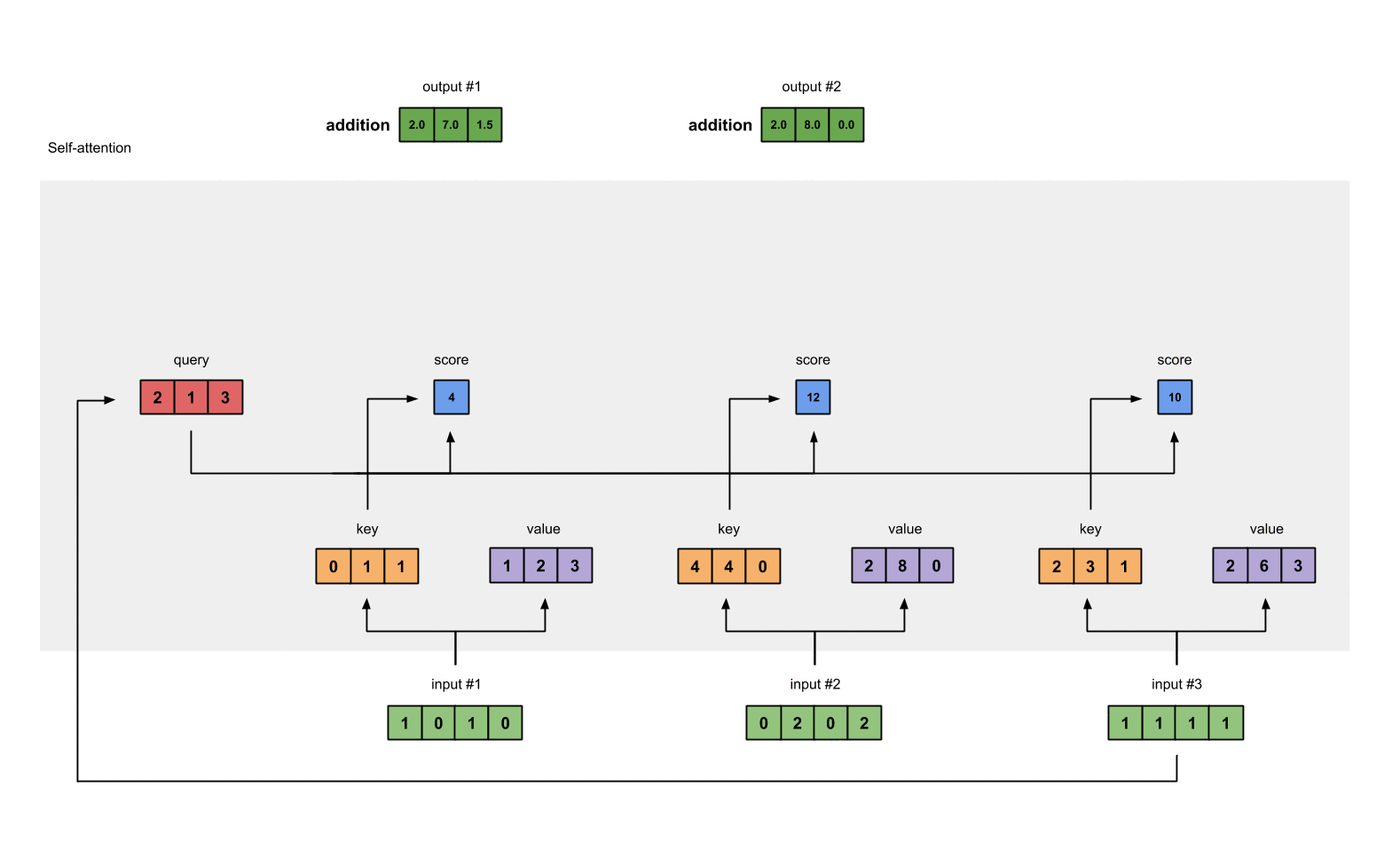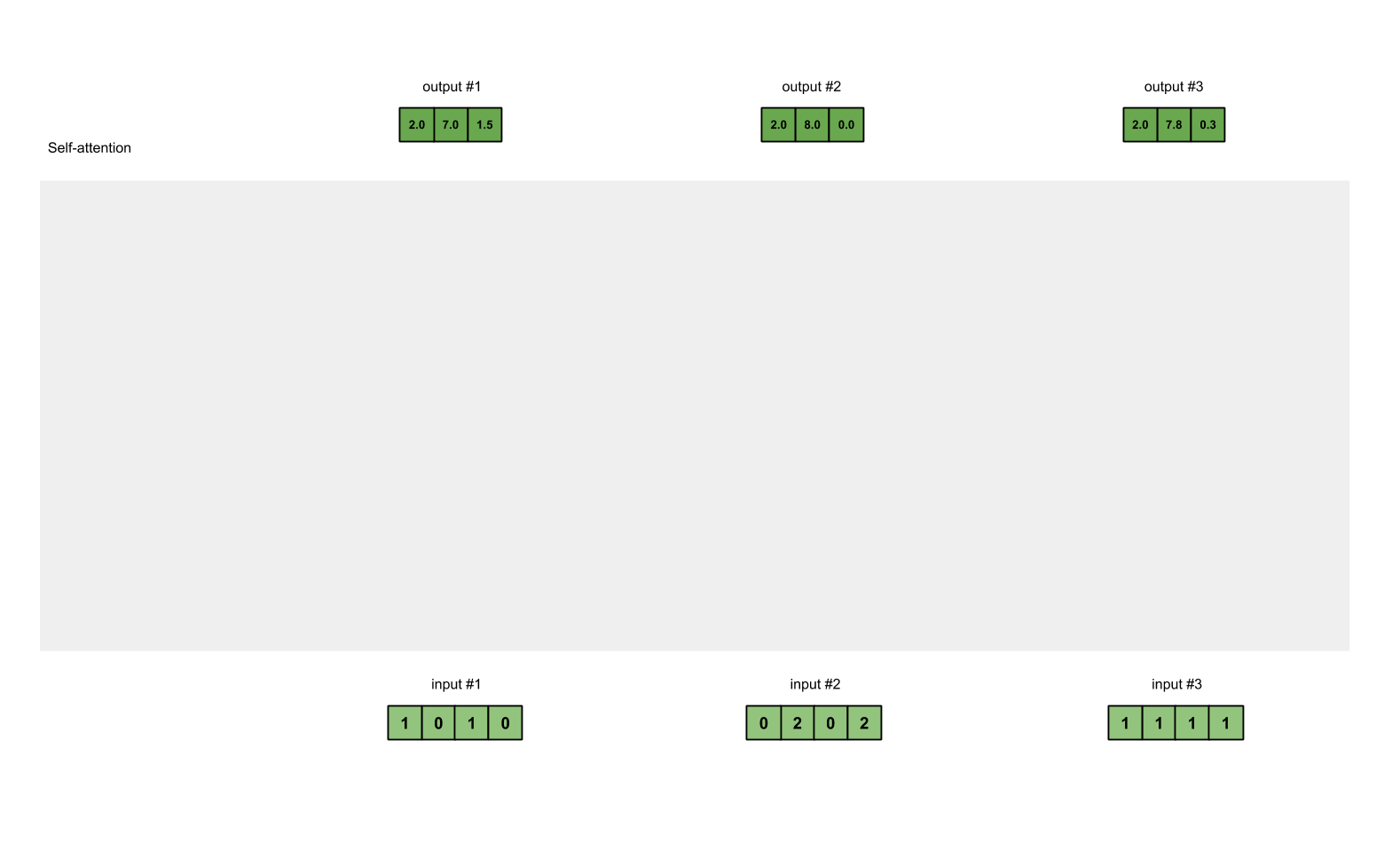
第八步：对输入2、3，重复第4-7步

既然我们已经完成了输入1，我们重复步骤4-7能得到输出2和3。这个可以留给读者自己尝试，相信聪明的你可以做出来。

代码

这里有PyTorch的实现代码，PyTorch是一个主流的Python深度学习框架。为了能够很好地使用代码片段中的@运算符, .T and None操作，请确保Python≥3.6，PyTorch ≥1.3.1。

1. 准备输入

import torch

x = [

  [1, 0, 1, 0], # Input 1

  [0, 2, 0, 2], # Input 2

  [1, 1, 1, 1]  # Input 3

 ]

x = torch.tensor(x, dtype=torch.float32)

2. 初始化权重

w_key = [

  [0, 0, 1],

  [1, 1, 0],

  [0, 1, 0],

  [1, 1, 0]

]

w_query = [

  [1, 0, 1],

  [1, 0, 0],

  [0, 0, 1],

  [0, 1, 1]

]

w_value = [

  [0, 2, 0],

  [0, 3, 0],

  [1, 0, 3],

  [1, 1, 0]

]

w_key = torch.tensor(w_key, dtype=torch.float32)

w_query = torch.tensor(w_query, dtype=torch.float32)

w_value = torch.tensor(w_value, dtype=torch.float32)

3. 获取`key`，`query`和`value`



keys = x @ w_key

querys = x @ w_query

values = x @ w_value

print(keys)

# tensor([[0., 1., 1.],

#         [4., 4., 0.],

#         [2., 3., 1.]])

print(querys)

# tensor([[1., 0., 2.],

#         [2., 2., 2.],

#         [2., 1., 3.]])

print(values)

# tensor([[1., 2., 3.],

#         [2., 8., 0.],

#         [2., 6., 3.]])

4. 为第1个输入计算注意力分数

attn_scores = querys @ keys.T

# tensor([[ 2.,  4.,  4.],  # attention scores from Query 1

#         [ 4., 16., 12.],  # attention scores from Query 2

#         [ 4., 12., 10.]]) # attention scores from Query 3

5. 计算softmax

from torch.nn.functional import softmax

attn_scores_softmax = softmax(attn_scores, dim=-1)

# tensor([[6.3379e-02, 4.6831e-01, 4.6831e-01],

#         [6.0337e-06, 9.8201e-01, 1.7986e-02],

#         [2.9539e-04, 8.8054e-01, 1.1917e-01]])

# For readability, approximate the above as follows

attn_scores_softmax = [

  [0.0, 0.5, 0.5],

  [0.0, 1.0, 0.0],

  [0.0, 0.9, 0.1]

]

attn_scores_softmax = torch.tensor(attn_scores_softmax)

6. 将分数乘以values

weighted_values = values[:,None] * attn_scores_softmax.T[:,:,None]

# tensor([[[0.0000, 0.0000, 0.0000],

#          [0.0000, 0.0000, 0.0000],

#          [0.0000, 0.0000, 0.0000]],

#

#         [[1.0000, 4.0000, 0.0000],

#          [2.0000, 8.0000, 0.0000],

#          [1.8000, 7.2000, 0.0000]],

#

#         [[1.0000, 3.0000, 1.5000],

#          [0.0000, 0.0000, 0.0000],

#          [0.2000, 0.6000, 0.3000]]])

7. 对权重化后的values求和，得到输出

outputs = weighted_values.sum(dim=0)

# tensor([[2.0000, 7.0000, 1.5000],  # Output 1

#         [2.0000, 8.0000, 0.0000],  # Output 2

#         [2.0000, 7.8000, 0.3000]]) # Output 3

注意：PyTorch已经提供了这个API，名字为nn.MultiheadAttention。但是，这个API需要你提供PyTorch的Tensor形式的key，value，query。还有，这个模块的输出会经历一个线性变换。

自己实现？

以下是笔者自己写的部分。

对于不熟悉PyTorch的读者来说，上述的向量操作理解起来有点困难，因此，笔者自己用简单的Python代码实现了一遍上述Self-Attention的过程。

完整的Python代码如下：

# -*- coding: utf-8 -*-

from typing import List

import math

from pprint import pprint

x = [[1, 0, 1, 0], # Input 1

     [0, 2, 0, 2], # Input 2

     [1, 1, 1, 1]  # Input 3

    ]

w_key = [[0, 0, 1],

        [1, 1, 0],

        [0, 1, 0],

        [1, 1, 0]

        ]

w_query = [[1, 0, 1],

            [1, 0, 0],

            [0, 0, 1],

            [0, 1, 1]

          ]

w_value = [[0, 2, 0],

            [0, 3, 0],

            [1, 0, 3],

            [1, 1, 0]

          ]

# vector dot of two vectors

def vector_dot(list1: List[float or int], list2: List[float or int]) -> float or int:

    dot_sum = 0

    for element_i, element_j in zip(list1, list2):

        dot_sum += element_i * element_j

    return dot_sum

# get weights matrix by x, using matrix multiplication

def get_weights_matrix_by_x(x, weight_matrix):

    x_matrix = []

    for i in range(len(x)):

        x_row = []

        for j in range(len(weight_matrix[0])):

            x_row.append(vector_dot(x[i], [_[j] for _ in weight_matrix]))

        x_matrix.append(x_row)

    return x_matrix

# softmax function

def softmax(x: List[float or int]) -> List[float or int]:

    x_sum = sum([math.exp(_) for _ in x])

    return [math.exp(_)/x_sum for _ in x]

x_key = get_weights_matrix_by_x(x, w_key)

x_value = get_weights_matrix_by_x(x, w_value)

x_query = get_weights_matrix_by_x(x, w_query)

# print(x_key)

# print(x_value)

# print(x_query)

outputs = []

for query in x_query:

    score_list = [vector_dot(query, key) for key in x_key]

    softmax_score_list = softmax(score_list)

    weights_list = []

    for i in range(len(softmax_score_list)):

        weights = [softmax_score_list[i] * _ for _ in x_value[i]]

        weights_list.append(weights)

    output = []

    for j in range(len(weights_list[0])):

        output.append(sum([_[j] for _ in weights_list]))

    outputs.append(output)

pprint(outputs)

输出结果如下：

[[1.9366210616669624, 6.683105308334811, 1.5950684074995565],

 [1.9999939663351456, 7.9639915951322156, 0.0539764053125496],

 [1.9997046127769653, 7.759892254657784, 0.3583892946751152]]

总结

本文主要讲述了如何一步一步来实现Self-Attention机制，对于想要自己实现算法的读者来说，值得一读。

本文分享到此结束，感谢大家的阅读~