ODEINT 求解常微分方程（2）

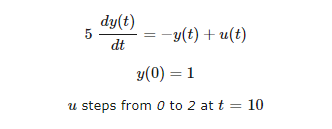
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dy/dt
def model(y,t):
    # u steps from 0 to 2 at t=10
    if t<10.0:
        u = 0
    else:
        u = 2
    dydt = (-y + u)/5.0
    return dydt

# initial condition
y0 = 1

# time points
t = np.linspace(0,40,1000)

# solve ODE
y = odeint(model,y0,t)

# plot results
plt.plot(t,y,'r-',label='Output (y(t))')
plt.plot([0,10,10,40],[0,0,2,2],'b-',label='Input (u(t))')
plt.ylabel('values')
plt.xlabel('time')
plt.legend(loc='best')
plt.show()