最长公共子序列/子串 LCS（模板）

首先区分子序列和子串，序列不要求连续性（连续和不连续都可以），但子串一定是连续的

1.最长公共子序列

1、最长公共子序列问题有最优子结构，这个问题可以分解称为更小的问题

2、同时，子问题的解释可以被重复使用的，也就是说更高级别的子问题会重用更小子问题的解。

满足这两点以后，很容易就想到用动态规划来求解。

1.假设两个字符串s1, s2。当其中一个串的长度为0时，公共子序列的长度肯定为0。

2.假设s1的第i个字符与s2的第j个字符相等时，最长子序列等于s1的第i-1个字符与s2的第j-1个字符最长子序列长度+1。

3.假设s1的第i个字符与s2的第j个字符不相等时，最长子序列等于s1的第i个字符与s2的第j-1个字符最长子序列长度或s1的第i-1个字符与s2的第j个字符最

长子序列长度中最大那一个。

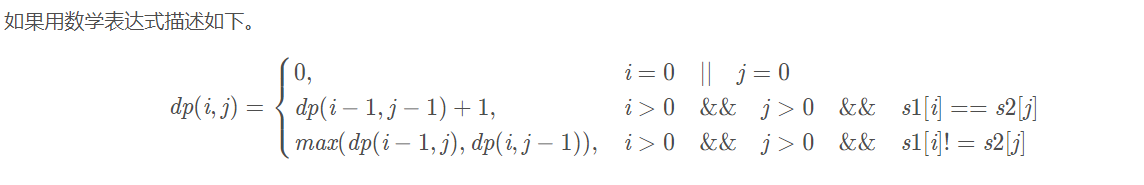
dp[i][j]表示s1的第i个字符与s2的第j-1个字符最长子序列长度

​

#include<iostream>
#include<math.h>
#include<string.h>
using namespace std;
int dp[][];
int len1,len2;
void lcs(string s1,string s2)
{
    for(int i=;i<=len1;i++)//初始化
        dp[i][]=;
    for(int i=;i<=len2;i++)
        dp[][i]=;
    for(int i=;i<=len1;i++)
    {
        for(int j=;j<=len2;j++)
        {
            if(s1[i-]==s2[j-])
                dp[i][j]=dp[i-][j-]+;
            else
                dp[i][j]=max(dp[i-][j],dp[i][j-]);
        }
    }

}
void Print(string s1,string s2)//输出公共子序列
{
    string str="";
    while(len1>=&&len2>=)//从字符串s1,s2的末尾位置往前推
    {
        if(s1[len1-]==s2[len2-])
        {
            str=str+s1[len1-];
            len1--;
            len2--;
        }
        else
        {
            if(dp[len1][len2-]>dp[len1-][len2])//说明公共的字符在字符串s1的i位置之前，与字符s2[j]无关
                len2--;
            else
                len1--;
        }
    }
    for(int i=str.length();i>=;i--)
        cout<<str[i]<<' ';
    cout<<endl;
}
int main()
{
    string s1,s2;
    cin>>s1>>s2;
    len1=s1.length();
    len2=s2.length();
    lcs(s1,s2);
    cout<<dp[len1][len2]<<endl;
    Print(s1,s2);
    return ;
}

// aaeefdhe
// saabcd

//3
// a a d

​

2.最长公共子串

最长公共子串跟最长公共子序列的唯一区别在于，公共子串要求是连续的，子序列要求不一定连续。

具体的思路还是动态规划，不同点在于动态规划的迭代策略

#include<iostream>
#include<math.h>
#include<string.h>
using namespace std;
int dp[][];
int len1,len2;
int mx_len=,End=;//End是公共字串结束的位置
void lcs(string s1,string s2)
{
    for(int i=;i<=len1;i++)//初始化
        dp[i][]=;
    for(int i=;i<=len2;i++)
        dp[][i]=;
    for(int i=;i<=len1;i++)
    {
        for(int j=;j<=len2;j++)
        {
            if(s1[i-]==s2[j-])
                dp[i][j]=dp[i-][j-]+;
            else
                dp[i][j]=;

            if(dp[i][j]>mx_len)
            {
                mx_len=dp[i][j];
                End=i-;
            }
        }
    }

}

int main()
{
    string s1,s2;
    cin>>s1>>s2;
    len1=s1.length();
    len2=s2.length();
    lcs(s1,s2);
    cout<<mx_len<<endl;
    for(int i=End-mx_len+;i<=End;i++)
        cout<<s1[i];
    cout<<endl;
    return ;
}

// aaeefdhe
// saabcd

//2
//aa