GBDT梯度提升树算法及官方案例

梯度提升树是一种决策树的集成算法。它通过反复迭代训练决策树来最小化损失函数。决策树类似，梯度提升树具有可处理类别特征、易扩展到多分类问题、不需特征缩放等性质。Spark.ml通过使用现有decision tree工具来实现。

梯度提升树依次迭代训练一系列的决策树。在一次迭代中，算法使用现有的集成来对每个训练实例的类别进行预测，然后将预测结果与真实的标签值进行比较。通过重新标记，来赋予预测结果不好的实例更高的权重。所以，在下次迭代中，决策树会对先前的错误进行修正。

对实例标签进行重新标记的机制由损失函数来指定。每次迭代过程中，梯度迭代树在训练数据上进一步减少损失函数的值。spark.ml为分类问题提供一种损失函数（Log Loss），为回归问题提供两种损失函数（平方误差与绝对误差）。

Spark.ml支持二分类以及回归的随机森林算法，适用于连续特征以及类别特征。不支持多分类问题。

# -*- coding: utf-8 -*-
"""
Created on Wed May  9 09:53:30 2018

@author: admin
"""

import numpy as np
import matplotlib.pyplot as plt

from sklearn import ensemble
from sklearn import datasets
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error

# #############################################################################
# Load data
boston = datasets.load_boston()
X, y = shuffle(boston.data, boston.target, random_state=13)
X = X.astype(np.float32)
offset = int(X.shape[0] * 0.9)
X_train, y_train = X[:offset], y[:offset]
X_test, y_test = X[offset:], y[offset:]

# #############################################################################
# Fit regression model
params = {'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 2,
          'learning_rate': 0.01, 'loss': 'ls'}   #随便指定参数长度，也不用在传参的时候去特意定义一个数组传参
clf = ensemble.GradientBoostingRegressor(**params)

clf.fit(X_train, y_train)
mse = mean_squared_error(y_test, clf.predict(X_test))
print("MSE: %.4f" % mse)

# #############################################################################
# Plot training deviance

# compute test set deviance
test_score = np.zeros((params['n_estimators'],), dtype=np.float64)

for i, y_pred in enumerate(clf.staged_predict(X_test)):
    test_score[i] = clf.loss_(y_test, y_pred)

plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.title('Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, clf.train_score_, 'b-',
         label='Training Set Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, test_score, 'r-',
         label='Test Set Deviance')
plt.legend(loc='upper right')
plt.xlabel('Boosting Iterations')
plt.ylabel('Deviance')

# #############################################################################
# Plot feature importance
feature_importance = clf.feature_importances_
# make importances relative to max importance
feature_importance = 100.0 * (feature_importance / feature_importance.max())
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
plt.subplot(1, 2, 2)
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, boston.feature_names[sorted_idx])
plt.xlabel('Relative Importance')
plt.title('Variable Importance')
plt.show()

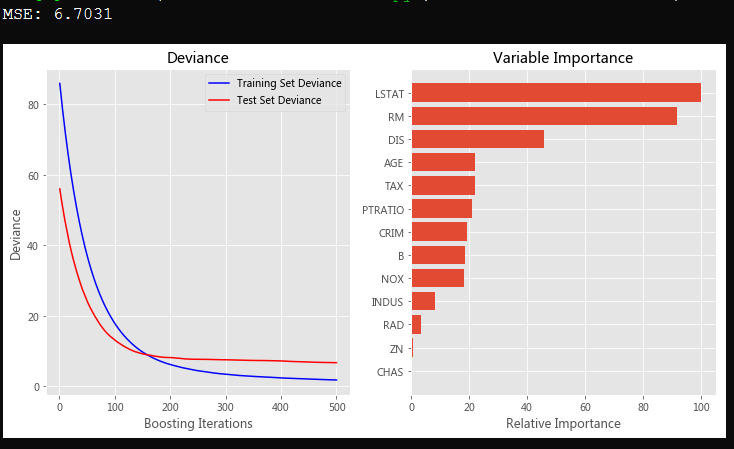
房产数据介绍：

- CRIM     per capita crime rate by town 
- ZN       proportion of residential land zoned for lots over 25,000 sq.ft. 
- INDUS    proportion of non-retail business acres per town 
- CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) 
- NOX      nitric oxides concentration (parts per 10 million) 
- RM       average number of rooms per dwelling 
- AGE      proportion of owner-occupied units built prior to 1940 
- DIS      weighted distances to five Boston employment centres 
- RAD      index of accessibility to radial highways 
- TAX      full-value property-tax rate per $10,000 
- PTRATIO  pupil-teacher ratio by town 
- B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town 
- LSTAT    % lower status of the population 
- MEDV     Median value of owner-occupied homes in $1000'

参考：http://scikit-learn.org/stable/auto_examples/ensemble/plot_gradient_boosting_regression.html#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regression-py