（原创）不过如此的 DFS 深度优先遍历

DFS 深度优先遍历

DFS算法用于遍历图结构，旨在遍历每一个结点，顾名思义，这种方法把遍历的重点放在深度上，什么意思呢？就是在访问过的结点做标记的前提下，一条路走到天黑，我们都知道当每一个结点都有很多分支，那么我们的小人就沿着每一个结点走，定一个标准，比如优先走右手边的路，然后在到达下一个结点前先敲敲门，当一个结点的所有门都被敲了个遍都标记过，那么就走回头路，再重复敲门，直到返回起点，这样的方式我们叫做 DFS 深度优先遍历，本文以图结构讲解，例子取自《大话数据结构》。

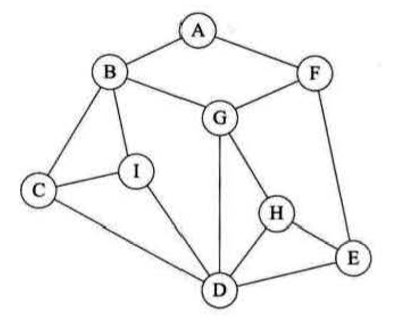
如我刚才所讲，从A点出发，将路径画出来就是以下效果。

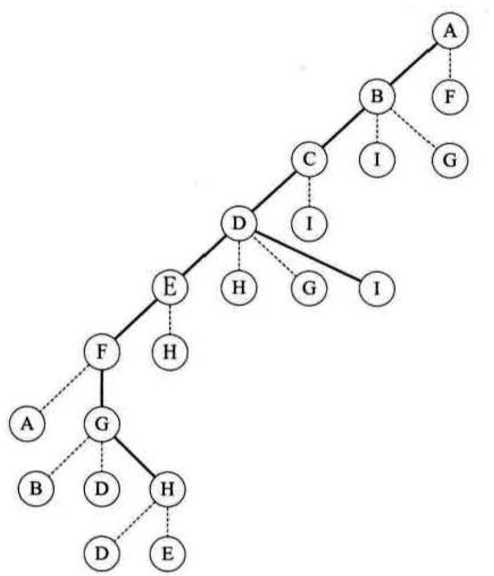
实线是走过的路程，虚线就是我们的小人敲门然后发现标记过的一个过程，大家可以寄几模拟一哈。一句话总结就是：

从图中某个顶点 v 出发，访问此顶点，然后从 v 的未被访问的邻接点出发 深度优先遍历图结构，直至图中所有和 v 有路径相通的顶点都被访问到。

结构定义代码：

typedef char VertexType;
typedef int EdgeType;

#define MAXVEX 10
#define INFINITY 65535

typedef int boolean;
boolean visited[MAXVEX];

typedef struct
{
    VertexType vexs[MAXVEX];
    EdgeType arc[MAXVEX][MAXVEX];
    int numVertexes,numEdges;
}MGraph;

邻接矩阵创建：

void CreateMGraph(MGraph *G)
{
    int i,j,k;
    printf("请输入顶点数和边数（空格隔开）\n");
    scanf("%d %d",&G->numVertexes,&G->numEdges);
    printf("请依次输入每个顶点的内容：\n");
    for(i = ;i < G->numVertexes;i++)
    {
        scanf("%c",&G->vexs[i]);
    }
    for(i = ;i < G->numVertexes;i++)
    {
        for(j = ;j < G->numVertexes;j++)
        {
            G->arc[i][j] = INFINITY;
        }
    }
    for(k = ;k < G->numEdges;k++)
    {
        printf("输入边（vi,vj）上的下标i，下标j：\n");
        scanf("%d %d",&i,&j);
        G->arc[i][j] = ;
        G->arc[j][i] = G->arc[i][j];
    }
}

DFS算法

void DFS(MGraph G,int i) //深度优先递归算法
{
    int j;
    visited[i] = ;
    printf("%c",G.vexs[i]);
    for(j = ;j < G.numVertexes;j++)
    {
        if(G.arc[i][j] ==  && !visited[j])
            DFS(G,j);
    }
}
void DFStraverse(MGraph G)  //深度遍历
{
    int i;
    for(i = ;i < G.numVertexes;i++)
    visited[i] = ;
    for(i = ;i < G.numVertexes;i++)
    {
        if(!visited[i])
            DFS(G,i);
    }
}

这种方法比较好理解在于使用循环进入函数再递归，可以保证以邻接矩阵为储存单位的每一个格子都被遍历到，且做好标注，那么用邻接矩阵的DFS算法时间复杂度可以想见是 O（n²），嵌套两重循环，

我们来看下一种实现方式，这次我们使用的是邻接单链表

结构定义：

typedef int boolean;
boolean visited[MAXVEX];

typedef char VertexType;
typedef int EdgeType;

#define MAXVEX 10
#define INFINITY 65535

typedef struct EdgeNode //边表结构点
{
    int adjvex;
    struct EdgeNode *next;
}EdgeNode;

typedef struct VertexNode //顶点表结构点
{
    VertexType data;
    EdgeNode *firstedge;
}VertexNode,AdjList[MAXVEX];

typedef struct //总表结构
{
    AdjList adjList;
    int numVertexes,numEdges;
}GraphAdjList;

比邻接矩阵复杂一点，但是其结构只有三种，总表、定点表和边表

创建：

void CreateALGraph(GraphAdjList *G)
{
    int i,j,k;
    EdgeNode *e;
    printf("请输入顶点数和边数（空格隔开）\n");
    scanf("%d %d",&G->numVertexes,&G->numEdges);
    for(i = ;i < G->numVertexes;i++)
    {
        scanf("%c",&G->adjList[i].data);
        G->adjList[i].firstedge = NULL;
    }
    for(k = ;k < G->numVertexes;k++)
    {
        printf("输入边（vi,vj）上的下标i，下标j：\n");
        scanf("%d %d",&i,&j);
        e = (EdgeNode*)malloc(sizeof(EdgeNode));
        e->adjvex=i;
        e->next = adjList[j].firstedge;
        adjList[j].firstedge = e;

        e = (EdgeNode*)malloc(sizeof(EdgeNode));
        e->adjvex=j;
        e->next = adjList[i].firstedge;
        adjList[i].firstedge = e;
    }
}

DFS算法实现：

void DFS(GraphAdjList GL,int i)
{
    EdgeNode *p;
    visited[i] = ;
    printf("%c",GL->adjList[i].data);
    while(p)
    {
        if(!visited[p->adjvex])
            DFS(GL,p->adjvex);
        p = p->next;
    }
}

void DFStraverse(GraphAdjList GL)
{
    int i;
    for(i = ;i < GL->numVertexes;i++)
    visited[i] = ;
    for(i = ;i < GL->numVertexes;i++)
    {
        if(!visited[i])
            DFS(GL,i);
    }
}

利用邻接表的方式能够实现相同效果的遍历，同时这种方法的算法时间复杂度为 O（n+e）

显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。