题解：P4586 [FJOI2015] 最小覆盖双圆问题

写了这么久终于过了，发篇题解记录一下。

第一次写黑题题解，写的不好请见谅。

目录

1. 本题思路
2. 三点定圆
3. 最小圆覆盖
4. 关于最小圆覆盖时间复杂度
5. 回到本题
6. 二分法划分点集
7. 总时间复杂度
8. 最小覆盖双圆问题代码

本题思路

首先，这道题叫做最小覆盖双圆问题，这道题涉及到一个叫做最小圆覆盖的问题。

一个容易想到的思路：若我们能做出最小圆覆盖的问题，就可以把本题分成两个圆，也就是两个点集来处理。

那我们如何处理最小圆覆盖的问题呢？

三点定圆

首先，不共线的三个点可以确定一个圆。

作任意两点所在线段的中垂线，三条中垂线的交点就是这三个点共圆的圆心。这个圆心到三点中的任意一点就是这个圆的半径。当三点不在同一条直线时。形成一个三角形，而三角形有且只有一个外接圆。

数学原理是中垂线上的点到线段两端的距离相等。两条中垂线的交点，到两条线段的距离都相等。所以，不在同一条直线的三点可以确定一个圆。

附三角形的外切圆半径公式：\(\frac{abc}{4S}\)，其中，\(S\) 表示三角形的面积，\(a\) 和 \(b\) 和 \(c\) 分别为三角形的三条边。

本部分代码：

Point circle_center(const Point a,const Point b,const Point c){
	Point center;
	double a1=b.x-a.x,b1=b.y-a.y,c1=(a1*a1+b1*b1)/2;
	double a2=c.x-a.x,b2=c.y-a.y,c2=(a2*a2+b2*b2)/2;
	double d=a1*b2-a2*b1;
	center.x=a.x+(c1*b2-c2*b1)/d;
	center.y=a.y+(a1*c2-a2*c1)/d;
	return center;
}

最小圆覆盖

根据以上结论，我们知道对于任意三个不共线的点，我们可以求出三点定圆，所以一个明显的想法就是枚举三个点。

具体步骤如下：

1. 枚举第一个点 \(i\)，若不在目前圆内，设它为圆心。

2. 枚举第二个点 \(j\)，若不在当前圆内，设当前圆为以 \(i\) 和 \(j\) 为直径的圆。

3. 枚举第三个点 \(k\)，若不在当前圆内，设当前圆为 \(i\) 和 \(j\) 和 \(k\) 的外接圆。

显然最优解一定是两个点为直径的圆或者一个三角形的外接圆，否则肯定能缩的更小。这样做就是正确的。

这就是所谓的增量法。

关于最小圆覆盖时间复杂度

显然，按上面的做法，时间复杂度是 \(O(n^3)\) 的，会被不良心的出题人卡掉。

所以，我们需要打乱数据，从而提升时间复杂度。

这就是所谓的随机增量法。

时间复杂度期望 \(O(n)\)。

最小圆覆盖代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define eps 1e-8
const int N=1e5+1;
int sgn(double x){
	if(fabs(x)<eps) return 0;
	else return x<0?-1:1;
}
struct Point{double x,y;};
double Distance(Point A,Point B){return hypot(A.x-B.x,A.y-B.y);};
Point circle_center(const Point a,const Point b,const Point c){
	Point center;
	double a1=b.x-a.x,b1=b.y-a.y,c1=(a1*a1+b1*b1)/2;
	double a2=c.x-a.x,b2=c.y-a.y,c2=(a2*a2+b2*b2)/2;
	double d=a1*b2-a2*b1;
	center.x=a.x+(c1*b2-c2*b1)/d;
	center.y=a.y+(a1*c2-a2*c1)/d;
	return center;
}
void min_cover_circle(Point *p,int n,Point &c,double &r){
	random_shuffle(p,p+n);
	c=p[0],r=0;
	for(int i=1;i<n;i++){
		if(sgn(Distance(p[i],c)-r)>0){
			c=p[i];r=0;
			for(int j=0;j<i;j++){
				if(sgn(Distance(p[j],c)-r)>0){
					c.x=(p[i].x+p[j].x)/2;
					c.y=(p[i].y+p[j].y)/2;
					r=Distance(p[j],c);
					for(int k=0;k<j;k++){
						if(sgn(Distance(p[k],c)-r)>0){
							c=circle_center(p[i],p[j],p[k]);
							r=Distance(p[i],c);
						}
					}
				}
			}
		}
	}
}
Point p[N];
signed main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++) cin>>p[i].x>>p[i].y;
    Point c;double r;
    min_cover_circle(p,n,c,r);
    printf("%.10f\n%.10f %.10f\n",r,c.x,c.y);
    return 0;
}

最小圆覆盖例题：这里。

回到本题

之前说若我们能做出最小圆覆盖的问题，就可以把本题分成两个圆，也就是两个点集来处理。

现在我们已经会了最小圆覆盖的问题，如何划分点集呢？

如果暴力枚举，显然不行。

这时引出我们的二分法。

二分法划分点集

用二分求出一条与 \(X\) 轴垂直的直线，然后再求解。

如果正解是斜着画一条直线呢？

这时，我们旋转坐标系！

每次旋转之后都求一次最小双圆覆盖，然后再取最优值即是答案。如何对每个点进行“旋转”?

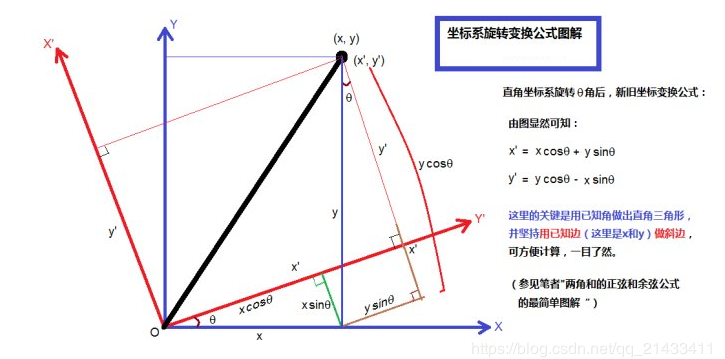
可以看图来理解。

坐标系旋转 \(180\) 度就是原坐标系了，所以只要转 \(180\) 度就好了。

总时间复杂度

首先，要转 \(180\) 次，每次中要二分直线，再做最小圆覆盖。

总时间复杂度 \(O(n \log n)\)。

最小覆盖双圆问题代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define eps 1e-8
int n;
const int N=1e5+1;
struct Point{double x,y;};
Point p[N],a[N];
double Distance(Point A,Point B){return hypot(A.x-B.x,A.y-B.y);};
int cmp(Point a, Point b){return a.x<b.x;}
int sgn(double x){
	if(fabs(x)<eps) return 0;
	else return x<0?-1:1;
}
Point rotate(const Point &b) {
	Point t;
    t.x=b.x*cos(1.0/180*acos(-1))+b.y*sin(1.0/180*acos(-1));
    t.y=b.y*cos(1.0/180*acos(-1))-b.x*sin(1.0/180*acos(-1));
    return t;
}
Point circle_center(const Point a,const Point b,const Point c){
	Point center;
	double a1=b.x-a.x,b1=b.y-a.y,c1=(a1*a1+b1*b1)/2;
	double a2=c.x-a.x,b2=c.y-a.y,c2=(a2*a2+b2*b2)/2;
	double d=a1*b2-a2*b1;
	center.x=a.x+(c1*b2-c2*b1)/d;
	center.y=a.y+(a1*c2-a2*c1)/d;
	return center;
}
double min_cover_circle(int n1,int n2){
	if(n1>n2) return 0;
	for(int i=n1;i<=n2;i++) a[i]=p[i];
	random_shuffle(a+n1+1,a+n2+1);
	Point c=a[n1];
	double r=0;
	for(int i=n1;i<=n2;i++){
		if(sgn(Distance(a[i],c)-r)>0){
			c=a[i];r=0;
			for(int j=n1;j<i;j++){
				if(sgn(Distance(a[j],c)-r)>0){
					c.x=(a[i].x+a[j].x)/2;
					c.y=(a[i].y+a[j].y)/2;
					r=Distance(a[j],c);
					for(int k=n1;k<=j;k++){
						if(sgn(Distance(a[k],c)-r)>0){
							c=circle_center(a[i],a[j],a[k]);
							r=Distance(a[i],c);
						}
					}
				}
			}
		}
	}
	return r;
}
void init(int n){
	double R=1e9;
    for(int i=1;i<=n;i++) cin>>p[i].x>>p[i].y;
    for(int i=1;i<=180;i++){
        for(int i=1;i<=n;i++) p[i]=rotate(p[i]);
        sort(p+1,p+n+1,cmp);
        int l=1,r=n;
        while(l<=r) {
            int mid=(l+r)/2;
            double R1=min_cover_circle(1,mid),R2=min_cover_circle(mid+1,n);
            if(min(R1,R2)>R) break;
            if(R1<R2)l=mid+1;
            else r=mid-1;
            R=min(R,max(R1, R2));
        }
    }
    printf("%.2f\n",R);
}
signed main(){
    while(cin>>n&&n!=0){init(n);}
    return 0;
}

如果本篇题解还可以，就点个赞吧！