[题目] Luogu P1312 Mayan游戏

题面

题目描述
$ Mayan puzzle $是最近流行起来的一个游戏。游戏界面是一个 \(7行 \times 5列\)的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1 、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图\(6\)到图\(7\)）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图1 和图2）；

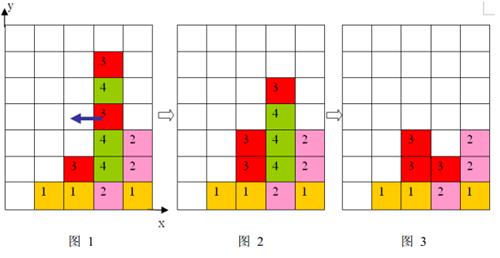
2 、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1 到图3）。

注意：

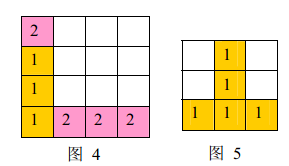
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图\(4\)，三个颜色为\(1\)的方块和三个颜色为$2 $的方块会同时被消除，最后剩下一个颜色为\(2\)的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5 所示的情形，5 个方块会同时被消除）。

3 、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0 ），将位于（3, 3 ）的方块向左移动之后，游戏界面从图 1 变成图 2 所示的状态，此时在一竖列上有连续三块颜色为4 的方块，满足消除条件，消除连续3 块颜色为4 的方块后，上方的颜色为3 的方块掉落，形成图 3 所示的局面。

输入输出格式
输入格式：
共 6 行。

第一行为一个正整数\(n\)，表示要求游戏通关的步数。

接下来的\(5\)行，描述$ 7 \times 5$的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个$0 $结束，自下向上表示每竖列方块的颜色编号（颜色不多于\(10\)种，从\(1\)开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式：
如果有解决方案，输出\(n\)行，每行包含\(3\)个整数\(x,y,g\)，表示一次移动，每两个整数之间用一个空格隔开，其中\((x,y)\)表示要移动的方块的坐标，\(g\)表示移动的方向，\(1\)表示向右移动，\(−1\)表示向左移动。注意：多组解时，按照xx为第一关健字，\(y\)为第二关健字，\(1\)优先于\(−1\)，给出一组字典序最小的解。游戏界面左下角的坐标为\((0,0)\)。

如果没有解决方案，输出一行，包含一个整数\(-1\)。

输入输出样例
输入样例#1：
3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0
输出样例#1：
2 1 1
3 1 1
3 0 1

说明
【输入输出样例说明】
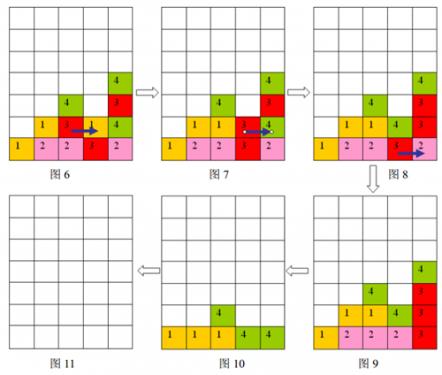
按箭头方向的顺序分别为图\(6\)到图\(11\)
样例输入的游戏局面如上面第一个图片所示，依次移动的三步是：\((2,1)\)处的方格向右移动，\((3,1)\)处的方格向右移动，\((3,0)\)处的方格向右移动，最后可以将棋盘上所有方块消除。

【数据范围】
对于\(30%\)的数据，初始棋盘上的方块都在棋盘的最下面一行；
对于\(100%\)的数据，\(0<n≤5\) 。

思路

觉得这道题写得挺有意思的，思路有空再补吧233，代码也没注释……

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#define re register
using namespace std;
//全局变量
int n;//步数
int step[10][10][10];//dfs状态回溯
struct result_ans {
    int x,y,way;
}ans[10];//答案存储
// Mayan游戏实现部分
struct Mayan_puzzle {
    int a[10][10];//color <=10
    int ax[105],ay[105],T;
    inline bool go() {    //游戏进行-判断是否可以消除并消除
        T=0;    int flag=0;
        for(re int i=0;i<=2;i++)
            for(re int j=0;j<=6;j++) if(a[i][j]) {
            if(a[i][j]==a[i+1][j]&&a[i+1][j]==a[i+2][j]) {
                flag = 1; ax[++T] = i; ay[T] = j;
                ax[++T]=i+1; ay[T]=j; ax[++T]=i+2; ay[T]=j;
            }
        }
        for(re int i=0;i<=4;i++)
            for(re int j=0;j<=4;j++) if(a[i][j]) {
            if(a[i][j]==a[i][j+1]&&a[i][j+1]==a[i][j+2]) {
                flag = 1; ax[++T] = i; ay[T] = j;
                ax[++T]=i; ay[T]=j+1; ax[++T]=i; ay[T]=j+2;
            }
        }
        for(re int i=1;i<=T;i++) a[ax[i]][ay[i]]=0;
        return flag;
    }
    inline void down() {    //下降处理-悬空方块下落
        for(re int i=0;i<=4;i++)
            for(re int j=1;j<=6;j++) if(a[i][j])    {
            int k=j;
            while(a[i][k-1]==0) {
                swap(a[i][k-1],a[i][k]);
                if(k==1) break; else k--;
            }
        }
    }
    inline bool check() {   //结束判断-判断是否全部消除
        for(re int i=0;i<=4;i++)
            if(a[i][0]) return false;
        return true;
    }
};
struct Mayan_puzzle p;
// in / out 输入输出
inline void getin() {
    int color=0,T;  scanf("%d",&n);
    for(re int i=0;i<=4;i++) {  T=-1;
        while(scanf("%d",&color)&&color) p.a[i][++T]=color;
    }
}
inline void print() {
    for(re int i=1;i<=n;i++)
        printf("%d %d %d\n",ans[i].x,ans[i].y,ans[i].way);
}
// dfs 搜索部分
void dfs(int cur) {
    if(cur>n) {
        if(p.check()) {
            print();//out
            exit(0);//退出程序
        }
        return;
    }
    for(re int i=0;i<=4;i++)
        for(re int j=0;j<=6;j++)
    {
        if(p.a[i][j]&&i<=3) {   //right
            for(re int k=0;k<=4;k++)
                for(re int l=0;l<=6;l++)
                    step[cur][k][l] = p.a[k][l];
            swap( p.a[i][j] , p.a[i+1][j] );
            ans[cur].x =i; ans[cur].y =j; ans[cur].way =1;
            p.down();
            while( p.go())  p.down();
            dfs(cur+1);
            for(re int k=0;k<=4;k++)
                for(re int l=0;l<=6;l++)
                    p.a[k][l] = step[cur][k][l];
        }
        if(p.a[i][j]&&p.a[i-1][j]==0&&i>=1) {   //left
            for(re int k=0;k<=4;k++)
                for(re int l=0;l<=6;l++)
                    step[cur][k][l] = p.a[k][l];
            swap( p.a[i][j] , p.a[i-1][j] );
            ans[cur].x =i; ans[cur].y =j; ans[cur].way =-1;
            p.down();
            while( p.go())  p.down();
            dfs(cur+1);
            for(re int k=0;k<=4;k++)
                for(re int l=0;l<=6;l++)
                    p.a[k][l] = step[cur][k][l];
        }
    }
}
//main函数
int main() {
    getin();//in
    dfs(1);//dfs
    printf("-1\n");//无解时输出-1
    return 0;
}