luogu P2742 【模板】二维凸包

嘟嘟嘟




没错，我开始学凸包了。

其实挺简单的。




前置技能：

1.极坐标系

2.向量叉积




1.极坐标系

就是一种二维坐标系。只不过两个坐标分别表示向量和极轴的角度和自身的长度。对于不同的问题，极轴可以自己选取。

2.向量叉积

不说了




算法是\(Graham\)扫描法，下面讲一下实现步骤：

1.在所有点中找到横坐标最小的点作为极点，如果有多个，取纵坐标最小的点。

2.对于其他\(n -1\)个点进行极角排序，极角相同比较到极点距离。

排完序后的图大概是这个样子的：



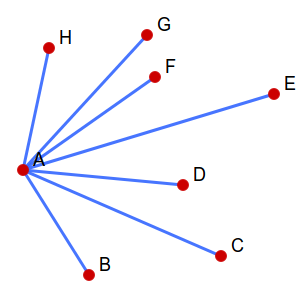
其中的字母就是排完序后的序号。

3.然后维护一个栈，对于每一个点，比较他和栈顶的两个点构成的线段，如果在线段的右边，就把栈顶弹出，直到栈中只剩一个元素或该点在线段右边为止。

4.最后栈中的元素就是凸包的顶点。




再补充几点：

1.极角排序的函数怎么写。

对于极点\(A\)和要排序的两个点\(B, C\)。就是看\(C\)在\(AB\)的上方还是下方。这个用叉积判断即可。如果\(\overrightarrow{AB} \times \overrightarrow{AC} < 0\)，说明\(C\)在\(AB\)下方，反之亦然。

如果叉积等于\(0\)，比较到\(A\)点距离。

2.判断点\(i\)在栈顶两个元素所成直线的左右。

跟上面一样，叉积。

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
#define enter puts("")
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define rg register
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 1e4 + 5;
inline ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
inline void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}

int n;
struct Vec
{
  db x, y;
  db operator * (const Vec& oth)const
  {
    return x * oth.y - oth.x * y;
  }
  friend inline db dis(const Vec& A)
  {
    return A.x * A.x + A.y * A.y;
  }
};
struct Point
{
  db x, y;
  int id;
  Vec operator - (const Point& oth)const
  {
    return (Vec){x - oth.x, y - oth.y};
  }
  friend void swap(Point& A, Point& B)
  {
    swap(A.x, B.x); swap(A.y, B.y);
  }
}p[maxn], S;
inline bool cmp(Point A, Point B)
{
  db s = (A - S) * (B - S);
  if(fabs(s) > eps) return s > eps;
  return dis(A - S) - dis(B - S) < -eps;
}

db solve(Point A, Point B, Point C)
{
  return (B - A) * (C - A);
}

void init()
{
  int id = 1;
  for(int i = 2; i <= n; ++i)
    if(p[i].x < p[id].x - eps || (fabs(p[i].x - p[id].x) < eps && p[i].y < p[id].y)) id = i;
  if(id != 1) swap(p[1], p[id]);
  S.x = p[1].x; S.y = p[1].y;
  for(int i = 1; i <= n; ++i) p[i].id = i;
  sort(p + 2, p + n + 1, cmp);
}

int st[maxn], top = 0;
db ans = 0;

int main()
{
  n = read();
  for(int i = 1; i <= n; ++i) scanf("%lf%lf", &p[i].x, &p[i].y);
  init();
  st[++top] = 1;
  for(int i = 2; i <= n; ++i)
    {
      while(top > 1 && solve(p[st[top - 1]], p[st[top]], p[i]) < -eps) top--;
      st[++top] = i;
    }
  st[top + 1] = st[1];
  for(int i = 1; i <= top; ++i)
    ans += sqrt(dis(p[st[i + 1]] - p[st[i]]));
  printf("%.2lf\n", ans);
  return 0;
}

然后我因为极点没赋初值\(Debug\)了不知多长时间……