小白初识 - 计数排序（CountingSort）

计数排序，属于桶排序特殊的一种。

当要排序n个数据的时候，如果所处的范围不大，我们可以取其中的最大值K，并将数据分散在K个桶里面，

每个桶里面的数据都是相同的（这样省去了桶内排序的时间），然后顺序取出就好啦。

当然计数排序说起来简单，写起来有些地方不好理解。

比如我们现在有2，5，3，0，2，3，0，3这8个数，要对它排序，我们就可以先取到它的最大值5，然后确定范围在0-5，

我们申请一个0-5的内存空间去分别计算每个位置对应的每个数的个数。

下图表示的就是0-5这个内存空间的数据，我们可以看到其中0出现了两次，1出现了0次，2出现了两次，3出现了三次，4出现了0次，5出现了一次。

同时还可以总结一些规律出来，比如我们现在看到c[2]这个位置，2出现了两次，在2前面c[0] + c[1]总共有2个元素，所以c[2]对应这两个2在原数组中

的位置是2，3，我们可以得出规律c[2]所在位置 = c[0] + c[1]，后面的c[3]的位置 = c[2] + c[1]，我们就这样挨着顺序求和：

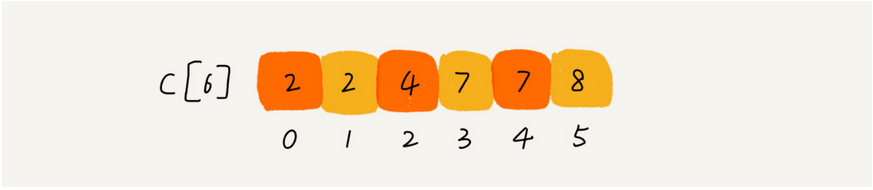
然后我们扫描原数组2，5，3，0，2，3，0，3，每遇到一个数，就将该数代入c数组的索引中取出当前元素在排序之后真正的索引。

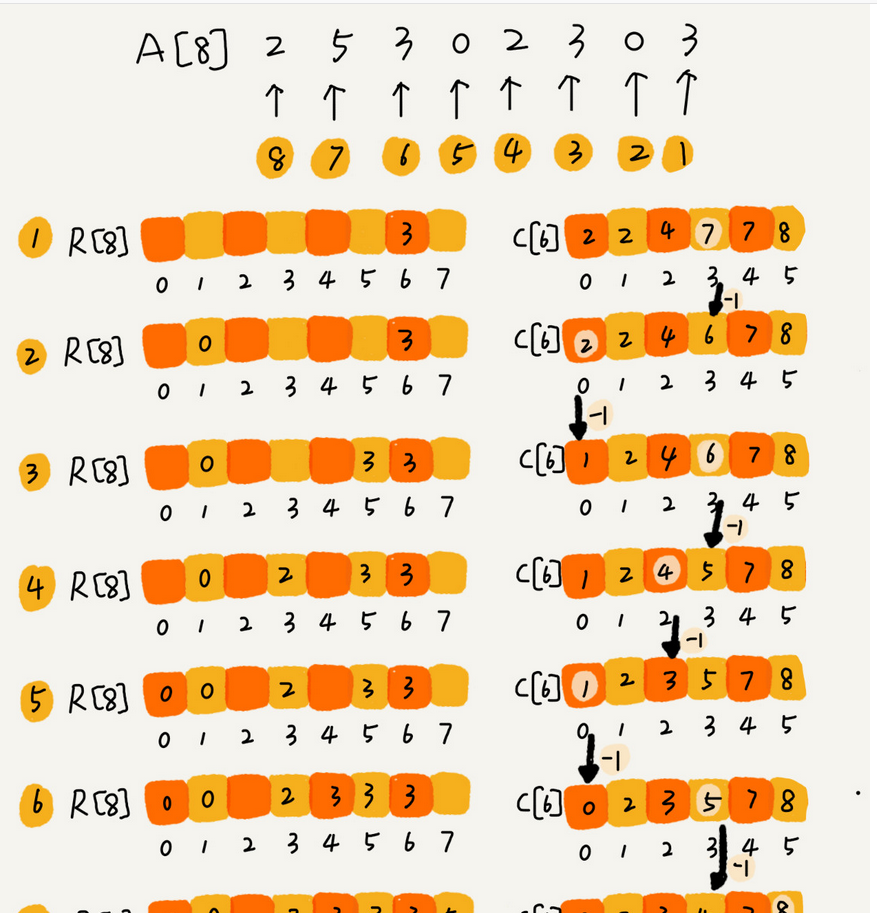
我的Java实现如下：

 package com.structure.sort;

 /**
  * @author zhangxingrui
  * @create 2019-01-30 13:45
  **/
 public class CountingSort {

     public static void main(String[] args) {
         int[] numbers = {3, 9, 2, 1, 8, 7, 6, 10, 9};
         // 假设数组中存储的都是非负整数
         countingSort(numbers);
         for (int number : numbers) {
             System.out.println(number);
         }
     }

     /**
      * @Author: xingrui
      * @Description: 计数排序
      * @Date: 13:57 2019/1/30
      */
     private static void countingSort(int[] numbers){
         int n = numbers.length;
         int maxNumber = numbers[0];
         for(int i = 1; i < n; ++i){
             if(numbers[i] > maxNumber)
                 maxNumber = numbers[i];
         }

         int[] r = new int[n];
         int[] c = new int[maxNumber + 1];

         for(int i = 0; i < n; ++i){
             c[numbers[i]]++;
         }

         for(int i = 1; i <= maxNumber; ++i){
             c[i] = c[i-1] + c[i];
         }

         for (int i = n - 1; i >= 0; --i){
             int index = c[numbers[i]];
             r[index - 1] = numbers[i];
             c[index]--;
         }

         for(int i = 0; i < n; ++i){
             numbers[i] = r[i];
         }
     }

 }

其中关键的代码：

 for (int i = n - 1; i >= 0; --i){
             int index = c[numbers[i]];
             r[index - 1] = numbers[i];
             c[index]--;
         }

从c数组中取出排序之后的索引。

需要特别说明的是，文中的图片均截图极客网王争老师的专栏《数据结构与算法之美》，如有侵权，请联系我删除。

有需要的朋友也可以去订阅这个专栏，讲的挺不错的，没有视频，只有文字和音频。