2-3-4树（jdk8的TreeMap的红黑树）

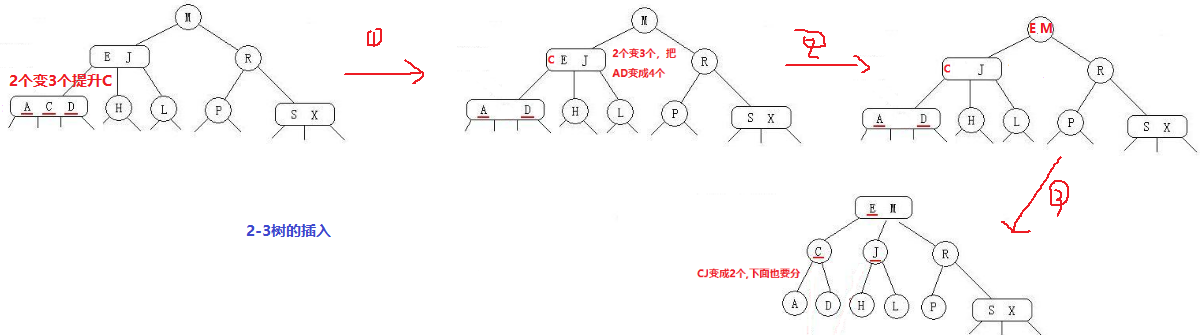
2-3树：插入变成2个节点正常插，变成3个节点就要提升中间节点和分裂子节点，满足：要么没有子节点，要么2个子节点，要么3个子节点。

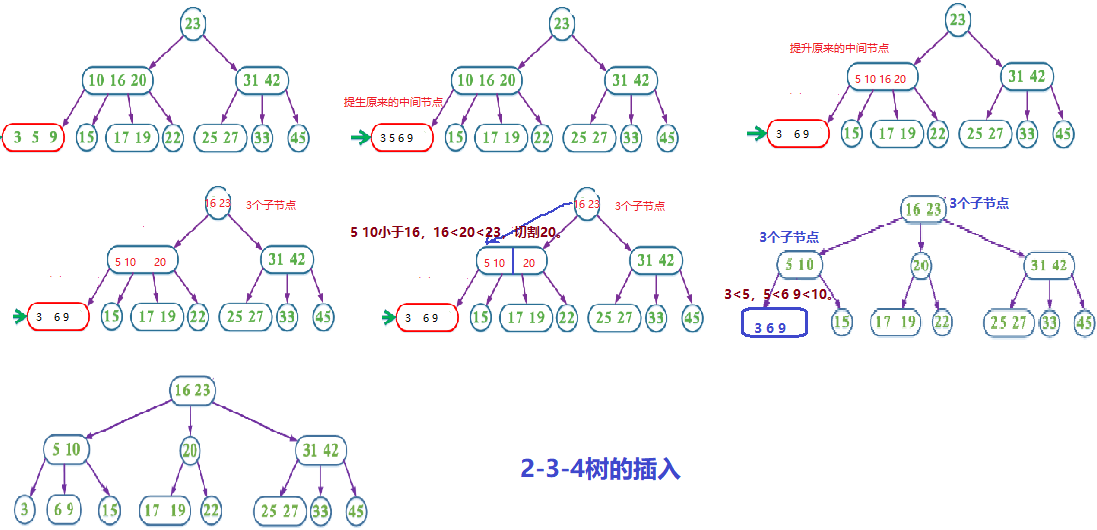
2-3-4树：插入变成2个不动，插入变成3个不动，插入变成4个提升原来中间节点和分裂子节点，满足：要么没有子节点，要么2个子节点，要么3个子节点，要么4个子节点。

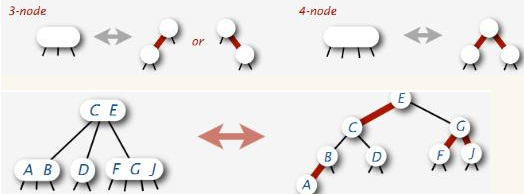
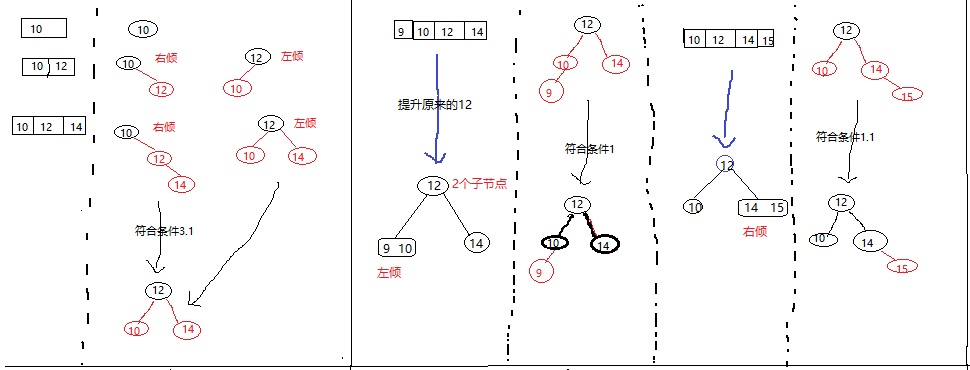
2节点黑色，3节点左倾和右倾，4节点上黑下2红。

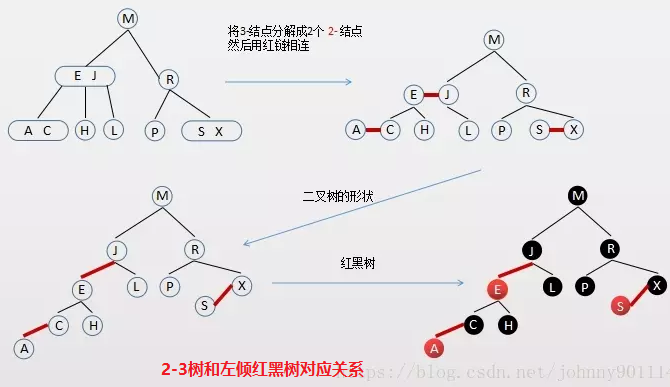
左倾2-3树：2节点黑色，3节点左下红右上黑。

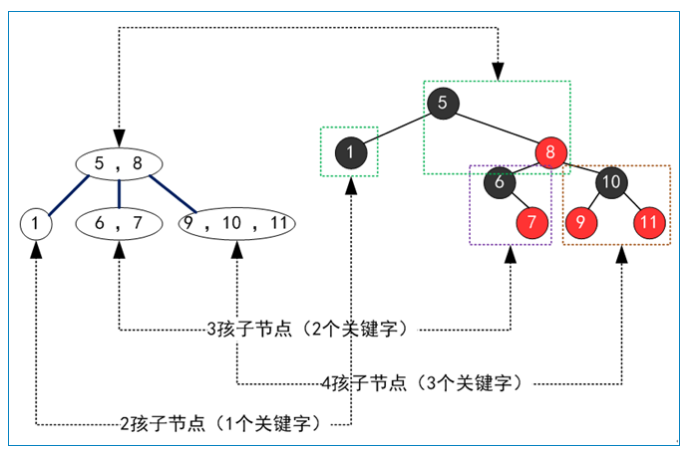
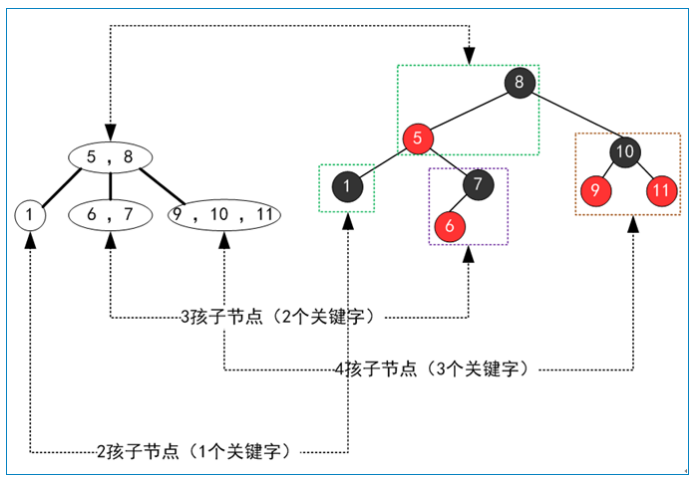
红黑树插入和2-3-4树的对应关系：

先插入10再插入12，所以是右倾。

先提升12分裂10和14，所以10在12子节点上，在加上9，所以是左倾。       再加上15，因为14在12子节点上，所以是右倾。      

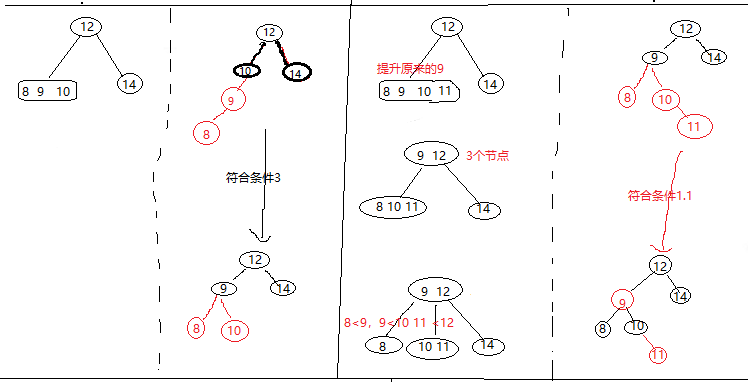
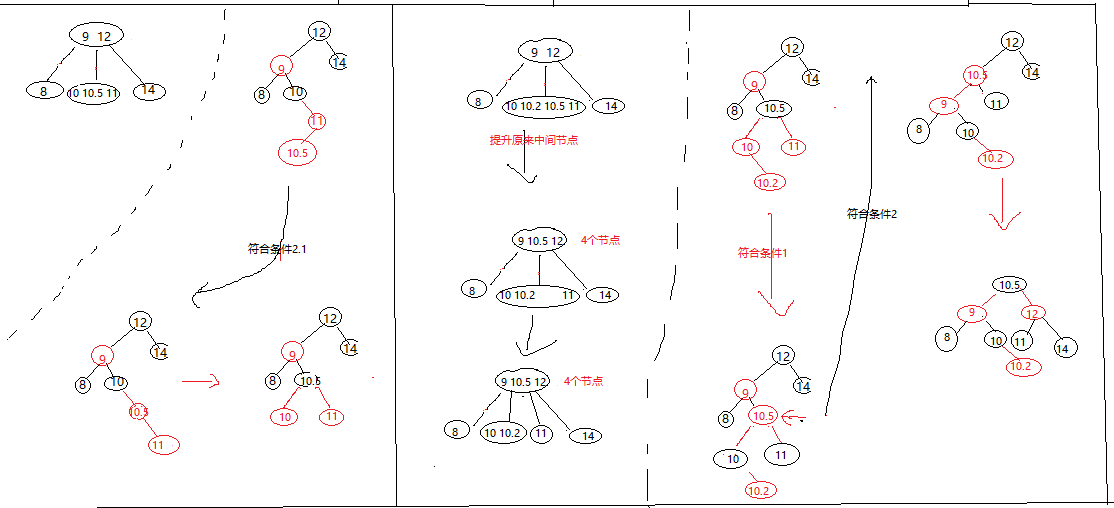
2-3-4树只是规定了普通红黑树最终的样子和颜色，中间调整规则  是通过2-3-4树推到出来的，规则如下：

JDK1.8  TreeMap的红色树插入规则：

1.父亲是黑色，退出

2.父亲是红色

　　2.1爷爷左边

　　　　2.1.1爷爷右节点是红色 条件1

　　　　　　父亲变黑，爷爷右节点变黑，爷爷变红，x指向爷爷继续判断

　　　　2.1.2爷爷右节点是黑色

　　　　　　2.1.2.1父亲右边    条件2

　　　　　　　　左旋父亲 —> 2.1.2.2父亲左边 条件3

　　　　　　　　　　父亲变黑，爷爷变红，右旋转爷爷

　　2.2爷爷右边

　　　　2.2.1爷爷左边红色 条件1.1

　　　　　　父亲变黑，爷爷左边变黑，爷爷变红，x指向爷爷继续判断

　　　　2.2.2爷爷左边黑色

　　　　　　2.2.2.1父亲左边 条件2.1

　　　　　　　　右旋转父亲 —> 2.2.2.2父亲右边 条件3.1

　　　　　　　　　　父亲变黑，爷爷变红，左旋转爷爷

case 1. 根结点，设为黑色，结束

case 2. 父黑色，不调整，结束

case 3. 叔叔红色，插入节点可左可右：父黑叔叔黑，爷爷红，指向爷爷再看（颜色调整）。

case 4. 叔叔黑色：

　　　　父节点左右和爷爷节点左右不在同一边，先旋转父节点到同一边。

　　　　父黑爷爷红（颜色调整），反向旋转爷爷。

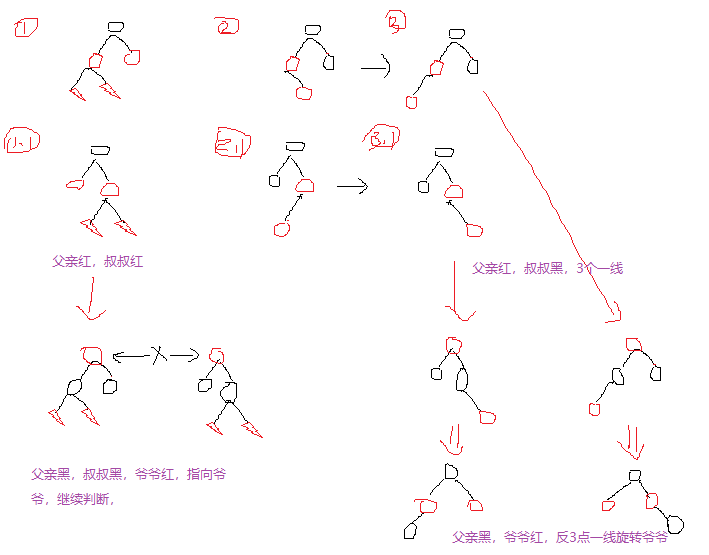
红黑树(对应2-3-4树)和左倾红黑树(对应2-3树)

普通红黑树：允许一个节点有两个红色的子节点

左倾红黑树：一个节点只能有一个红色子节点，并且是左节点

普通红黑树(以下简称红黑树)对应2-3-4树

左倾红黑树对应2-3树

2-3-4树呢?顾名思义，就是有2个子女，3个子女，或4个子女的结点，这些含有2、3、或4个子女的结点就构成了我们的2-3-4树。

一颗红黑树对应唯一形态的2-3-4树，但是一颗2-3-4树可以对应多种形态的红黑树（主要是3节点可以对应两种不同的红黑树形态）

红黑树（普通红黑树，不是左倾红黑树）的五个性质：

1）每个结点要么是红的，要么是黑的。

2）根结点是黑的。

3）每个叶结点，即空结点（nil）是黑的。

4）如果一个结点是红的，那么它的俩个儿子都是黑的。

5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。

左倾红黑树：

1. 红链接均为左链接。
2. 没有两条红链接相连。
3. 任意空链接到根结点的路径上的黑链接数量相同。

传送门：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html