SIGAI机器学习第二十一集 AdaBoost算法2

讲授Boosting算法的原理,AdaBoost算法的基本概念，训练算法，与随机森林的比较，训练误差分析，广义加法模型，指数损失函数，训练算法的推导，弱分类器的选择，样本权重削减，实际应用。

大纲：

广义加法模型
指数损失函数
AdaBoost训练算法的推导
实现细节问题
弱分类器的选择
弱分类器的数量
样本权重削减

上节课我们介绍了AdaBoost算法的训练算法和预测算法，其中训练算法还是一个很精密的过程，这个算法是怎么想出来的有没有什么依据？包括弱分类器的权重为什么是1/2log(1-et)/et？样本权重的更新公式为什么是那样的？它们都是有理论依据的。

可以把AdaBoost算法和微积分来对比，它们两个其实非常类似。微积分它是先有方法，先有一些计算公式然后再补充的理论，微积分发明的时候有很多不严密的地方包括牛顿本人他就没法解释无穷小是怎么回事一会可以当作0一会不能当作0，整个微积分它的严密的体系是柯西给建立的，其中非常核心的就是建立了极限这个概念的严格的定义，ε-δ这种定义方式。而AdaBoost算法和这个类似，他也是先有了方法，然后再有了理论解释，它是用广义加法模型和指数损失函数相结合的一个产物来解释的，也就是用广义加法模型来求解指数损失函数，最后就导出了我们的AdaBoost算法的训练算法。

广义加法模型：

广义加法模型拟合的目标函数是多个基函数的线性组合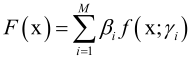，，f是基函数，带有参数γ_i和权重βi（βi>0），基函数f具体什么形式是不知道的（是一次函数还是二次函数等都是不知道的），一旦确定了f的形式，算法要确定的就是γi、βi两组参数。

F(x)就非常像我们的AdaBoost的强分类器了，强分类器就是很多弱分类器的线性组合而形成的。γi、βi参数也是通过训练算法来确定的，和其他有监督的机器学习算法没有什么两样，这里只不过把我们要拟合的F(x)拆成很多函数加权和的形式，其他的和我们标准的有监督学习算法一模一样的。定义了一个损失函数，它是定义在所有的样本上的，有l个样本，我们是要所有的样本误差最小化。

模型的参数包括基函数的参数以及权重，通过训练算法得到。训练时优化的目标是对所有样本的损失函数：

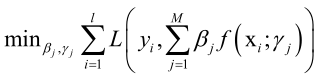
其中F(x)写成加权和的形式，这其实就是有监督学习训练的时候的一个标准的损失函数，这里为什么要用加法不写成乘法形式呢？因为加法实现起来很简单，而且加法比乘法稳定，假设基函数有100个的话，基函数输出值为0~100的话，那么很快它的输出值就爆炸了乘起来会产生一个非常大的数，这样是不太好的。

在定义了广义加法模型训练的时候的优化的损失函数之后，接下来就是怎么求解他了，这里求解采用了一个特殊的技巧，和一般的机器学习算法不一样，是逐步迭代（依次求出每个小的基函数f(x)即它的系数值），即先求f1它的参数，γ1以及它的权重β1，求完以后，再紧接着求f2的、f3...一直往后求，每累加一个基函数上去，这个模型F(x)的精度就会越来越高，所以说它是迭代完成训练过程的，每次优化一个基函数的参数以及它的权重系数。

总结一下，广义加法模型是一个抽象的框架，他把我们要拟合的目标函数F(x)表示成一系列小的函数的加权和，然后f(x)的形式是不知道的，因此可以从这个抽象的框架导出各种各样的机器学习算法来。除了f(x)是不知道的以外损失函数L(x)也是不知道的，如果我们对f(x)和L(x)具体化的话，我们可以得到一些具体的机器学习的算法，比如说AdaBoost算法。

指数损失函数：

AdaBoost整个训练过程是从广义假发模型和指数损失函数这两个东西导出来的，指数损失函数定义：

y是样本的真实标签值，F(x)是模型对它的预测值，对于AdaBoost算法而言F(x)是强分类器，为什么这么定义呢？它是有道理的，对于二分类问题y要么取+1要么取-1，取+1时强分类器越是接近于+1越是大于0，-yF(x)是大于0的数乘以大于0的数取负号则为小于0，exp(-yF(x))的值就越小，反之样本标签值y为负数的话只有当F(x)取负的时候exp(-yF(x))的值才会越来越小，总之保证y和F(x)尽量的同号，exp(-yF(x))的函数值才会越来越小，即模型的预测值与样本的真实标签值越接近，其值越小，因此他会迫使我们训练出来的强分类器F(x)和y尽可能的接近，也就是说他们的负号至少要是一致的，要么都是正的要么都是负的，AdaBoost算法可以由广义加法模型+指数损失函数导出，接下来就进行完整的推导。

AdaBoost训练算法的推导：

广义假发模型它是用迭代法反复的来迭代，依次来计算每个基函数它的参数值和它的权重系数，在推导AdaBoost算法的时候也采用了同样的策略，我们把AdaBoost算法强分类器的形式带到指数损失函数里边去。

假设现在要进行第j次迭代，前边j-1个基函数弱分类器已经算出来了，接下来我们要优化第j个弱分类器，包括它的参数以及它的权重。训练时优化目标是最小化损失函数：

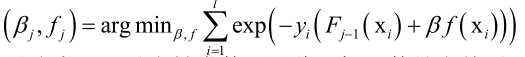
前边j-1个基函数已经算出来了，所以Fj-1可以当成一个常数值，而βf(xi)是我们真正要优化的目标。

之前得到的强分类器可以当做常数，因此目标函数是当前要训练的弱分类器、弱分类器系数的函数：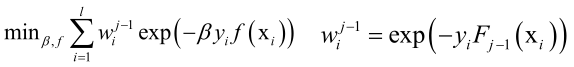

怎么优化呢？采用分阶段优化策略。

首先将弱分类器权重当做常数，寻找最优的弱分类器，找到弱分类器f之后，再把f当作一个常数，再优化β，把β当作我们要优化的变量。

只有当弱分类器的预测值与样本的真实标签值一致时，函数有极小值：

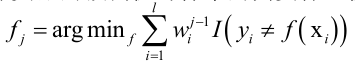
得到弱分类器之后，再优化它的系数：

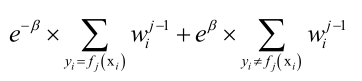
目标函数可以写成：

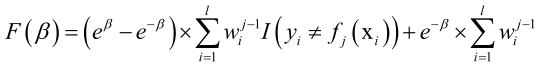
F(β)在极值点处导数必须为0：

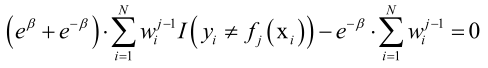
得到下面的方程：

最优解为：

则就算出了弱分类器的权重β值。

在得到新的弱分类器的参数和权重之后，将其累加到之前的强分类器上去就得到新的强分类器，做更新就得到下一步迭代的基础了，即在Fj(x)的基础上迭代。

导致下次迭代时样本的权重为：

实现细节问题：

在推导完整个AdaBoost算法它的整个训练算法的来历以后，接下来看几个细节的问题：

弱分类器的选择
弱分类器的数量
样本权重削减，对于前边分类正确的样本它的权重会随着迭代而下降，降很多次之后会慢慢的接近于0，这些样本该怎么处理呢。

弱分类器的选择：

弱分类器之所以叫弱分类器，是因为它能力非常弱，不需要它的精度很高，只要能保证它的准确率大于0.5就可以了，因此我们就不用用一些非常强的分类器来做这里的弱分类器了（比如用SVM、神经网络做弱分类器，虽然理论上还是可行的，但是不是很合适）。

强分类器是弱分类器的线性组合，所以我们的弱分类器必须是非线性的，如果都是线性的话，组合起来还是一个线性的模型，这样的话，能力太弱了，实际我们在工程实现的时候一般选用决策树来做弱分类器，而且决策树的深度还非常小，比如我们可以用深度为1（只有一个内部发展节点和两个叶子节点）的决策树，即使我们用这样很简单的弱分类器来组合，也可以形成一个精度非常高的强分类器，这是得利于弱分类器它带有权重值a以及在训练fi(x)的时候它重点关注了前边被错分的样本，这是和随机森林很不一样的地方。只有一个内部节点的决策树（深度为1的决策树），我们称为桩分类器（stump分类器）。

弱分类器的数量：

前面推导了一个结论，随着弱分类器的数量的增加，强分类器在训练样本集上的误差会呈指数级的下降，一般来说它在测试样本集上也是呈这种指数级下降，因为泛化性能它不是理想化的有过拟合问题存在，所以一般在测试样本集上的表现要比训练集上要差一些的，这个观点可以指导我们选择弱分类器的数量，我们可以通过算法来确定弱分类器的数量，我们在训练的过程中用一个样本集来测试或者直接在训练样本集上测试，一旦他的误差或准确率大于某个指定的阈值的话就可以停止迭代了，后边在讲目标检测算法的时候会看到这个具体的实现，也就是说要让目标检测的准确率大于某一个阈值比如说0.95的话我们就可以停止迭代就到此为止训练这么多弱分类器就OK了。另一种方案更简单粗暴，就是人工指定一个值，但是这个一般不是很常用。

样本权重削减：

随着迭代的进行，被正确分类的样本权重(每次都会乘以一个小于1的数，虽然经过规范化归一化)越来越小，趋向于0，对后续的训练作用不大，可以剔除这些权重非常小的样本，这称为样本权重的削减。
具体怎么实现呢？可以对样本的权重值从大到小进行排序，比如可以把最小的1%的样本给剔除掉。