Linear Algebra Lecture5 note

Section 2.7     PA=LU

and Section 3.1   Vector Spaces and Subspaces

 

---

Transpose(转置）

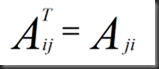
example:

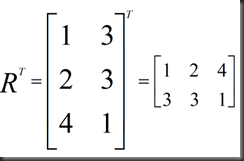
特殊情况，对称矩阵（symmetric matrices),例如：

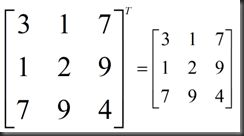
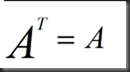
思考：R^R(R的转置乘以R)有什么特殊的？

回答：always symmetric

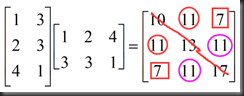
why?

 

---

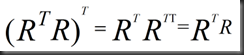
Permutation（置换）

P=execute row exchanges

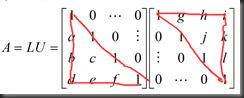
之前A=LU是建立在no row exchanges 的基础上的，但不可能每一个矩阵都是完美的，有些矩阵需要通过行变换处理，

即PA=LU （any invertible A）

P= indentity matrix with reordered rows

置换矩阵是重新排列了的单位矩阵

counts reorderings(counts all the n * n permutations : n!

性质：

 

---

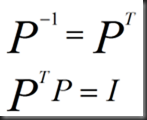
Vector Spaces

Example:

R^2= all 2 dimensional real vectors = “x-y”plane,

 

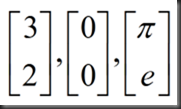
R^3= all vectors with 3 component

R^n = all vectors with n component

思考：not  a  vector space? what’s the condition?

回答：向量空间必须对数乘和加法两种运算是封闭的（线性组合封闭）

比如说，二维平面子空间  line in R^2 through zero vector

总结：

subspaces of R^2: all of R^2(itself), any line through zero vector (L), zero vector only (Z)

subspaces of R^3: all of R^3(itself), any plane through zero vector (P), any line through zero vector (L), zero vector only (Z)

example:

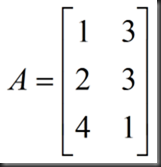
cols in R^3, all their combinations form a subspace called column space, C(A)