使用OpenCV&&C++进行模板匹配.
一:课程介绍
1.1:学习目标
- 学会用imread载入图像,和imshow输出图像。
- 用nameWindow创建窗口,用createTrackbar加入滚动条和其回调函数的写法。
- 熟悉OpenCV函数matchTemplate并学会通过该函数实现模板匹配。
- 学会怎样将一副图片中自己感兴趣的区域标记出来
1.2:什么是模板匹配?
在一副图像中寻找和另一幅图像最相似(匹配)部分的技术。
1.3:案例展示
输入有两幅图像一副是 template.jpg 另一幅是 original.jpg 。匹配完成的结果是result.jpg
二:实验原理
让模板图片在原图片上的一次次滑动(从左到右,从上到下一个像素为单位的移动),然后将两张图片的像素值进行比对,然后选择相似度最高的部分进行标记,当遇到相似度更高的部分时更换标记部分。扫描完毕之后,将相似度最高的部分标记出来,作为图片进行输出操作。
三:环境搭建
$ cd ~
$ sudo apt-get update
$ wget http://labfile.oss.aliyuncs.com/courses/671/opencv.sh
$ sudo chmod 777 opencv.sh
$ ./opencv.sh
在执行完之后执行如下语句,检查是否安装成功
./facedetect --cascade="/usr/local/share/OpenCV/haarcascades/haarcascade_frontalface_alt.xml" --scale=1.5 lena.jpg
四:实验步骤
4.1定义头文件
在这里我们用了
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
这三个头文件:
highgui.hpp:定义了创建窗口的flag,窗口事件的flag,Qt窗口的flag,事件回调函数原型,以及窗口/控件操作相关的系列函数,openGL的包装函数;图像输入输出显示的相关函数;视频摄像头输入输出显示的相关函数,VideoCapture,VideoWriter。
imgproc.hpp:定义了图像处理模块之平滑和形态学操作。
iostream:不再赘述。
4.2:设计主要功能并对其解析(从main函数入口开始分析)
imread函数:
img = imread("original.jpg");//载入元图像
templ = imread("template.jpg");//载入模版图像
imread函数可以将图片读取然后放到Mat容器里面用于后续操作。
nameWindow函数:
namedWindow( image_window, CV_WINDOW_AUTOSIZE ); // 窗口名称,窗口标识CV_WINDOW_AUTOSIZE是自动调整窗口大小以适应图片尺寸。
namedWindow( result_window, CV_WINDOW_AUTOSIZE );
创建窗口。第一个参数是窗口名称,第二个窗口是int类型的Flag可以填写以下的值
- WINDOW_NORMAL设置了这个值,用户便可以改变窗口的大小(没有限制)
- WINDOW_AUTOSIZE如果设置了这个值,窗口大小会自动调整以适应所显示的图像,并且不能手动改变窗口大小
createTrackba函数:
/// 创建滑动条
createTrackbar("匹配方法", image_window, &match_method, max_Trackbar, MatchingMethod ); //滑动条提示信息,滑动条所在窗口名,匹配方式(滑块移动之后将移动到的值赋予该变量),回调函数。
创建滑动条,第一个参数是匹配方法,第二个参数是确定滑动条所在窗口,第三个参数是对应滑动条的值,第四个参数是滑动条的最大值,第五个参数是回调函数。
自己写的回调函数
MatchingMethod( 0, 0 );//初始化显示
先调用回调函数,在没有滑动滑块的时候也有图像。
waitkey函数:
waitKey(0); //等待按键事件,如果值0为则永久等待。
其取值可以是<=0或大于0.当取值为<=0的时候,如果没有键盘触发则一直等待,否则返回值为按下去的ascll对应数字。
Mat::copyto函数:
Mat img_display;
img.copyTo( img_display ); //将 img的内容拷贝到 img_display
创建Mat类型数据结构img_display。并将img内容赋值给img_display。
Mat::create函数:
/// 创建输出结果的矩阵
int result_cols = img.cols - templ.cols + 1; //计算用于储存匹配结果的输出图像矩阵的大小。
int result_rows = img.rows - templ.rows + 1; result.create( result_cols, result_rows, CV_32FC1 );//被创建矩阵的列数,行数,以CV_32FC1形式储存。
matchTemplate (模版匹配)函数
matchTemplate( img, templ, result, match_method ); //待匹配图像,模版图像,输出结果图像,匹配方法(由滑块数值给定。)
我们在createTrackba函数那里见到过match_method变量,这个是决定匹配方法的变量,由滑块确定。
normalize(归一化函数)
normalize( result, result, 0, 1, NORM_MINMAX, -1, Mat() );//输入数组,输出数组,range normalize的最小值,range normalize的最大值,归一化类型,当type为负数的时候输出的type和输入的type相同。
归一化就是要把需要处理的数据经过处理后(通过某种算法)限制在你需要的一定范围内。首先归一化是为了后面数据处理的方便,其次是保证程序运行时收敛加快。归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的概率分布,归一化在某个区间上是统计的坐标分布。归一化有同一、统一和合一的意思。
minMaxLoc函数
minMaxLoc( result, &minVal, &maxVal, &minLoc, &maxLoc, Mat() );//用于检测矩阵中最大值和最小值的位置
用于寻找距震中的最大值和最小值
不同方法之间选择最佳精确度
if( match_method == CV_TM_SQDIFF || match_method == CV_TM_SQDIFF_NORMED )
{ matchLoc = minLoc; }
else
{ matchLoc = maxLoc; }
对于方法CV_TM_SQDIFF,和CV_TM_SQDIFF_NORMED,越小的数值代表越准确匹配结果,而对于其他方法,数值越大匹配的准确度越高。
将最后得到的结果显性的标记出来
/// 让我看看您的最终结果
rectangle( img_display, matchLoc, Point( matchLoc.x + templ.cols , matchLoc.y + templ.rows ), Scalar(0,0,255), 2, 8, 0 ); //将得到的结果用矩形框起来
rectangle( result, matchLoc, Point( matchLoc.x + templ.cols , matchLoc.y + templ.rows ), Scalar(0,0,255), 2, 8, 0 );
第一个参数(img):将要被操作的图像,第二个和第三个参数分别是一个矩形的对角点。第四个(color)参数是线条的颜色(RGB)。第五个参数(thickness):组成矩阵线条的粗细程度。第六个参数(line_type):线条的类型,见cvLine的描述。第七个参数shift:坐标点的小数点位数
4.3:应用算法解析
matchTemplate实现了末班匹配散发:其中可用的方法有六个:
1: 平方差匹配: method = CV_TM_SQDIFF
这类方法利用平方差来进行匹配最好匹配为0.匹配差越大,匹配值越大。
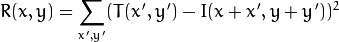
2: 标准平方差匹配:method = CV_TM_SQDIFF_NORMED
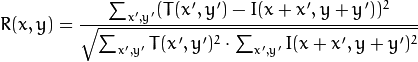
这类方法利用平方差来进行匹配最好匹配为0.匹配差越大,匹配值越大。
3: 相关匹配method=CV_TM_CCORR
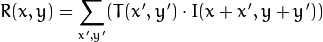
这类方法采用模板和图像间的乘法操作,所以较大的数表示匹配程度较高,0标识最坏的匹配效果.
4: 标准相关匹配 method=CV_TM_CCORR_NORMED
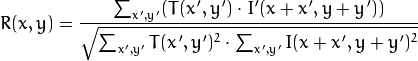
同标准平方差和平方差,以下不再赘述。
5: 相关匹配 method=CV_TM_CCOEFF
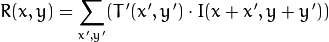
这类方法将模版对其均值的相对值与图像对其均值的相关值进行匹配,1表示完美匹配,-1表示糟糕的匹配,0表示没有任何相关性(随机序列).
6: 标准相关匹配 method=CV_TM_CCOEFF_NORMED
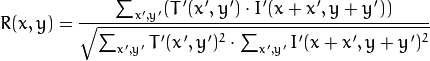
通常,随着从简单的测量(平方差)到更复杂的测量(相关系数),我们可获得越来越准确的匹配(同时也意味着越来越大的计算代价). 最好的办法是对所有这些设置多做一些测试实验,以便为自己的应用选择同时兼顾速度和精度的最佳方案.
有了上述相关知识之后相信你就可以看懂并且对下方代码进行改造的能力了
五:试验程序
这里就是完整的代码,上面对这些代码已经做了完整的解析。
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream> using namespace std;
using namespace cv; Mat img; Mat templ; Mat result;
char* image_window = "Source Image"; //窗口名称定义
char* result_window = "Result window"; //窗口名称定义 int match_method;
int max_Trackbar = 5; void MatchingMethod( int, void* )
{ Mat img_display;
img.copyTo( img_display ); //将 img的内容拷贝到 img_display /// 创建输出结果的矩阵
int result_cols = img.cols - templ.cols + 1; //计算用于储存匹配结果的输出图像矩阵的大小。
int result_rows = img.rows - templ.rows + 1; result.create( result_cols, result_rows, CV_32FC1 );//被创建矩阵的列数,行数,以CV_32FC1形式储存。 /// 进行匹配和标准化
matchTemplate( img, templ, result, match_method ); //待匹配图像,模版图像,输出结果图像,匹配方法(由滑块数值给定。)
normalize( result, result, 0, 1, NORM_MINMAX, -1, Mat() );//输入数组,输出数组,range normalize的最小值,range normalize的最大值,归一化类型,当type为负数的时候输出的type和输入的type相同。 /// 通过函数 minMaxLoc 定位最匹配的位置
double minVal; double maxVal; Point minLoc; Point maxLoc;
Point matchLoc; minMaxLoc( result, &minVal, &maxVal, &minLoc, &maxLoc, Mat() );//用于检测矩阵中最大值和最小值的位置 /// 对于方法 SQDIFF 和 SQDIFF_NORMED, 越小的数值代表更高的匹配结果. 而对于其他方法, 数值越大匹配越好
if( match_method == CV_TM_SQDIFF || match_method == CV_TM_SQDIFF_NORMED )
{ matchLoc = minLoc; }
else
{ matchLoc = maxLoc; } /// 让我看看您的最终结果
rectangle( img_display, matchLoc, Point( matchLoc.x + templ.cols , matchLoc.y + templ.rows ), Scalar(0,0,255), 2, 8, 0 ); //将得到的结果用矩形框起来
rectangle( result, matchLoc, Point( matchLoc.x + templ.cols , matchLoc.y + templ.rows ), Scalar(0,0,255), 2, 8, 0 ); imshow( image_window, img_display );//输出最终的到的结果
imwrite("result.jpg",img_display); //将得到的结果写到源代码目录下。
imshow( result_window, result ); //输出匹配结果矩阵。 return;
} int main( int argc, char** argv )
{ img = imread("original.jpg");//载入待匹配图像
templ = imread("template.jpg");//载入模版图像 /// 创建窗口
namedWindow( image_window, CV_WINDOW_AUTOSIZE ); // 窗口名称,窗口标识CV_WINDOW_AUTOSIZE是自动调整窗口大小以适应图片尺寸。
namedWindow( result_window, CV_WINDOW_AUTOSIZE ); /// 创建滑动条
createTrackbar("jackchen", image_window, &match_method, max_Trackbar, MatchingMethod ); //滑动条提示信息,滑动条所在窗口名,匹配方式(滑块移动之后将移动到的值赋予该变量),回调函数。 MatchingMethod( 0, 0 );//初始化显示 int logo = waitKey(5000); //等待按键事件,如果值0为则永久等待。 return 0;
}
六:完整实验流程
在源代码存放的文件夹里面有两幅图片,一幅original.jpg是待匹配的图片,另一幅是template.jpg是模版图片,然后输出一副匹配成功的图片。
一下分别是 original.jpg,template,result.jpg

aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wgARCAGLAYIDASIAAhEBAxEB/8QAGwAAAgMBAQEAAAAAAAAAAAAABAUCAwYBAAf/xAAaAQADAQEBAQAAAAAAAAAAAAACAwQBAAUG/9oADAMBAAIQAxAAAAHC+95i/c7zud1qvD0fd8Xe972d7nu73O+9mztrvX0LeXrdA/zCXHx3PeJULj9Agv8AYv0eW1DZtNVOhflUwtHidbGEcKzvI6Q06LWMqStwHdKqFLzaC3jh3SgCMGAV0WKSMVxrxI9T4NzXvd9bzOe7zu973u73vd7ue7zu5PhObQS1nJUivnPl+OldNeaw84iTMU1Eo0Ys6/Q9rumym12B2suXwQMBSBpGhFoGddJ3F3BC+1JYxjJZMVmdqlXQJc1vO5/UsrVxUQLXIQsBmNCqvWeWxD33vS83nfd7Oe77O9yXu6Ppe7esgniTraU3eZ6aQu20w7PtKq9A5Xnz+fTldFkrqxvQ4fpd0mdLGZ2ULdBFNbTWylW+yekpEmiNycSiO0lXFDhdZjSae8VtO0wAypgMA3xg1y058wcqkJ+n4Ny/u+9TzPP0Fg76He7kfS73RlIge5o1r+Ci0N+kh9AKmE6XyJCK5enJsG2NTm2CV3pzlGWVSjxcUulKTuJlWyIqHMWVGizdZBadKPgDlx9Qs0oRii7cJVI16sJW045WQlp9y81KxpxYlgfpeLsn33fU8z3vSHud73s5P1udwqJqSMa1H+Ta2zemzJUIoEBV2y0me2qp2itnn2SZOuM2evZLnRbQtNXP83SvFej83CUGkyIYnBPXelS5NzuvBS0oOoR1tGd9MF+fdLaDV+vprmvKV3DzFgqOm3jIafaV5V4SRe931PK733czsuTHu3xKXtjgbQwN4XXdBSTldPkbaVghQtF+q0YLWTyqMbr8C5oVldjvStr7DiEL6wKM/SqnHnz9w+wwhOgEZTbSy0Ahi58koODoW6eoD5WPFlKgMKXmhUAvrIopk6xUEYvTVAky1T9Z5bc93vfU8X0uTzvWRvDbWI7CZpDdATFfNulczkRk9Vjb2r7R9YVL06uSPGSYjS5h3q+lzrKfd7DtqaZ/SM85+5UtfLUoyLhLZfVRPzg2VTBJGGYDMo9GeTyDVTlc1pmc/LTkR5Uk0gx9jIPkV8V5YB2E18H6atdL3fQ8T0vWD3jKWCjtulGP0GNNicbWN6BgstFitZkKdH+h/PPo4zsK5hTw5BQyW1+x2cek3w14JKF12R3W+e9jYn8gkPKq/U9Kkla52fZYvSZOThGomhtXNMciW6qY9FEbmtNcIubVMFUFBc45Q5QcmQn+55T+9n5/nctjaHWnjmzVF3UkS3zR7HPsdn7JCMfpc65R9jPc5/RRef4K4WkMWNZW/wBOfI9xvl5YLIvb7KbOMZ5pxmgfyPBrW90yDWIUpX8rJtOzyGwZNmQbASLgvu0eTIqwlVoFx9gNTCP0rI6O862XvvezW3ezFPL+Ehtpwz6ZtabSJE+noaF2gBOJDZraPUKXkr2L+gnAGeZ5ogJie+jNx9Q6q2VMe7g1sXQt3y4qSxaPyBv9T7hpZMh1qWx9yDMNJKznI8MbwxWvnGh2PHr3+WCzmsyzIFO87oISnhIHA+t5nfc9q3tnLErsKpKURD1e7gokpO5PRltYLY468ZuM2+hNVHljdqekbQyVg+Ae9BR2ukJdrnoQt8ThsRPAraRz3NZ44J3y6F8qxd4sVtqxA+jb0nKbSYD8AZNONa7glqdmwwLyYXkCCpHJsn9Eyjdz3rPen57y2V0sfjqWCWGNBb5XwXFrSob5ss7GjAjSqZnx2ientE/w2miPi28ChinnYU+b3kOEswsWlVkrRpEu/ojcTMDqqCm/weo7PJ/D4cgJOmynQGETTITy5qOT7N3nWHWVovjoUFyHaMFYQrFvjPUaUSCYvwCzRmMjz/U2z0V+FQUNMBjVRYaGWreNa2+tiRdHP6DyUNGi6oMPmfqigt+YzslVPOn3Md2VBvDf3oiq7KYmkDCsYMHlCxMJZUgeA4mmFG9SzIaYFTuzOS5xTWVXi1hHnaRSSEDyvLfMmeEiXp8d6xSvfPsslG2do+f0+RqcjFdxvNXeXSQxmzmIaRVzDar6xm9F82LCdF880/OW+ndugw0IY5niJiPnIobwBiq60Bi7a+X6F3KfA+ydN+M4eOSFWh6goQ0lZWNTC62WD38fDr3kEFjBtriKTX+t9dC6sGvTC6bo3fn2TahmRsEzGtAa1HcRbVuWYSdbqHT5p6xaNJ9NSELr5pqL2Z800VOpMkhZNKjNCcLU9mlr5fTxBXHIbmVGnQNXXbNluZ/xorFenIXiMrH53FVV29nvaStL02yRWos21SVxEizL68KffmfnXvcWMUAYfkOtAhfeZYUSOR57KRSLONRUzBtettIoaYixq/1d9Qw2JOuTcpPy6VWUpNYlP5GqASRlyBqxk4x3VLWZeVTbLP26EdJpm51S4CdhCjVK+zP8lGqDsoWYT7TfPmEXo6dZbJFYbIDxdrepb4pyvC+M8aaCf7PgNNDn9F5djOXRvOZ2+ujtHwrPSewzDHa3Gs7QPs3okadUbwpEoOmHN2WvbKV0isez7uUIUbQ2VWcfYymR3AJAv0a9oh6bI38DEETxZs89XSsE8GK+2WM437lfSahacWoYI9IvlBan2WhUCEvLvOn4av7R4mm1OY1HkVsB7YQts96I8FGQ3oOimZwoaNpVWnbNZ6XGyRquq7QUrdDLcYgbqOaO/ZLgQuzu1Qu5pJK0GjwR4/Ett8RvUDtBhNYKzobgAbhU+GDxLocEwHR1RV5sPYqW6pKBLN1wJqTUR9T6ry7rabcTqtPi9Z5NLP3So21e5Degp0k7+x/H5DHUs64tkI8vFHHNCsnjpQP1aaqp02i6NfYbsvQ7uj3+8WepugOgmVMc4YcqkTCFYimQafQZ6mOtyktdJ9JJw+k8y31TxHxJQWSavT01tD5K/NvMjXE8fqVXrRnMFF19NkLBU+k65id3yfpqlHvDXXZBYs2wPVgtWgerT62rJGOLzEQWlUY5dG9qDUvNHM05fulE0lHmMgMSFlANjXKHHGm+HdRmNgI6bK+JhdBxqstXVrWOMax0DKnueeAZoLmvylvi/d2qaF3+MmcJ3rfQUvsloLCtv3l7qi721zj3zlwENrSeUS69RL6ybRWFEBNg82R2UyjnRrtXoZfWgGfRpvY+pm7ejNOkd6uVYNjH0OOz0O9l3osFgAlbhuEAV2G7l/K6KJihIVnL73PMnl6Pu77JdGfz+d77vGN6cIaPVkIDbpbhp2zk8jL1VhFcEHZi9rU/vIUgwqa3xY34Pfoc9AFDLw19xPWh6uLTTGEVrKqm0cWRhyntskHExYcAD1egTATcos5G1Fgax+mdKNCUaIfe97s973uz7VD3fnt9bT4t9VDqCnyzg0EiFgL44jKu7+YV+7QmvlkT2nlsCLkO1cfoxgJ9r5FZp0mwBKlU5Du4ra/cDqRyaMIagoVmUi8X1xyjwh01B4sRYy6QuReQBMZ0UayKmxw93mj33Pd32eV3PE2qu6AcDWSuUoste3Cu4e8btTDt1FNTExRcjXnlZPTkV+43oQnBpx5LhbXXfDipjfWJiQto5suAi7zAFbNxXiHy0loDMSiWpjwgXLiG2fHrgK66Y7Y13kmXbDlOXhtgCAX0vOl+21Vr/ApMBUqjfrlWTvcvesUb2HZVz6tVGdfLLmsA+sOJeqfL1tEunVx3kL6ixl5ZMsLHVVmbNZIFnSpuvZwvmU1tGvMXBsSaTcxQCzT1JJ5cZ1CgExdR5socsZHDttXF7sZdnu95mw932j//xAAtEAACAgIBAwMFAAMBAAMBAAABAgADBBESEBMhBSIxFCAjMkEkMDNCFSU0Q//aAAgBAQABBQL7MJ61bMdHs/0DqRqKsRZirwx19tdz9up/2qt41YCcehh9z/1Yf26f+jG+PUP+2/HKY7bst8WgyuEy5Q2JQPYJv/d/V+Yo9+tmtOTVV7s17jMx/c/khffUxBHhWbQq+N+5Y3/XkJ4M+GjGZOvqyZuYY/JkH84iOAGMX3Y9B8Tf+6pPCjzKk2VWYlW7cOr8pXRc8VduRiMBb6cOTS5/cDP69xW4ttyYpm/dsRpkn/IhZ1anJZICtzqikPWgL6iOErVypF4M7o/2Iuy2MO29XaxdaGpSv+NUNzF8SheNbzLfVZnzNamEONbXDur7rR4DERX3mLy582sZjZN6Y3anehsDXEzcbZC+2BjGAMNSz6RDj0KC2hOI/wBYErX8Nbs7Z3663c9WgRww6ddvFXcHiWeZktytM34/pyRTTVtKFPFLbQlDXf4/c/zHLtWp7avcY/mduL4RW94sm4vkkacTXgr4r81UdNf6wJQu8PDr22d+61x/+mT4x6fccT9TLX4yw9fgY1Jusu/bUs81MPaDq1b9gnlBV4sqQS5vIncM5xbJUzcrbG7yOWI+P5T8oNXD56/2pKu0/wC32AQCenpyrw69Llj/ACC3h/8AvmnVXp67GMnBCZltpbG+yrLelxkliLmeEbpyE4Uv+tHJ2rKqpvXbkAGjuSypVh1vcBlDE22nuXV6Ugzcp/6cf/sGXi/2cj9upWu3srC2YC8WpXg+WP8AIOy4/wCvqH6el7N0eZdu7t76nxHaU+aVUdupdz1A6pb4oc75SinjW/7I7WP9KSLMSNQ4miIljIUbwIGgbcqPvPj1W6kh9H/QJqVD3su78YaOvOR5tfazHf2Zh5W+lrwJljcZY3JxBNSzzGIWYi7wqE5VqgWeot5I2vwabEqF1rJVYDVienqOxqWKBLQssXzrorzcUyv9s7aZ6eoEj/5A/wCgCASpPca9Shfw/wAf98gyvxTZUbJjVcXfwudZxxuiiEy1+IA2uCP8PHXxM47v8zRBQbbtAz1BtmnOWmr6615zteNj2kPVZsjUI6K8Uys+fUE/y7wA33iAStdtTX+S4fhoH4//ADLj5HmnEx+5hgalx/F6k/mCbhhHKYtExF4Y9S6nxL25WfEA5PRUOYEvPNv/AFjrsVhROYmTeFDJyFia6hpW8ySO4SW/0ARVmOvvrr9x9wo/Rj7WOhkEcV+MAfgMt+MpueRB0+Z/MX32f+qfjJbhUx8xCOdI9t3tptOlSU2AQXrBd7VfnYzbjcoYeiGZL+UOx9wgEqX34/ybkQLksK8R+SvGMslFTWTEXjQZkW8QfJ+y1uK+mz+p4XPs/GflzpavMpHtzm1VkfA8QNKqvblPoY6AJWi7K1GW4tZluERHrKlTprLDZKuQm/uURVlH7XqyXU17Sgfjq0I/6co5np1H4UGleZ7/AG/21uTenf8AKvzN6Ga/K6WA6oEx19me27bfmus2tRiAM7dtX8tVbBa0W14HLR2Ev0Qw0d7VTOX2gRBFXzV7bcziDjH2Y7aVHhP4jDMNdVfxj4zv36mOdL/fTx+OpdC+ztq22PsEufZoEr9lNz87bPJwavy61Mizm7e5lsAP1Op9TuVZXGNclhYbjDXRGmz9qDyq6Ovbo880cqKPDCwrbzinlQ0+XxvFIlp4zMP5fscxf29OX2FtTPfVPIkfz9nxvMyreGNHr4pirzqvs4rHfQ+JyirubCze+hY6inR5D7BFEBlXujryx60NmNrgbhoq/KY5/Gx92PSrBBxRD7bztbz+bqTsWStdtieC/lsqzuWzwZ8th0bGa22DcJ5selO3RkNuw+S+lJOyom5rZ7eoRD9mvHQCKJWoZ+PaZT7tcVy69PxYikbbDO6iC1np9fPFgOjbLDu3qzaExk2z/jW23hVD5jvKVlZ7dDnk/EtKP+1rdrEc6hOoYBKq9xeG7NVwU84+E2rEKH7lEURAJ4YOzUvjN3KcmrnSfAp/bEMRuOVip24Yzae59Anpvox1Pk4g99rFha2zDPYDWsyLdLCrccKsmz1DI5Wajj3FSzY/pltktoO2VaZU/wCWkVZEtreqZKhh8faBFEUTHrGnrAmYvOn0638Z8zNQ12roHGPub98Z+VG9x4x5JC0ELzjqL5OGNS9u2u4T4LeEG2X2KxJnxNlyCMbG8s3xEr7luJQtc/mU4WOeRqrJZEdDVlHV+Mli3VFG6iCKIoiL4GtWV8GCvhZKHkmVV3aSNStuNr+D6bYGx96Zn2bQBUx8TcEYytZXuXW9xxDCyiY6dx8h+jamLVyfKs5vqctnHTS1IFXIyRL7JWw54llZhrBhpEUMhvqFq2V8W49BAIolSxQdHkp2rSyrklFistp8ZYj/ALO2zgLqWQt5ub8ZM30+Z7Ykts4oJvwqcpwHLxj1HzD8VVF3tYUVyxzrHTkyKRZkZnt5eLW5dEssqNPqGpVclgDLt6wRlJ54GagEAlSbZRyKnUdgIbkDBwwy1bFtqykyK7gCr+IP2wbuL2nwxlp9m+oizfbG9xYzTZ1SooRnLszalaNa3txKydsXAnmx8agVpkZPKCW2wncDRflqdKnKpqcnkO4RLytw4GagEAlftTHX22sAvllOJxld/bZ+F1ZqUOznV680lThWazlXvw/hCOhMETwGbkZszZlKBBZabGLcQnKx6lGNU7mx2+P2OLQtYuvawyyzU3s8fCUtY3bGHA+5zAinY5sk5C4bbogmoBF9o1uNtYL0IzKCZjWMJkDY7vcUEKbF9xnp9F90HpoEf0xGlno7avosxzF+WPibh+Ka5Y+5vULFzjIKktu7hJhbcprCCy7mY7anljThkin09sk9mrGSy3HrazKZoG3F+DuB+M+pm/NZ8r+yLNwv4fm0tssRxlWEm0FlyFYW6ptsZTF90xvT/qL60SlGti7YWDxkqmRR2jz4HhvUJ6VruPZNxjuUIBLbuU5wuTKkCyy3kQY1sG2lNc4ljzGPVfebSTsriswOPE2k8EOs2J/av2TUA8KNRvM1uZYHI8gX5ArbP+ktoXurUEtw0FGH/wDMg5Gtz1bOao4vqVlT2P5yvZkAflan2mrdZHBg25waGAQ2Gb6KoQFt9NjQTcWvxRVpbMmqqWWli9vKYtXJ60HFsdWNuLLK2pLbI6IfNR2R4UGBYw0Ml9uqHQqXu5KqgxUbfaWtsXGbJnq9xSlT+Sr49QbebMK0vVnjV1I5XX1cKq0JrvX3DxKm2WQdp69J0QQtym58wagfUFthhdjC+o7MemNc1VlFgsRl1P2FtS3V2g1WchNxfnHYAq3KLsvLj7DQzlh2YicMXI26YtXCu1wJ6cNYHrStzwcV77l8T1Opq8yemKTPVKCsoUEXDRA3ZkKBNeaF830ca3TgrDyqgh6ys+JuCchC3juGdyczOBM4NKvD4rATexx8suhn4810SVRPCIOjfAXbW1k2dnaDHaJSDg5NYqxsHJTldWlwycgYWPk5t1GMwT1HFf021GwsZasfLbfpmFMscEq/K2QPc6eal/Hb/wBnraWLp612ACKmX8eoa2CzfUa3Ti121vjPVO3Ky1ZTJ4xWDAeRYm1bFbluLMfy29wdH+ChSFjyOWVDXkJXl8a8q3vr2iXNuruaW3cKLoioBkeD9Z2hffdacJJanKvtipGRrW+m2Ur9uXTyx6lZq7V/JUmmrQMh2Qy+6mvuVWJpuomJk9srcjy6kFfkEkTGsKxXnIOvNZ/RMciJqL5afLmMI4We2Gqtota1WGkPWwdcmmwfWYrKLMJ+Wf6m3gYgK2UABMq0I2R7Wyead60P9e+q7Usp7idt1CUso7gT8hq1gHfZAmPX+C+oBj89BAdSqwyrJ1LCoj+BW3GV27CWcWIBP9WUymJGMTpk3CmuzIvy7GpzaZi5hafMxfNPHcNQMOJVPoxW9mHzL+yuurlFrAh4iErNLsgGDGKk25ax7LTD3xMaxu4Myn6TI4pTWVmB7sfI2C3z0EMU6KtyCPFPGa4kfHOdxp/RKZSIssiy67tTKdsy+mlMSrlPUKRRkYzc6cM766hWMstHJ1GgzhBkeoaJzLCa/UGErtW1R8H4YRxCvkBuPbbfArMbObHS25XhVCD8xVMNZA4xdiK3Kb3B+Sus+WfU5Gb885i+ZV8Q/KxotVFVrHcJnqCmyvHXt1YKaTqY8J3bymfkEDC9M+oX6fGSXemVXClnx7gfEaMIVipCsIjLududuN8iYqw1DRxI+O6CA7iHy3i3J/bcYwGYnxX0PwPiNCYT0rTuOihV6mWTfuhxmvyXZUXcDaPqtWracpQisHEYRpT5hEKwiET4j/K/OPRBU2iuoD4yMXx/Vl3mt231WYv60nfQ+Zx2O2ZZW2mBEMQF2op7a/YxjQDTL0J62BbUGPSIFAEaESqvjCIRGEImpYuiJj5HGVWhgUDCxCkD6mXWAysN8hxfqsx21McxRymgAW4wXxXVoVDR8FGlVC1CF9Q2WT6plg9QpJ7oI+ZfXximbh+3fRoo5N8AwwiETjLN7gMptImPlbnhhenbJYSxeDmyE7g9PuIla7KIa2x6yKl5TUtUmMtiGpWi/HRoutSwCZFayux6WqbmpXkLKu2pbU2SA3Xc3BOJaBeAJh6GETW5YNNNRSRKb5Vk6jEWpevBn8gzHUQ2szJXuYtHm/G7mQPEDGCf3xBo/bybHs76MLcgS28GVbY0JwSMuxdjbi49gYYiGDFQT6arbY1RjYdc7AUmH7dQCXYotllPaOugWI+pXdxmSy2Vk9O0zYv09U+iXt018WMq2XSCNGeV2E2D7LV5C0AR11K6y5opCQdD03qd7UOYBPrRDnLPrqmncVw0P3KPP6vbjiwClVZ8cdD4nPUFsc+euvaixoBxH9byEaCBR9pl9IcfSKClfGCbm+pHiwHTnyWjHfSpmVg/IfZvoG0RwtW3lUS6tBpksXYJ10P26g6GEdNald3IgwdRay2fMaETX2a67j01vLsWuwHDsnbcMlREA10PXc5Twy9wpDk+LOO67fJ94uWHx9w+erdeLLm/0Hqw3OLLO4RO8k79U+oqn1PKFMyyUIaa+lrEE5TCDLWBgQQD0MMMMJhM3DaVDZbNO7P3CyptHJE1tPtEYxTNwnoDOP5T8NZxiuD1InnoUSAKs5GHZ6bm4fItxTDsGhis5eIYYYYYY9gWGwmfPSs7nDjOWo9vOtD7nGm+wQ9P4WiHZMX9vmWjkKWKiu8Mobxv7dzc39t1IsC1aHUiERhGIEd9wgzURDGEU6KHdbGDo3ma+wdNdGgOoHifJ8Lx0OHGzemW7jEv5Tf+jUI6GETXV7EWPfxnfsaEEztnX9Sss+RpEqrZwuOlZsuhbzuf3XtVdk1GEa6eB0LTxHEs8SrcSE7e2ZVfg/t2ubL7ZU5ad0A7/wBGodQuIXXRyapZkEzySE93DR7e3ucpZaNxGChK121qcbrvO9rDBF1BxjPHHQmHyHKVg5VYnfr4fU8zVplWf+nHmxgbLAUtUDs9s7YaXuO5Nr8u/YsGUTBcrQ3agu2PqY2bqHLLx2YxmAmnacNBUMqqLFQAxbk1J5NmLPkBuI7hnMtHPu346bm5yM2Zs9G+cl2WN8Wxvml25Y596dD+zf8A6cn5xWLVH97/ANVUceI7z/8ANB+D/wDrv8S//mX9n/ZvEsJlYHGry1nzYNBf+EUTHH5Mknf9T4cSzwT8xPLEff8A/8QAKREAAgICAQQCAgICAwAAAAAAAAECEQMhEgQQEzEiQTJRICMwQhQzYf/aAAgBAwEBPwH/AAKHw5EYkUdJDjGzrP0iPsiVvs13h7JjI+v8HTY+UjJCmLGvCmTVGFcmLR1rpGOBD2OCKOJwGQWxx2S0Qv8AnjVnRR2ZIXNjj/XRJ2zpY/fbPBPcj2YsaJbZdD/Z5vQ52RY2SI/zxR2dG/lRkj/YSfxYtmFUhHUvQkuNkZfKkZlUiqLJrl6JKUTHOxvsv5R9kFR035DVtGWoxZhRFdurnvii6xHT7yHUdpkSTTHGjmIRX8YR2fR032VckjPP+xo6WNkRmTGrsy6idHH7MntE/dGbckhxFFIkiaIS2QK/hHG3sx4FdsnFU6OkRlycNknylZgjURHo58psy/o6eHGBO3kIfLIZ/wDtIRf2S0x2cL9mXFw2jF7svuourMO40Y4XjMeO0zpVVnVPRBWzH+IjPOomH02RjykekQdybMEfcicFdkUZMnzI5W3o8lGScZIjKmc+/T/kRgoejBlttEXxkLVmaV6ILZDt1Mvohj4wr9mGBkkkiqiVxiS2jJkUUSfJmHHo8aM8X/BGO07IOyV452QqUbJeiX5EEcqR5Elsk3OZX0KkiT5M+yTXorejNC0LFxZVQsjdHG1TMkXF13RBELRN8o2jpptaJPTGvkKFE5F7McLlyZz+VDdEb9i0hysbWONsjK1bIYrdyM2b5aI5ExSJwjlieN9ooWzHXpnF43/4RjXonISUtjWiTZz+R5OMCOSnZHI5sjJJWxZOez8dsySeVkYfs6jqOPxiVO7MSTWzhH6IqihEEVRHHy9ivjTFok09E8jxP4nln7kU5LQouycrIPloVQVItzlxXo8kYaHN5HSINLRkzf6xI9IvciGG3f0STf4GJSg/kT/aPOxEO2FkjySqjSVnD/ZjR08vlsf5jjFs/Bko6stw9FubOaS4ohsxqK9FfcjN1L/GJyuOiM2SerKXbGSdkJUhsejJ+IpckcWY4uLtn2xDjY0ZI6Iw0OLRycB539HknL7F06vZDDUaJQcTHL6Z4BEOydCaY9jpCgNNF3GjxtHChQkS7ekNWSjyXaJikpaI3EkjgUIxi9n2STWhcomf0KbI5BSstjnGPsjNS9FDxJih9FSORONEE2cGtow5LW+0tbPMu2P0I+xROJ1EvrsjGtHHRjx/ZKFO0Jp97JY4yOqxKHo6ZP2aGY2dTOo0c32xMcqPl9Eczj7H1CrRJuQsbYsUkQdd6KrukI6yqMOTiON7RCVk7htGfKpdrMehkMriZJcuyjy9GLFOzh8PkTezHk/ZLJFH/IQs6YnZFFds+JzWjxv0zFyRxvaMj+O+8URONi+PsyO+0JUzDnjxMuZyGhCp+xdPAfTxQoULu5UcY+xwXtEspkyt67pCIkUpXY12REsbQhRs4SQpsTF2bJZYx9nkT/ExybR1Mdj72JkcgnaIGTF+u6EhISIz/Y1YhEmZsrXoipTZB+OQ3xVozSsa334HBoboxt8SJCXIcItDgLuhMTFK+3EyK/RDFUdHCGOPKZlzuRy5CimZIKtFCQoaPFFsnHjrtHRbiY5aOMWeNHjRwSEklYlyFFIWzI6RxS2brR1GR+i7KYrN9v/EACkRAAICAgICAQQCAgMAAAAAAAABAhEDIRIxBBATICIyQUJRYXEUI8H/2gAIAQIBAT8B9cd39DY2OVGXISds8aNImv6M2jJ0R6EIw/kJElsojpk+/rbJ5lVHIyT7Mk/0QxfcRRPRlkLZLHSR8Z8TMUWmRJxtEYFQ/ZNxNfVldIlK8tIczuNkYcpHGvUqq2Sg5GPAkZYdChFbZjd9HxnA4jVDJ9+37bo8nJ9hj23ISpWNf9RhhUb9xin2ZEkyE/u4ncRx/shGo2QyJdipjhWxokiT2vpsyS0Zp2jDtFXEzSqKijG/t940eROpM8XcmyI4pMkm46HhkYtfsscCaHTSspfQ2eTlpH8aMUOMRdHHlsxP3zdGdW7PFhxtiLIdGRSZDF+yIicbQ4/aX7bJTPIin2ZKWkR6RN8YCdY7MS1fuSqJ5EqdGNUj+JGVyI/iSl/Q/wASWO2QySjoxz5In1RxfuciTJrlElj+6yJmqqO1xIKo+oq2eRLjGzG3lybET1E8ePchy0JHHR8SPijdkVQ1aK9NmRktsSFtEVs8jJWRGKOr9wR5k7+08fFx7EjyJapGONRol2RiLROQ5mOafuyTJsg03RLJWSmRIrZmi+dmN/b64i0iSTfpaJR5MQtuyLHk/ojszx5dGKbxy+8i01fpskzPkox5Kdnk1JWjxpcoCRr5GiCpUJFDeiMf36kxIZFWT10YVLuRGOjJgktondbPEzO6LHInIa/sfjr8kYL5cX0QxqHREzY6yckJCKKtlDVFD0JH4r1CFmiTf6Jq+z4uLs5Euicjk2yEm9IgpfsojobjLs/0RyU9loQ9HezrYo3sriU/2KJPNxIZJ5H/AINR7JNSWiP9M+NEloyxoT2Y40yMzVWORhXJWYzNDVn8RTdHYp7o7OihjseNSIY0jyVJMUmjx8vyf79NGYdJ2Y82yORE86SpH5x0YppLgiOtmSacdEpVjIT5RsjLQ3uzHIlITs7OJSR86ujN960NNIw5XCdnzIkZ+zIyKdpEcKFjiSy/EqRjlHtCVipK2ZXzjSMWKcdGTmuieSSmiE72SmrpkXRGe/eXx72K1pjVolhKZI8hkzG7yEWoK32Ql8mmhwt0fAhQcR+likxwlE/2RmZMcZu2KKqrIYpRm2RGy0ycRnC2fENWeV2dpmCk7ZEi6dkFbv0x9kWk7Z8sskv8GObvhIcWhDehMjMxyszOkLKyGW9MmjErKGeVAUHxdnj4oT7I4EvxFB/siiWRr9Hya+hDbfpv0mYWZIKaJYnDoWzHtUyEOJZOaiZZqQ5K6PHSTIKvUsix9jzRl16SGvXE4jf0Ysqg9nL+iaTJY66MXvnJrY+jlxkRlczFpeskFJUKHA7LJG7I+pL6GY5SSI5H0xRIxr3y3Rk6JGKPKzxvIa1IjKyySKYoMeiTEmcyT9qJHE5EcXEyRraMTtfQlskOFslDiR7I5pY9foWeLFkOZy9SjZCdEpFlkSEF+zSGrQvuIKhP2kh16mrRKr0LoljrojNrTFMUjkcizZ8chY0uzmkQZKW9kZzmyMKOhyohJ+u2LCmz/iqKJoj/AOkPubGrKNC9JbIrY3xPkZysnVGP8S9kF9X/xAA0EAABAwIEBQIEBQUBAQAAAAABAAIRECESIDFBAzBRYXEiMhNCgZFSYnKhsQQjM0CCNMH/2gAIAQEABj8Cyetejn4tzQmhbvkjojyG/prCdQ04hi4/1BQBBvdBuwFA2jWoMbqVFJTqMWmVv6KynUM0447KP9Bz+iNHHorr6KeiKJRJpPRYzQM60KYwboZQm/pp6QD5UlgR4nWnvA+q9zfuuLcadVIV7c6UB1NeIe6lP8IIrD1yBYAnOq0lFxVvaF0WtT2FYCiklaJ790bLTmvd4TW90wJo2RKaOpo77VPaoVvcsR9zkAndUOpQWEFRTWF71rKechnI5qd553FUx7SmBA91HVN8oNGgR80cTtksr6BMYKP7odAEHd6QLlerWkQrlRtUQE7YqFekLiDvmurZ+Iw7hPXgUhcL6qdyr0A6qMhgSF8UjsjbZYR4Tj2pgFIUu+yk27K+QJ7u+V7TuURl1zBYQiFxAnKE507BcFvZAbCp/LlgIN7p3hDzV20oAXJWM+5R838I4dBYL1SV7VpnFC/ZacoIrEp6pycU/smDo1QfcaHsj5rNO6nvTwmhQoCxG7kyPmWJ3vfW61zhOI7K/CX+LlBF1AneUQnnui/wFPQUJ3dmcU2p7K2qvThzeEGbNQaGyV0pK9qvk1o0i8tTcPTlAUK8ihRKA6lHrNCmcLplJV99FwxV3muLogegROWG+4r1ZuB+hX5QRNCOid4q1MoE45g7ZtXFFXUD20ce2SyJ2CLyJWhzcPs1TyRNDdQG/VElORoY2TKHxm8p1AsPXIEG9VFR1KHCb9UFdaL2r0q6lSUL8kFEAwDdOX/VHI0d3AQoeQKEdLZAsPSkBS7ZYvspNLBe3LHKwpjj0T4XFHQ0NR45EVKkoq5kqFdSiaSdAKRsFhVtBS5W6uCrFXHK8IP+VNITvCc3rT6UhN/TyJyAblRtSaQN6S4+rop7Su9IGubXl9kWbtWE0xBBOpwXRq6CgO1CjkgaUCIVl2FL6KAuyDBoFah8QvCgLqcuozTlgoEe0oO20Ksp6p3ajgoGqZ1a6aOFHecwQI2RcN6wKEor/wCoBSdSu+STooUC7l1KkFQRyZRY7QrC7ZCdQo3ainJyae6c0aTSUTnasA3WEaNpCtdBYOlOgUoMG1IVggXDCF8Phj6rWXLGbq9ivxNUt5MqdljGrf4X807FFOox3ahCf2yWUuoV3OXGdtKwp3Kk0hWbfrS31V1EKyw8RSyyvyYVvYVb2lBzdEeu2TD0q9w3z6x1Xatmq6wjQV7KNhklYGfekuREAZO/J6qHCJXdui9NMY+auJhsdVNDltTA3Xc1u6AobdR81LKF8Nuu6k1wx7VgYpXZWXpK9YUg0lqIIzQFB1V17pPRS1fG4eh1UfN0RaUQdlK1hSKOzTvl+I/XZTSAvzlSaguWFulIpFB1UtK9alpkL82XypXUrC/TqnE/RQ6yjYr0HC8L1LGKCUIvR2WcuPi67BTSFiOqkrWnxeJ9Au3SkUlYWiSvXB4uzei3pZS37KRYr25AKSdVMhQbLE1YUHt9zVMIjrWw9HUq7lrC9Dx4Kh7YrFdVjd9FFcbl2VqY+IraZMfEOFqk/wBvhbBQz0jqieGzG7q5bfTJbPYLQLZbLEPS9XsVM2K1Q/lOYfa3UoNYIApNHcN48FYViySdMmJ1YWJ1bU0WFXKk6KApwqygqynNKillAV1BTWi8oMbsPUiTpwx+6Dn6n1OKwBnoO9PgcIxGpUPONu8qW3CkeUR+ISnHopUFQFpSVFZOWUHOMBf2xJWJxUK11pCmsjkwEcAvuUcfqwhWHt/lDD7jYJsbi6n5S7EfCHCG+qB704s9aFrvl0Q8Lhd2q3ufYBFpFxYoHqKR+IJ53CDhWTl0XuV3U1oCFIUtpBRC0rMXUlRQq2qbwxoLon8Wqtu5cI9ZRDNGbpiB2hAx6RvR5Is6j1w+L8pEL+kP5SE8/gasX42ymU4XkoDd5TmXivbLbJqtFdSPqKysbRbNNSfsjvZN8L7rAfwqIR/pz8ui9bQ4d1/bYATpZcN499sS9Qgn9lFinR7lxAfxCFwB2XxR4d4XxIgRDQm+VouF+tMnTCY8qH39CKPhYuyFrik5u66haLsr6KRQtOhRtktkkfZFRh/dD90W4+HO0lBnoAOrsSdxb4RYHquFw/xBO4Lh7RN09pgxqFhZttQhl3dkPiWA0C4M7NTvCA2XDc1pchLYXCt86OH3C4TuI8yXBR2C/wCSuFOicXDcI+U7s5GNJywaY+HtTso2X8I5IGTxX1QtldoXtGA6rDsmcU3DWxZcZzgWy2Gyv6t0jUL+pIPyJoCHpWGT90GPY1zQrM4g8LCeLxo6YU13DGEN0XqYmOYJg3Wu266Q1DwER+Qr0+6JCLjq5d1xvK7ZrUxt0PuCnakKfvyi4qOGCewWIseFh4lAOlNEYYB4WPh+l3ZAvOKl1orNAFLCk8N0IiWu8o4uGVqU7E68QsDjD8MQUyCDK1Ep/dyv1z96YflOlMTdN1da5gKeppjqm8Ph3C+GzX5j1oHssHJpTh0zAUkr009V1Lc2sjoVpCkIsLZEym77lYsQrop2r3UKDqo6otPK+I1kOirIE3QBRPXMaYG6lfF4pjh/yobwmwp4XocsDuubtW4ppXYoiFYqYp3p5U5AhyY23QAzGl9EGN0Fqt4o+YIBxUtM5I5ALHwVcfanVvRfE4elZ52ECVfXmhvEaHAK3DarZCcprBydtwviM0KhEHl2V1qvSKdV/jXq4ZUaea4hzI5Oqh1JGig+05AbUAWF2oU9VrSy0V5y2yWMt6IFQVakjPYcg5e1O1XcV3tZ+5RJcb0aQN0HdUAFpyTu0qQ5e4K11G5UUuvSrq6spAhe1WkLXkyNaTkkK1eG1mGPc4yv/QxN7ICjjtotV7uTe1LDPotFpWQRyYKlseFDlLCodyBQZINNM1xydFGT08gLC7XYq/3C9Wqsj15AzSiMpbxBb5TzLturekoqC1acjCfoocsL24m9lLTSRqp52Eb5YIlegyOhXqaQtQveF7wv7fDe/wABWDeEO6LTxMZO+TVXVuVK9oy9nLuOaHdqXzXAX+Nv2VmNH0zks+ygjnQsVMP+g4Ixsted35NlehOwU0uorPMmrwmUj/Ru5WuoV1ZQVhCHCZtqtF67nooGXRaciMluqxJi8KFOyvy9QtZVifsvTplDVIQw3cVPF+yhgACtlvSJy3cJUF6Li5q9llIqPK+H1CHldynLoAuwQAppTSmi9iMSFdxpewrKlFCdlPQ0tzoBjJqvpk+iJ3TZKCcmWRtsimopyCKCtSaCpRNHVjmf/8QAKBABAAICAgICAgIDAQEBAAAAAQARITFBURBhcYEgkaGxwdHhMPDx/9oACAEBAAE/Ifw1N9zrj/xEqBmaXMsmUmQeifYqUhtJey7lPGWpiXtyxMeHxGTCCmMMHEIXg0uh/c1fEfCApPfj5PqY2ZhmMyr7R/kupf51KWhNg8SpcUvaxhdrUUzN0iQpAbQ9ywDrLFhIXsuZ/pZochtDcumbHtz4CjyOqYtG6lnDdxZUEssz4bFvhBzQi5iYHtbkt9UHP/qCJMw1gRbvcCJZaQ6PSBY8JmZX/uWLmGnwR1WVgBnmWuWQi80Wn6lguWfiYkjj2TmBZhi6lBLbiNnmWcwQ1xxWWpmCkaF2jOmBiq4R5g+mUD2ByhBmZ4XuoEfxMmqKnrf1/wCYWzHwog6bNzPsrDvMxIW7gAuZ99cx0xXDe8cpGNzi/c+s3FbDVr1A8bomQrrczHjdzt5mCmY4lgh/uY/F15qGat+YHKFifEz5lklLzDZgHLCELe5ULEwA0LJcAamLT9T1flUqV4rxVUtNJ2fBNR3NX2JRvDUDCYL/ALmzM9WKjARWqXzjAnymEXgO8w+O0YJZ98r3K03Mm3Tcuy8MM3pqY8r2xRtVRQhbLv8AyTNvONqtlzG+TUC8zPUGMlS2lFiVwJrw6Qh7QGfOvFeK81KmKGvkqZ9YsmfpwL5qZiLPUVIfCfMixYTwAFYEbLLja0TGNb3Li7g/2z6JbuZa1t+iGSVge0qa3EdMDM1xlAlaH8I2rQ9EFsFRa9+BbFftmeewlVJcte2Y6zdGGteBXkLEdiLqAHwlealj4R1yDArNkwRjQK4zLp6pcb3FSj5EReVzZMqUq/olrFw1Log8fLGNnhmDOhVoIl19pqLEGhXcp0oDNzZzHMZRMhfXKYjl9Hn5nAMRjCJuHcrDhmVcMZiXkcKjwJVlHoR/EEq1fhUIoHuKQxAsM4Z8rkZfrEXCVLbCSC9zYDuhWVRHgrcoHAqNmYTiKlyx/fCHdre4SjmM1w3JiO2VuvExRptFV0AENMt+eJUGCuYHj/AQusyVrSI6wsipOSobnFTK5elTRuZ5P6nMQz2P1+FeaghH7iWafSojRnaZU7nXepfccM9zOF1w1Eo8VseFsV7AmkMLalsCMIZj3yyS1HlJQVg0n8xhJDR8UPPZr1O3pjhslfUylZXMLFQBtLLNaRuMDWpmpmRiZo/3T5lJYcvzj89UDPgvl3zTLjmpem8j4FaQHYw9NWULxIe5R8x2MElywcXDU5HxfIx5tnysC5O5veMJle0N1t1HMlJ5DghiYgxAJwov5Wf0LMEsfiXaNM6Jk4imLgfKYd9xHUKpWihMv8xnyeGUrUqA5g49LHHwIu0D14qHthFvIN/EZDKoYA6WwguYFRYlxNRW7BmBjfIwB8xyYT7yx2jffHMGIztC8nbcG4EllPcwz/iolBgs4BiOH3GOPqWkxyKS11glfkGfBZ4b13cofJcw5DTwD5WOAbrMP65WXCQ7ismfKGIRUS5t6hVrJT0oEqlU0yr91XisLljmpT3Adw6NRerixZTbC8sdiyy7LA2xkj0ImB+qEcMq7gScytqUvASHMrxXipUOZnhYGILL7hqm60QTpQ+63xLFfUzek5S+DBtn1SYXPuZjtYb8bxNE+RhWfKOTXPisTsm6XDDaYaIZyzFgI6R9ETNEnXuFBLXMFcQFK3EXA+JYrv1FwEZXUuo0DXBKXASv4h4rtSir7iF4BoDJyxL4ulGKiZitYjfxUWyCY0RYlWDvHg8GCbo6NzS64hLUZvLBd+6jBWGoMd0Jkn6SYdF7KeKmzhBqjPCWvt7Zhv8AUcbIG9PuDa+oIyUzio1kKPMZo8TzXgzygMzPadnKQWxm4qTT++Usz3ZE5mr3KMdYYgmE7O3weoYionziOYya7g/vQl0BeInAXlZWf0xqPMdnCMscEfu2LHwTSUsPzKyFJnYh9spvpSpxFwWtKY8nuHf+eMahpslh4OJUIEFo68Zmk3lEq2TVwMoqNHe4YDsMQczSMbPzNfbEP1kVlzL9y4+ieoTRuUtrx/EZymi+4eVcwr+5ljkibahwRQy1C4MiAUbYYx7+WDiqcTVvGUW3bBFgtsbZfKZTedShQR7JaOIXlHfhMG5UqBB5sDvpTPhAnOKouvkaY4SSqc/zKlNhywMX08T7FGbfF4nt+p9wPmK2JM8DQgkbAtHpjiVbIDi4DEHEuc0vt4lhDuYHxVLMNYeAB2T0RLmZMy1UE5ETtAwWLPipnuX9UqB4tM1xi+tL6YJzH/6xGBqYsYNzNtC5aei58pTnmh2NmLnzJNqlxglxz8TEcxtywr3cQeg12cCLln6JZLIfM4tioZl1QcqYjzmG2DWQbZuFCy25Yyu6EK/iloqTjqa7XLTC0fwzBVKdw8cQIHkMamYH/UOKedl9dymLg+ZZUrMSx63CfUyoMBLJBHsJ9znGDvhnwhLlfcYWZcP3YO6K1cZnPr+MyBxR1UyKRKNn2xaru4Il9pfMev5eZSfG4mQVzMtywTRGeqndM52wmtN9IfZS0xqaHcqvswXPz8kv5fqNpPIQPIaYkIlwfn6j8XZrmLRgoxFPuTSKzEuOrJie5jae6QMMxDnk2R7mKRnETEtja2jRffqdeZT1MuY55SM9IBQm4gP/ANSiqrLBmFQjX4UbTZczSuY/U7lHU83LWsvhWm0Z36E0YmRMzBVkXZjyR6DMrwGIIfBekdNYIf7UC/LGnUUovi7JcC1qCQCmYW3plk3uDK9zsdSzDshWxKs7SivhjHMFxOaC1DoWvUXY0weCt9SmMxyyjaBzjiEzCLTbPRDbKA+mFCOAbmS5YZWMQVpnTG0v5mOhPcAC51C7qI0o+4nAxyR61F/epTuBB5hSr5nIxv4R/wBADK0MhlMqFmyKWMMIQKNvmaWU1wK2Cw6Y7suTfgYXiXPhcK2aiLB+4KqoXJPFaYTJTKDm9TIuW3EtuFh/MkB7cahoMRBeJoIAt4uexcswS/ctIYhF9JeEj4U+yVZs2HjVbUGZIeQURxKLi1KGE/vLAYe2FaEG7xzBu2wnGQjkq09MC9hR7NELDY8PMOrb3BDeGX5opZcXEXuazd76i0t5YqxEuguNISpWymYPEsTXEAwFCu/wR2fLOet6jimVmBMiPTKzazI2xHUWiLcLh9zlOo8QQOEwxlLpIjbqGPjWZKbjacxsIpoJija+VfM148o3Dtj2jUqQlf6BLEOTcEHvFMut+JBKdK3MkOpcFyrxtxHFm6I9jLgRqZ8s2C2X/MRpxxMpKIZuYJS4zTPKKwEqXR+6Vu64iZuAUOY5O5duh1SdSrbdoz82Pm/tmKczaL9QzlrmMrRb8xqWMxlvqjB6IWVf6Tnk61Kvq9kAch2Szea4i/7nTLqE2S2eIqsaZcbmFYgzLMss7QiXPELub6Ysyi8DROJTuaKis4+EV5QGTKBP0hI8zhDKrth/6iNxIz3HNZYkFBG32wS1HsWW1XI9xTMY5MB4EuZYa/yj3My9f3PB8OypNErYXKqJKWAPbG1GPEvWCcHMIgdfDA4ewmEv1agK6cMCbaULRUNLilVUUTqgsNTKRlpBC+hmT7VKqMg0y0YaqEw9H+Zjo/UBzLxU6WImmptmYFBdrwRMWCc0oxFm5mGAM/cpOrBHyV1g1FzDZI9YZ6iwmOptxQ08bvFGa+ZdBQ+xz6jp0T4iTtF6hy1pGTLcKe41XXcR/i49RgNiu4RCgtShPZRbMb8QY+iy38QStXZMBrCz4mRhGBomIE9Dc0CWo5GYO9xFxpIYuWI+0oZYj3l3OYfEf4w9xwNvqFk3UcwUcEEEHuWh7Nj+x8wMGpwH5Ru9Gxlf4YLj+ZyUgQgxu3EvLKfDAlbVwAzxLD53MQR2ycEZlYKyK5K7jEMDvtS4uqHOLyxTDYXbtOf5nR769NEUGv6pj2wS9F9RuQv4YC8BepWvWWmtk1ZdGiUC4Ome4Cyyl8nn+4thlE+JcjDiNzcEJIvUwIE0wWUVO4rmnxNkvyyhjc3OEx8zUByQjrY9/uJyRiOSDh/7G3/eMOGysdTMhQcIFFRBTbglZVLmDyNb21LG4cNtw9kr+sRMRVWfcv3ZvpbNZLYB51QbUS2BpUYFZY9+NBxiUgcz7lKyxH7mMRbQZT8h/wAIL3pF+5vgvwkfrGeg5iK4ERepQzpil9n1MdvtG/BdgHzE0EeUikwxeAbovXMO5LlSKDVZ6GAuJjjCoadz2xHNlxZjg4NwxhhGKk+I4KbS7c1kl4viNrGiQv2PcQjpcwsEir3KKc0C5nulEwIwmTQw+0yx5UppK93DF2DL2yqdP7FwbO0sw0UdxfRvpCYzm39zPuALDJtK3dEYDEwj1Frm1/uXE5xL5ntBTGzqp0FdRgyKsI1nP7QI1iaHcULcNW1uWssZX54MoCPgzaOGoIXgKDU3nEVLuJDL3CcDfxUoG6GP9pQV1WQTIp6TEcU7QSobKAx8pgi259YgNqg6WSqTebiOqbGnESsd3RqK8ukFBGtKjlgGdXgXaEXmW4Ootz9rImCxOFqH9cvSLV9QXFdtmC2WhKZkEW38E3cKJOIhQ/LC7ED8NpVaZbjT7jGj07g5eJiY2q3K8Xhg7ETvlw9QR37ZViDBGa4stQSW7HyYq0/SYO9xiVVsKFXUorY4ga3C5Ny78KjvudZqYF2YU/cce3uosVPZuKvp5QcOVdUz9wLWR6R0hYGCguWY1g8sqWtQzG8pvhhNfBT/ABEMjrusQUrtJvdD7x/yJY9BqWrViY+HfKIgEsVfxDSPwWoRFfUVZ3LAf/puAAZc0oFrTLHgtQsbM+5cLBGlTcgxfcoFg5dsSPh8RL1IYbWN3uK8ncSvcfaQnBl0IT3DGQQWNgq4TC5vM4CHEs3oTfYSpXwSdElSSLmOQiFr6IKnwFwQMvOGXV3NpctFTquEsQdKs1KFhGBiq2GITRaEqLlr16hzqPhQRYfGI+mCr/4EcN06iKbGB1HitlRFS2IEHEzSYIKPgl35LZpBP0csjpKNQcJ+ypiwg9qjh5nYEMHyv9yomYzvmJicKSoPFQ0P0l8uYs0lirijOj493i4cMFfIfCXQ8ktwNHYxWlktK5ZQCHTsmyVKEG9l1HrLtkAf/bmNiqav9xzpwSdlEbdzCaUVMN+4KPti0V3MrQYlKpyRxqLGvOD64QuE0ZiP7R+BxHRUNBxChLCf4o1m4g3P8ihGQ+nhjsKqiMwk6i3BZ482pzEUSuAaBiTuIvl6hp4rwVKwMVoHZEuVv4zN9M2uG5vfuUJ4hmKW7mSXwydsLz1MR420zMmYvBcrHvANUB4qVDiZ2QDX3LshvVtX6mMEKEbxrCB7MPsma1K7QdR8G0YHp+PZebKthshGjFynQzJlcIrJlHyOHbJyIY9yINTAPEZN8+N5hzGRYl3+4MK1B4Fgm4ZUWepsBnaWJKe5dw1LJcvwZqzYcrBZMhE5ly4mULLWaBfJf9yhYHREglrPWn8YY/ghXmmOmWTD7h3NzOCIXx3N02h84KuGKt3xDu7yvEUUVcvF6j0ojKvTNmpgFmBIIxYiUf7PA4Ar0Q11+zFV0/TLAV+lRwTGFoHOfMUuXLl+FxFcRBL+iUGPEebKXcyR0anPjNKm7f8AcRPNxU3tyw5Y3AfTEM8xN5Vw2XlhFM2tEelTZIAgMAodSn3CsbhXLMUjRL1vwwWVMHGMUNy44KlOTlUIHTCXQwKeL4DQFnqAm44Ll+OkyO/iXMn2Q+x78Cj5XFHM8MCbRWUNP6nFb5DLIZuOxynP2RQ1Ozuv0EuilbEydREC1zlZuhc2+qjDNvhizqpjKXecCvwYsC166mLJAX/OxRvfviBW2C+iV/gDAi7swhRD1CzK/UyrfhyMoyLsZwE+MTkfghfZRxxY+WKJZYqZjUrcvRTEC2ZMbjqnDFFmOSWtSuczeptFczsu+5ibzzOYYRVTBJZuBhFswzPgmBe5XwyulkWJx4SWpE0doeV7ZTEnGZ589IxovP1KubLl4A3Jj5ghFQ7dTKMfMWI5eIsWHgGjC9E8e41C3KIybPI6nCHpgUoUzsg9GZE4Zm14vFS/UeJuV551C4HUqSVt7g4Mx6olL1CtguHlIcR8WQzAwMAqGoUhN+EdIa1orRvqUEtTmWBV3GyRjqLFhFwBPOoLpX6EOdR41M3ezyQZm5qULYckWtRcxbPxjVQM3FKAITI1yQucPAvNFluPSdfMsGILmXyIQdRl4mRmN2XsYZwwmElwUWapwzJAfZMwxSjHFi+IKl6L26ggdE5l79kUqXwRj0LgOLbIYV53LKXhPxF/SO4QLYMw3NlQOWtr9S6BM0HwAQB4Y/vlZ/cf5jkx2lGj/LHLSfGYC0J+fgq2LidapeIs5YFRrH7R1GLLUhGbgIh4KKLyI+YwFY7g1NMzdRu+qSHLGs5IZk1WTMSF/jhco8JWXMWvmZoh54icrN+le4Rhgzfhrgyux8kTubJfGR10RbHw4RitSYj1RF/UYlhx1CwixRx+LmE5TMS3hnSBTU3m42UMc+o7ZQ7o3PpMsj8VZBcCpcVMDPKXjU7JWzB9XL8ZgpeUBsP4sRBHxLHws1KuLKKymaJmVjzFO5n7il5TfglBE4HEysBXSbzFQ11DmHHsTSV50lRQR1DUvS3m7hWwqB90pW7ZlmswpeGZwUW6hMWGFosWLHxUrEfAr8EoJZMEFwVZBLKMHxHFjIR8RXqcymVstJZu7YqCwywfGal2oNUTIO5rAikIQWmXnHXjgCWBmCxsTJG0HMAJwmA4lqDak1W9Mo07qo3M0b13EYZfDB5jWftKOmX4fPETxYheL7lkmLgjrL17IwjqGLCNzJoqYl8wsOCYHNuVgpZYu5fyhKw9YIlv5TM7gyww803M2kJNlxqdbF3xKhmISAX7BitAjWABu9wdlMu8xE+wYcTUW/GZY/q+YzJVQIvtmTr1EMMDEdhIi1f4iUbs5xiAXRJeU56mfdIV+pQw/e4Of9oAmHUbvO9zS5ZyEFdfUUWxhwI0fGCPS3vwsvUlRbA/c0WvcbLyxxFxL1OGDXi3ct3PZPdMVX5K5Yd1OTntmrElRxMRerjVOHwO5o+oMXm0b1RMkVMGLuGqOpReWZ8IgwAUMwwXFRTc9xZOY1vmQOpk4TvTQMw7cw4YAAVDWMVv4QrozULjzKXeLYusIjHMLFCoLK8hAGELR5Nznz//2gAMAwEAAgADAAAAEP3Q9W+/a1oXvqgONRC8kuNZbvu9429cO595AIPJ1Rg47ZdCJv8ACCFdGTmYtcIkxvlsetAkyMsvz/V6HA5ZOCevyZu6W+GHgmtPEAyh791DwBxAiE7i52sj4VqAgfjJz02pSsSf81+lp4ZYvn0ZfrA47clLuD3jcjD3bU+x/vBxdJe9MCPszQRogP8A6n44GtKhoP4ZT2O/RnqNqOmXt5azn/Mo68TvZwOqPOQV7UDb3UNTwFpQI0mbNm3iADPESSv8BNs944H9F1FN0p2pCLNys6rUSVf6jCmiv0LsUouAAGNAOvAvYUtizTvoKkPpj8TgTJfBNZJqtrb7pxqBBytkxHbrUX7vPNU2TB3tu2J193rDWC51m7vgE+AjKhfE425K+vbsLACQqdb6cTbABie3fzrhSyusQxL9Ljq2JpgGwndyzgMEmdBk9zqXW8+eTnD+n98vsYK6yPJv3TI8ruIYecPkKwP+IfSUbZ11q8A/XbyE+Ec0Nb5wn7k5kSjhFYMGdN7glEmLAtveOf55ljcT7KIp7aM58jUmxZlQ6Pf8d0e551JkpP1+kn94ItpvQ+OUnjStZvRa8inGlrFFQktINejzKp22LAm+LOJ3dZDMWjEY3kZSP//EACERAQEBAQEBAQEBAQADAQAAAAEAESExQRBRYSBxgZGx/9oACAEDAQE/EP8AoFcJMiNPrf0/ANXrcf79YeCKqWihztyLMywn3l9XZk53/rN5dV+WmWueEJ5IJcsINT15Idb0yA9/kb4SECWZsQ5fBMwuo427/wBCmy6+2Of7Bn5JMbpN5DnkRii9/wBnpsGbDUhAmZArNu2w3Yc/422OoTDlNrAfyXHeE9bZ63fY8ixeEmKwQ+yDrbzXyQRDUg4uUuz5aW2/p0W137aEzuYAv2ZQsA/AftjLa2YYiHb3qXk2D7sDjaNI+GUbP/GTQXRHWKsd+HbRv8/C5kLX2eIWi3KTKsiwZl6FszEphkLn/EjCi1cbKCV2Fo9J1/pjBuLfTLMeS3BFo/ZDPkOX8t9Htm1R4t05IOC3St0sfrsIGX7/APpdy7C1m34/E5EPtp/lsO/YPXwl/wDk2Sn2U2xZrGJ3bFGGe9ZZpj/w4n4TR9ux5v5KzIHjLv8A23/4sd3gh1izMH9k7a/LNPkLl6xBYf62Sl58ssbm3dN2AcJ37bZC5KM98hgTAft7wVLGmyK7cObycZHIBDsY6/kjr28D4sULrNjAdisL2dJWoH4Q7Y+yXTyAA6e3Y+XEY9/7cCXWC9MsjoTNga3Z+mDpItTrfYE3978CbgcL0TGUuR9L/KLtt8o7/HQLfF4bHh9iKBdnUBy9j0TjL+SJeHnyDD7QUfC0x+Ijp2Aw+2ep5KBZ9/Pr8x+Ih/Vl6r5Mx1y6F1uOl053khWskL7K6RxcOvLXPP7PYgevbRtrauuLYEX2A/sUPzMr2YnJU6yLpFT29F23QgJ9W6d+W+Jwv5MIHA8tMGS59RgR5CTQ5wlMGsnVOfy3eBAPOEAk5eT/AGh7+eS38tQsrWPgkA+krBCkdmfL2ReWoyC+FJjk/qy2gx3X2/tScvXyZ/1evy/z8IvSQMSPvICkYv8AMhCD5HF7bODeg8tcbiZJ0LBlxX5Jil6us9hx+Rs/Z+B2PIbEXJBB9tGrpfWBK8ZzPgXrO3vLDy7WyBXXQ5J1+Wjd9lOSv7T5+4zwsHX45+fLZs2de2UxhwNs+28dLIPRD4X7DxGNXQSCGOWbqH0tfbe/A8tjIFljNnCEv+8xt40hqXkkg5JfYPiJ6/o0POyvJBXgZ4wfh7YzpycD7CZmyrpE5z1M8ZZIwWRPPwP8y+VfH+rPw4BQvn6SZHoj1bG63G/hh4NhfDIukXQfbkFrDIpkcXiWvn6b/wBD8ICXPIX8dsTb1PTsBA/JMgM0ORr2B9tLaMI69j+yv438OHMbOzIDRLf3x+GDbjAXGU7MT8HIfh+HTk+ZA6IZKEuGbpO3PYfkMyFn1kmfgmQSOVtt+RY23h7KMI/y7K6WJB4jXyznYEnxD/Yz7gkhhwtLGc2fr1at4/XY6hAMQ9u4H2GsHSWnMtRyMrNv4ho75L8LvdAhe+7AtPL2nbSkvste3/nZf//EAB8RAQEBAQADAQEBAQEAAAAAAAEAESEQMUFRYXEgkf/aAAgBAgEBPxDwQzx6sDfBsy5s7v7dv9h3+pACwjIj1cvirr205i8D/be9s/6INbAH1n7lVfkya+2v8WJhYw3uW2siIfkL1sEcl6nqae4dDjYPWOWrZiW/nxvnbqRh8LVM+Trr9kPfkFYQRH4Ls/sYb726oPUhhFzDG/2WEpcvWb5luvJXxtmWN4YMhopwpYC9sFlog5ZLLbKzWLNiIOS2Kz8Zli3ZgbHR9haftssswBR7HqRqSMXxI2BM2Jr4wtm9Uuos+YTq5M4hr3fYnyzov5zLLZ20Rj+3uzX9uNtr2/bZSfGGPHF0fbkcnbcbmeTiqacWXIYQDbmWwLtkJrtGHYtPoXHQn9PBexsW5tgK3Qs+0S5C+k2izmG9nA9HiWWwMu+x7WA/V7ZLF/YHJIAz4gd3yEPpD5Zr3H1kMk27dYkTW2wMl9POdsi+tsEsjsDF+XYTAiyr0T6vtLx+yHYyz0zJ8LSGLDuWJry9Gz4ZxjzvgQy4fL008HY9sgQkG3TyBGjSCCL2EMNvYWLtvyJXfUBxY2M/9WKWeR+KTV6sgt/tiD8um2JdjC5Tgs8F9Ed9wZh4PwScFsM6/tDyyGuyKBdT5HPImMIxRzf/AHDSQ47QMvSX09TzhEbtjnPto3ITXW0azxatmfRAw2/231YXAXxYThujIY1hMgdjZVYh+T9mBepAa9yPVgd92nZ9mActO8g+Lhl8CjmSAAsXIj3dYSh15CjiakLhLgf5DLcIshsRndgLT19wkic1jdtj8uqMOz4tfywIAx0IXTJF2Gp9k4fVsDs97kAvd1H5Fl9Rg2+p6uiMowwCB+l+Dxmey7zxMZ+48vp+TWA/YB3tixITLS2v+1mO/NgaCXje4cuQOyQmZMMkIexuxYh4x6mJJ9x516uwVj9b1iNjuTElnTVAEA/y7OPnGcYq43dwjdu4zi6NiOBBPhF9hnB0fUt5AHbJB8hnWOK/xAJagno/LUSe93Z8kiVckZdz5JhRXB6newPqUdJ+YqGTJ2Po5E9NqnQ5bh/PI3UjNCNoUOzA8S69J67MYGS7pe0tnzIfHsuWAZzZnwho2xCLGk3btitj6PCm+kR4crvDrkO0dsrd8DPT6gJvpD4zKbSXmWk5CnAaJsIo5sfrbatEshV2M3RyATX7ZpZtnn37YDdJzAPuFaWeVr0tXMXpdWgGyt5avq/ImPYHBdci9hFo+AtC/wAaGnBx2PPvXrkOFpUYKV9TQuwHRl/Y39lP22KJw2knw7nEceXqrfD8hGEFu+Ae5v0zi8iDf2eJ6HLtidvY9vDmhbEVq/RA/UM4x8OkmzX7Ph9CZBwiMmJ/iZ7tJWs8w67t3yGZsZE1tg1Y1zIBuXzYeGFwQDhcITb0C2k/JHCbH7LMIRsLlt//xAAnEAEAAgICAgEFAQEBAQEAAAABABEhMUFRYXGBEJGhscHR4fDxIP/aAAgBAQABPxDj6M5rzAZgRzpcd0PMlfQnE4ZU4gEshCNKvOJg0y3G2/UqCsXbKUKNPE7goNftnVmHt1LFVTb7l5l1LioyeZWSy/JmK1ZiG1sHLxGOHJi/vCtfUJTe8nmHDKnrUbkcsbrMs1urQiQbrEG90mfczTIjEwjc8kwRXnwH5TM8wHWMdCyMN6Wky1PScfSowfKZNzmV9beID9AEdroheSVQsRKjBmCwc6hp4Q+8J63o4dwnhex4/wBicNlueLhXzMH26lDbG0HkVCzhGNGRXM8SkNi4bQPpSXqaIY44T9o03gcnMKqDGmYI4nct28zAXnMNKA3pPMYUNRsxiWqlhXqoiWQ3eivdSuFQM5TsuXFt3BK/K57/AFqJ9KuEdyn6O6j1/sULBmAHCnlmCcCuZ8wE0APfMrG2TW4KKquvUa7YDT2modrlR6I41Gb7TPwS+oyvb8QxWLXlga5tMRxhBpi2U4EQBjEWdRS47jdhrvB/WXtLv+oNi0HmIkYKgWme04x33L8ES4vPuF8xI0vMoDKkUoZ1UeGbsWXDUMEjhS5o8ZGLcTEUesvJwYbYR7M234ha2jQX9UcfRLiYhOZzOGMqPEI1p7gsq0uY1ieyoBsRY7EDEHR8WH+zjRdH2jqMWH2hFoAsvmWpcWy41NgdTaVGs2ag8yLyhDDdkp0lRa9427o+s5jA4DaviBcDT4InKaLdBqYTypZ4loJKs+1NL16M+pdIbhOrPghAigZphvYZizPs9TK4NAhDEriaMvUFR2MxqWHog/3cx1UxDDF8NxalPofSVKlfQJSyUzNmVv6GbahU5SKtZiu0BcIHA541Qf8A2UDGL93/ALMdERHJ1OwDA2OVwk3q383iOntkfMIGqDExrljBNl/tEWoHuGCBfbEtBaPSH3BAZZdStMqhULDL5f8AsoXYvDZMYsZn1bGBXW7Hgr6ozXNSv4DBdQAUeiJlkedJYiUcDmKLQ2Vp4jtsaPUQiStsV4ihmVwcxq4DuFGZ2AGI0tcEb6rJ+IMaK5epbTzAVKK+ipZ0MrMAQKZX0EVV7lWrRF+5TUEu9p/wjrd5teWXrgVdqYBO8Pi+5hWuPCqJbT629socKYYYHAynBie3REIG1VWIVoo6J2nta1BecuuAmItv9SyqM1DolFFKq7eGXOYm9A0H4mBkwr7rMV81smSS3KYjRTcuiY5NutRUI+CUJHSUg0EvduVg2aJQyGMF31L0Y0FDcJXAQTNQAMuzENYGnGoK9UeXkSmM/TQfMGEt1KJRCAtCxhu1rDvU4+iiYhaKJKTPUEgPyIVr0k+WPWGD+wg1C3yhdOHo4GpU7j7FVTIlpHtA/wCy51p/uVLGIKrd9yvvLIaNsLGCrlsRqOJ4nEWBaqYcIKMDuHoLovx/2EBxmOVuY80TzxH5TAm5wnoSp36PJnIhcXthbY0ZXxANkW/aDtAcQDD14iodzMQ1xuDrqh9BlgAEvnrxA0qqVmCxeyoNb6inIY3GQMHkgCtlJ6lH0qBSSny6TmBNNQu5Ydw0NIH7xCQKwxMEQR3u/wByiF3HncBt4AigFBVwMwYlnZN4Ak9sBxtjq6iadUzIZ2pJfahDffMV2NfiEWqNHMZcAto5YiqAHYC8xBFGRPiAOlXggZOTK7CAAWC4IBWC5oiwpsAIyxkQkDaqtA5mO4aNO3zDniDqGipMVMiKIwEpOtzcAiXzAIqY+yIdy4zBY3cuNLu+ENSV6Dd8/RVE4lfQErJNpbxL3Uod6/uG1omOPXXI6ggNC3o/+QKC3GZsKBt08TlHuubOpQ9BVfNv9grWR2m4GkxnWJmMjeCXPNp3Ml/Qp5jUpYaYiNm3qOp5lysQXyr87/sdBoUCNYbKb+bqZl2wpeHnzHwGqzFL6WPeW4v9AV2bMfeF7hmCGAaIsCUcy60vqVRFvUvdTHtriDySGSrjCh2rikqYCA34D/ILM0sM7emKNot6T/JUrECBXmVeoZH1XawfiCKsgndwL7TWa+/JmLfpJd7tfGYsBs4gMFI7iBaOR2BDGgLHgGZXuzUxKgY6CNk2zG3EJDQS3AwHDKKIwMpm2MKm2j7wzzVNRKKRtwBTqoFAUCgRnutwk1VTEDb93HmONRprt3OdGDjM4WjwQGurHty0vyg72GL2iK0uymEtlfRLTKJdrBKhXJtDpVlBT3GSS/4bgQCOgriYYtjqGWVUrUDMC2YUuZjqxcwUsF1KWZVkqDSA/wBgtvlb6xL1XarEm0Kz3L3Nu/IExSHH5FQ3aQuXO80stdOt7jviXKrEpQlaWKJUFBL8URN3ZV1H6Ilm/LLibEYhcZlCap+IoFLYOpZG0wuFFuoHmZhasfjMTdisx7aoHFSigzLhRZVQSjiYOOAdxbWYu6qKExOmpdLK7MuK8eI/u7Pc2nGmKfHkvcQvoHgOJeViGPoSsjLoyExMXcGyvEIdQIDQiuk1uAR6b1c5LSx8RnpywE/0TExhsX7h1Ow+ZjrX/YKIBSyt1ljOthTwmF/TGxHbwhI5HWOIRjSFLUQAAGscSyryR1WFHtiYnN5YYiD2FssVY7GV8xZKC3FNxfVd6j2m0JeicyrOeiJrgFUIqxcE8TMisBqYYXzC6tO9MsIae5evHiXkx7S04jtDYDcZywH0cahhAyTaEX/KMjE38tmDTUjHwxax12MLWjctfaF4CdgqJb8GMETgte41otq7gDb6WXABVY18wgXUaxs2NcR1XK2wnpDmN0G3fqNGaJSV9ziXxtEfqO4FoQL6yEDIbRTwRjR3B5qqiK3my4dDVEZqjC8RX56Yl3L+SDqoVuNExsCqdeCboDUy7XuGlEcky6HkVAKFu0CCOEiZoVgzB1GCVlpwPUKOYGJWCBklS4iqRFQzWIdEDX9QIl0prcsgFVF2ykuKP3h7BxOG5kE0S9Y2uGBdc/uXdb1vmaAgDxAvxcEkl0TxDDeMz57tiiIGZP6iN6B4hcD8gzCurIFHjHmCpseW+46vOWWpKc28y5UId9zLreEMEs/eDQBp7lYeazLAXBSoE4BXm4l3gK292yo8FoVogwWEU1h85atu2Y6OU3G4oo2PMWArO4OqQ2yu19Qx2wYlQIW+gqcTB27Ih7WZfUGWL79VqCwgWLh+gaL5ZlGthffNw8r/AOErW3bCJO2nqFSt694IaAeCIC7qHJYJAz0dxWUIKYgbMsMrZVssuc/yVEP/AAikmVh7m1Ta+D8xCnaDNe4JMQsLD2wEMXoIHiAX1LbUXyw/kOrjY7znce63qFCygz1DXqlUPPmOBOAe2Xrq/gOYzKsCcr5mENvcfyn6gpYfBGlgN2q/Metp1kTXE8k5y41F5OJ4WBlCkGZdC9tsSuHJ33F7BA9c/iM1AIb2G7lsGZG49DMfGIyu1wXyNj8EuB5H5gD10spfnN3N7hGHBFSvH7SrtVY+4toNXmDDLLHDiIKwC1YuMC6JnsCLiGkA0GVAQtghbK2zmiIl6WD7xUrDcS0XnErSot9r46IvGTRTogr9lXCtdkNh5lwhqHlolkEye3uXWvMJPLXgjTSqKdRr30mM3uWkqTPHjzFAxJfKVF6uFDCEHgfSyErRqMAVaORiH/oMRBXIit7sl7bWN9kAsSKchtMvWYpZeC5aGhTesStjQK/mb4/L2FV9oYmBCCo6xKpzgS9lo1AB8wpaFpg9tExtRbLtQGdBomMMDcf9YFZle4NeoyLf6MQHogNNKd7lIEvljFKpuJJZVvmKCBlBXTwRVSqKtvMooBIjztnD7r/YnILzG5LdaEU7GYrAxABAYC2xsFPHmHTNYxKHV1LuA4Z/4uHEUaYbfQRrE3JeLLTyM5svp6omOEez/wAIMcO1HEwcxidzFQtA8uqiKyD0gsOR36qOwtUC+sxLw/QpQSviFnLFjxH8qrE2uQfeZXfE7OjiJzcduWFWzBSjLK0FIgRMS/JUECjt75liOVbXtisF0dsBOmGOpdBuK7sUPmZwG3Ma5jMiggWAjBCZxg5a8Ri1tVrRH6tsupu3UzFYg4lyTUNrUEbWoGvaAbOJyHxE1Cc9VFi0c8PzLihiYJmXAVZw8TDBsxDUvuDipfRJcVCpHGKa4PuLFxLy9fxK3Ks+lYm0mtrNSzcPPTAWhch0eX9QVqCI821MElgeBcxAV3ANirQYvuJsEcwdSpYqE8wqBvuKRrcMTEVvRa6h9qreiHc9VvTuAPEAOF5fmG6MHM2Cjl6g/wCGBcuALkJjBGqcsclO9xEabVq+BN9ytk54jqgo9oecvMprXPqZWBoC79QTB9j8A4mPQM2AeWN2bDgvwQROTH9TPYBgNIy4X6JBhdDnr8cRAGjqWrLmAmOXpBliICqjjuaz0dfuJuTnslMXf8gUgAqbp4ZXb0gjEbb7k5mZbUkMvlhgcqqSoNP84sKhuwshPJPyEv8A5JXmaXLlxHc3AJUry6gLYPGcABwQixbTMN3bZ4HiJDaWy0XlFYZeY5tNkdHQKHff4/sVg23dxtcfcpY04Cawhlq12xpxWyysirag4WAth/NVjtfXUwEynrMBTMpaXomqO/ZBQVs4lgYGkaZhjiLTXvuFOKUfD7iZQbxhihrmW/SWEHqaMTWMMIbiECEqB5Q+wt4jcP3/AHF9O10jBrVCOTxKtjycvRK9TaGuoCtAa7jEAKnMdpplnuKGf2ERWrP5hEgqExhywQu3MRG3BKle3XiXILe2WZngxKQCoGghM3DkeCHI4+0BrThK6Xcm/iK1HsUDlFh6hR3/ANm9CCX1sJxL94qHEIrrGWZdu1EI2Xgvm2CeKix3og/ISiu9GDqYgPRpFQmyKv3FgFOSifHRh4K/KMKpANlZIwBUNzFpNMSI1UVxmFWbg6hK8RMQ4Ewx0uTVJ/8ABl7C8bkNj8QeixW6TipV6vNPEGcK6FUdkCCcXELlS4lwxJzQE4Kw5PMcsti7mbLS1JavWCUFvPmbXHQAN3ChFm1zGIJdYICQosHfiZpnE82g1BLbLX1EcUhfbLKIAs74D1G5KrawSF8wcLXpmovZXkfqOSlrmCQKPLKeqmoKsWOVYWw7L0HUWwBS1QPKB7luBBqECq2OR+JX1muBgFxV0TQj5lqDvEsYbJZEkZ3KjUvqVtfyJU+TDwgpY4e5VmDBbQO4AEmsQw+KtIbGF2sbHIx+UvBoekixtLKP0xW6HdHoYNFVH/YGdgsvmMi15TH/AHMU4MB/EWB1nqLsu4wvXiJWjB1NSwhNuTK1azEKBTQ6IzLbGADZi7sHMtSF4YgN2+D47jpXoepSS76JZF2+IMulimfbMmyvPEJXA1SIRKKAlHZm03FC4KW6uArS3iAkoODmXVWuItDQcws4NQre9RI1mZr/ALDDctHMW6wZSZXjNXiIqKGnmARXfU6jMmoBwQVgsofEAANrnqbs4rMEDaVMnX+pi6xNerUs2DDwY6dMvzwy1Tf4PmVVVV0fMC21V81j78zg6R0bS21EIUsGc5rkmw1xFZDDy94gNPhFCh3DUeg7YgZ8QqO7iKlfDUMVDxKpVBpvfh4jhkuEuaNurnOgquI3W4svljzoXnqIsq8EXl8sUq7HPk+JoJFaATK1TOSbzNYt5nEA81R6PMXqxRlLkKZFO3k8S02G7sLlUQi8QrCHRlzXN8Ca/hDhgEAo5e4IquBIoa3GqaAe4JZQ+7FzB5It2q8ocPc6btkD5IKuKzKRqyNrS9sy118y2sFxn/IOKNpcXO77FQUC7KuZqi70fBzL9H6qCk1j5lmhYFX8wC62Mj6ZY53DSLRzNWQhhLxCzgw2iqwqyxu5e2IwkMr3AW/wdzcXgI8rD5GIc0XBLWMd9TMRepuoaf8ASVlU4PMLZoHOIjSngxLajT0XBY0WNl4OIH3S2lq64uBRANgV3mK1jayl9nMt10ACI7mY4WV0GEpBBk5ZZY7beerMnq6hNZkPJKFaqCKsGWo1/vaVE053zfaH9XQDUWjktQ6YaBZo/BOLvpr2PmWihY3RyMqaW4tjMhDipcJGRvHo9wCowBwShStdx9g4XG06s0w8yqtlrP8AIKkpEl8QYcVo2dX7lDJfuLmpEXrMwjWk5jY6oqmg6I9VxSYAURTZmp5Y4iouA1KiVb4huseCBQ5IUXE1mXCmEdz2RNWu/wCQ7xwWtbg2azYuvB5i8qSg7YpCjHEjtl3UYmhtAzAJamwUxZQ3yiIBmuuoy22bjZm79TJfMYHuWBcCPcahVgXWZRFsso4RUjGZTghwixLXll56PYlAba6PEpQAYo34emZUipo0/KOzYWGnV+QBflZYEPxWags2Dtrn5xUEC3dm81xAJV3md7xEPAeuWU4DDIDhR/kIqTOu1HlVUDxc1HWjxKhAyL5L4lqFZTHTMJO44C6h0RPc1ExjcQpmKb6rUTQq8RzItiFgRnMDkTbO2ibZVAnKBQIQYdD7srpRnC/iAlK+I9R0Su8sRy6rViPaKm8qv5iUoFApJRHJkNMtyZ4puW5DHNGGUhnIhWORO51TM2vM8QxqsrALAZxxLgMaeY2d7LuBTUeH9zIyugxXmBVCX1i1R58S86wAayot8Xnth/h4lOGD8ZiEmAa9hnmsRw9pLDry5ap8Rws7RrT8rKORWBppxFEMoJ7IlYKn5RLTQN8QUccxclyHCvHwkoLX+0RaiLW6xLwwMLXnLUB4imw7lOdb7bzr+SgRRNVFAK4FUd/2F8Hp5tSfkl0S1jddSlzLcNxlkDR3OYwGo4jO0x2tQb8sUFTDkfaFGoOAAHxHVT82ZabfCWIR7QLYbS2tv2XHWEM13WSWp3lHD66llIpO5RQBp5ieAHbqFJc1zFFxs+Iq4hV0RrVVE9R21b/eFhYIX9lgmIhue/RFqA5C8Q35ti1a1q5KQz/7MbKz4vgH2Xce5STgowLGKwyNiLD1VfMHFjtTklFR0b7jrbVFDXBMBaVxCuE8YeGHmKDLdnnP+xrGJWyDOfcPeKXfkywDrvnK/f8AUUIBUHdq/RCHh44IJVKyjzL8MKX2NR0A1HlWf/OpWQC2lvh+zEXHRGcZCXotXCUNBYOSfD7gayZli7o6iVGfKCLYls4JZchsWN1r1KWWLzhQpi8TTTJuJxNAfc8MwURIC54XUEHxHuV3gXHEYLpjd+gJRPmUiyJ04ojUAjsS8faVLyUHrP7iMiBLHnH6ic7HBP8AF3B1VsfmExeKaULyPEMUGGFXbll/nBkBRgmUcKGCSxqwhy+eoJbCC7xaeI3/AAa+B4hJJpSv3IFK6/8ARiagwvtqWvgZascJBtuoO219owEEEdCr92GIKFImy0Moy82FS4wqejLVbBExkv8AkIc3m5qnEuGmWfUObPyiorIBUF2cURcrKqlPzMXRXWIKoNwR6mL0wLCzaKsVMqYq2CMONja+I+b87VJ8QVqurYRsp+Jl5gKbII3gJmWenRmSoEL4YOW2l15iOcULZsRSW9EDXjEQBTAQzd6iGNij3DM2yLzUFrkZBUqyVwMiDZ5EX2Mt1Stv4mRKESO3ZKjlXildB/Y8G4SChpxmojIaceFr/kr1/Uhe67lSBXY9HxcCugLsn1uIyXnHGYK9bsblWQ8qOa7e4IYgquVsgXiwxm8YgP0P9CxXPdHOT3BLzgSpCLh6uCxEqtjsfJExMEOA1FYAbpaWcTe7hLzUu+hKSwUSYLWre4mHRfuAW2inhMxgyCnpiVNwu5gWGpG9DepjR8B4YsKckQIVLNX09Q5oK5lc1w3iUny44eoZ4b/idgvm5WSaGuYT0U8s1GWIPALZoHyxQmzKvMuqb29S8v7xiJxRtmEa1qmoq3JtUKfMEpCQLDTmViAxpxk/krLzhkwuviAxB/aDgOvi4mEELLwX94tWtNeeTKqDRu/9uH22CImndw2tpcATWGAbwA8XLXM75vTIjRCwwZoxTwu04iItulCZ/RZQrbRGWkdEtUwUkvZZboWn7gJwIvshksKvMxlcT5QgkV8/yp82PmBoUI0AgS2NMN5HMQYSsLdgP4WUZTUUuRPbn0HMosyXEV2I3ZxAI60RIgbZQedCUk5okvOxeLlms+70ktlvwC+4M8hY8kDV8SsDRcSpwNszTtQ2cBN5ckxYhVijBeZ5YkDXb1BYgWGh5CDmKfJgglWLE5hPU4BeuP7MQWMb6eCERuKmo9bfzizyaYjBFZ18VAoMmD/kwuqb7e5V0YZo3MGF0LfmOMt0GIq67eYbbZ6iJVkSswKxeMyvFxWgqXBZqy6mM8qmF+oa9OeA+PESbLgFSh1C/jHaUDMVIlMOTN5i9wZecEVxDF0qxX4gUB3zBTDcYuJsgJ6gjQupN/8AZRvw9xAoutuXUoqtjdeoDYFDl3NmJc98M29lQPulRcZJQBWNy8I1j6CJTcPwCGrxUgRike6yQGhAUme31LwYFJ5Gd1FqLY7HNwVuOKq9PmCbpVNzWUAOjhA4hKxuA8QtNSpKlMltfmFUa8RKtBmguMmKGBn79ReaX3eIoB5XmDfIHUsqmaiSIQ1fEFNRUEW6l05i7ZDR2Hp4+JbgNX/EWIHvG5o+eNf+xGJloURLSU2kzg9xEKGlxCzHXyHmNMMEVp6eoq38pnRsiBUORFHGqzfTKJVgHrtFTzmGxjpOZB7JaZ7mFepZY0ZifKischUGtvCGy+miBrqWIRCkeSDXdXWF81ofMtLe7zAuLkThelF8JoHT4Df5lZiZiblCqdyvfqZBDC+5k4CZRanCHXxvG9XR5gFq2HIvthWBLL5v5HLtsdTqE6BEEXz9AtGCXy7Jeo5mPcrNFRPogBlppyXEJvQyOWAIZ6WUUFqN+oRcij5e/cLawuskvgtpDH3hS2R0koXoxjvzK6mxxBt1Z/mCDmTiWZIAINsWhbKMebzEBwTMpyMHmACR+jUunaIQFE7MTKx8TKxuZhIcKeBUMEMBAm0cGNbqBdlYjBppL0x6Neuh3CeBxcAQlfcMZEnSncH/AGlPQlL1FymBVr3NKcwKcQI3OIBtK/nqHnEJJlqpXZUANrWpUWy8Oyd6IhGWQLGPuG1rDFNnkTZ4lLQYoGvUM7fnlInqwI/qZXgx2XLs8Syl7S2Kq27hbdkMHkdrCFsnB3D0WowAgTR3Gm77ijhNDLLgKhaVkiatYOrxfxLPgaODzBMN0XePBOaHZKdxOczccTFOf3LIxbR8wPJBxmIbTfbG15hjd1MGFCKfhJYuc5P7RgZxgB9j6NtynHAtWxgBWtu7mKFepTmp4oKBLGHXbV1EtHU0uYqAcNjGY2QHhOIpI14mPk4jNyYOCphpZjAqRL5cfMdm0Ou4Lyd4+mjPMa/mHdAwbTAl0wBdwUXbz4lQDirzMfVpqWoewQyrcuU+t/mLjC75MoLz7iPjz+kvDUa2R1RNpNfeC23FbHuWa4eSVvzHsAZvczresRCQ6c8xsTpMY+cPlM94glSvcGoc2hg+YiGgJRIFwEfoGg0s4lCVonpcLLTN5/cu/E4ZT0FwLvqYIAOoBF6HUEdpI6I6CwbDk4Y2BwzfcUbc2wKiIAiWcwWVA1sQau4wGoTj/wBUcRWwdEr1SVQl1C3D4uBkIKNmQDBoV06gBNUMruWVuCWIavb4ldhFbOZVu4dgpmzT45IAasqvHh7io3kIdFlSQ1Yqq9kcF6IhYWzhEVZdMVPDl6mGc1E3z4xuYrOpgIKeisKpheVgiIu3YK+lgibILnJMTzShh9ooUwnMWWJehbi4tGr7RjaLtXUQ0gTnAYWNZV016iLXUa2SHJ/bPxL5G1atbYyWFuCUfQtPAwVIUUPOWWs1FCF0EyUXLiYtM/CYWNS7Kr3mojuyuSFBicR5+kwFi9niNwisjipVq+qYapbsV8IHjfL5IFi95gDcvwHqWKYMnT4hFoFqIFQ2rMXDEiENo8omTXdvL7SrXt1n2YTCp2U/iADWCb5ijxHcSyXS8KYi7laAOe5Rar0RzRbmYyqilmm0OIj+Y+sPFuPcGkXZXHccNOaSLkxStoEHUb6ICAXkAi43PNbCqRYtlw3RKTPcBYpyHjMuroFthptbwssvFqojTIdEDLdlxhlgslQmWdUNW8/hnGOerI+C7gzbMFC9sFyFZitUEHmLKZwHUNxhxmGi6NEbi8OW8yl+05Q8G0gr7ah6hq1SlZlox+hJLVmUXBSUOIFim53gdncVXJYVfEMWPIq/4jTAbsw+mXbHz5hphjhmS0ShC3XXmEWMOYObg9jXXEBWn2mA2SVAV+P2TEeafuHQ21a9sHgstuJZqKaZitrDe4ExDE5iwtRIBBxFNzIw1jqAy6PJLgis5bgWG8QNMQRzGqNyU1dxAZXM2ZXBcVg13yi2qI6zESrrq5aeUs1Dpwy9imuGO7u46p9AcfQKxcQTduSYC08i4gc9UB5hqlkh79kYKC6R4lYq0xDx8GeHqXbVkxUmwnH0uN6PlZwW2WNniWDW3U8NyjRBUaiiKwLONwNXLYNkWhviH+vPlh1DcoTuEkuApgi4tNcxNsS47l61cFGYZoivKYIjUg3nTDx6TqXMVzoXh78RAvSgoiNoU0wmKqc/q5kaO4LaNwKu+0zEUQORmjDaA0dhcaVBcGmuoFFAafPuLgo8PJKWUYH+ywNkfCf/AJy9cJgI7xetxi8SnzHMoUrMa8uPmCp9xgUc43EKXZ4l5ib99w/R5CKtXBSPg5emMI8bcP3I3yhysOn8OZZE2ZvxD7ENNpXywA9ae8VzK0TbrMpaVDqXazbEdjpwG7hlnmTuCsgsMGyDpzCgBglNyoZRzPP9Ny6cy1WUd3BrKETaYabqKarfOI0HqHMeo7+0Pp7fMJavgD1KFcl/Ec3G/qfRUQ5wETSJqvmZiMtO4xCHc7h1D+IjqvmsBzKdBvWVYhBFsHDct1EpLrq4Fsrp1GwgfhYurnyIoquwI1YJ6lpdncUJkTKy4M9GOLmxtfZlgYtInMPWC5Nkd2NTHMEwssixEI6Ku2AJXw3UUD4EHUfMV1shDADU3ufH8olPisakwx6gjvrZ0tdkr6Eo/wDMqHthkJQjVHmZjEQtWtS03MM4rMolWAwdzM4AgEBD7GIiWWZwhdxhIZq4OtdJpnnGtkXLGm55MuGbo4swR7YrzLrJfaFkTnqJiSW9X4g1G5aGLYSmK0VFNho6Fh6RZwkOln1BqajyzS1uVmoKXi+pVg6LGELh6gZuGcRhBi6V/EAiy0WWAlYzG09H2mD7jSGJbL1rWpr5uaBLqHGYyTZEvEPcUPgQ8lBVMABSjXmBlKtL5YN+BKX5lCWgrXMrKHInT4hQ3G+JWscTCzkGJM7iRFMS6TBESaVUKlVFbg7lDKRzUxCh6XcCpGm5ig3BkR/FVz5lVAxduYi+2aEEWBE6DuA+AsD3vqUgzV8DEmJ1zPLFGJlNBByrpuJVxiWL1BHkUetRcFTg2RFkg8VKEiExKBNiN9SYQSoLNWsBQVMsC3cFKFMat62cxMIQNxvGIj7xEX80hAyCp8Q3LGC5LNSpExnO/vLcrkvp9dwk9D0xBmJvOGO0Xr5i6T6LjEq1MSVNLgNqIbeJZD7RlZDNql13MGlRIn5Ze1YyplmHtztqMLy2+YLQTdVxCjwCtSmFTRRVefMJCLV0l0VQR+CBdnnB93/IyA/Cg8cvzEEn9mKS8ruIo7ZcGrh1wG+IwxUe5jhjIm2I2d8k85wZSNpD3EdlPcFhLKZPtLvDiIxM2W0rRdC5DxEttSgUk8PEHJfMTsH5EQLVyq0P+RdGRRwQZYVfedfiKOQID1NCqA0Ey1WYO2aifbGNI5WHuGrxsCHoK4sVmVkAPMfauL5ityumEBVcOWsZpDCBi1wVVifaWwfEZWUbRNBtl+bwsG2IAxzFHjdCeEdPYbgU0ZQOu5YM6N+JR0sBWxDF+Kv5mTAAgqQXI3BBdGSJ4FtQPfiSjfMRNS1zDXb6YEw4Ktpi11j6JG3zLniocvmDF5d3kfzFaO+5cwdLhwcBiEG7Cd4mQ+pvn5sFjYZvmZGyKf8AkvExS+CA8IFneYQxQKYyUFHbGppQJ4ywAqxZ/YUgV2nuGi2Nn3iUilC4gZyXMZEuZz4ksjasAYqAGnqaQXtcwnThq+IGAUuT5hcg5agMil2ysXixUagNBcw1KTiZB2avMQyYl5Bw4nVbdUQgmi+Ju+gk2dTH5TiJicwmHmAWxO/p/9kA" alt="" />



使用OpenCV&&C++进行模板匹配.的更多相关文章
- 使用Opencv中matchTemplate模板匹配方法跟踪移动目标
模板匹配是一种在图像中定位目标的方法,通过把输入图像在实际图像上逐像素点滑动,计算特征相似性,以此来判断当前滑块图像所在位置是目标图像的概率. 在Opencv中,模板匹配定义了6种相似性对比方式: C ...
- 使用Python+OpenCV进行图像模板匹配(Match Template)
2017年9月22日 BY 蓝鲸 LEAVE A COMMENT 本篇文章介绍使用Python和OpenCV对图像进行模板匹配和识别.模板匹配是在图像中寻找和识别模板的一种简单的方法.以下是具体的步骤 ...
- OpenCV中的模板匹配/Filter2d
1.模板匹配 模板匹配是在图像中寻找目标的方法之一.Come On, Boy.我们一起来看看模板匹配到底是怎么回事. 参考链接:http://www.opencv.org.cn/opencvdoc/2 ...
- opencv如何用模板匹配寻找目标
首先使用: MatchTemplate 比较模板和重叠的图像区域 void cvMatchTemplate( const CvArr* image, const CvArr* templ, CvArr ...
- opencv 单目标模板匹配(只适用于模板与目标尺度相同)
#include <iostream> #include "opencv/cv.h" #include "opencv/cxcore.h" #inc ...
- Opencv for android 模板匹配
因为有这方面的需要所以,对模板查找搜寻了相关资料,只是对于算法的东西很难看得动,特别是opencv涉及的很多的数学方法. 所以只为了实现这个功能,因为需求比较简单,在网上也搜寻到了相关代码,就直接拿来 ...
- OpenCV-Python 模板匹配 | 三十一
目标 在本章中,您将学习 使用模板匹配在图像中查找对象 你将看到以下功能:cv.matchTemplate(),cv.minMaxLoc() 理论 模板匹配是一种用于在较大图像中搜索和查找模板图像位置 ...
- opencv 模板匹配与滑动窗口(单匹配) (多匹配)
1单匹配: 测试图片: code: #include <opencv\cv.h> #include <opencv\highgui.h> #include <open ...
- opencv 在工业中的应用:模板匹配
模板匹配在工业中经常有两个用途,一模板匹配进行产品定位,二根据匹配度来判断是OK的产品还是NG的产品.我用OPENCV做了个模板匹配定位的DEMO. (1)点击打开图像按钮打开一幅图像 (2)点击定义 ...
随机推荐
- 声明变量,一定要用 var!
public static T TryGet<T>(Func<T> func, T ifError = default(T)) { try { return func(); } ...
- php知识案列分享
今天再跟大家分享一下,以下案列. 使用array_flip函数生成随机数,可以去掉重复值. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 < ...
- P3P设置第三方cookie解决方案
原文地址:http://blog.csdn.net/lovingprince/article/details/5984449 首先,什么是 P3P ( Platform for Privacy Pre ...
- 《Linux内核设计与实现》课本第五章学习笔记——20135203齐岳
<Linux内核设计与实现>课本第五章学习笔记 By20135203齐岳 与内核通信 用户空间进程和硬件设备之间通过系统调用来交互,其主要作用有三个. 为用户空间提供了硬件的抽象接口. 保 ...
- SAX和DOM解析的区别
XML和JSon是ios解析文件的两种形式, 两种方法各有千秋. 1>. XML分为SAX和DOM两种方式 SAX是按顺序逐行读取文件, 查找到符合条件的内容时就会停止, 而DOM是讲内容一次性 ...
- vue新建项目
一直都被如何用vue.js新建一个项目的问题困扰着,经过好久的实践,终于搞清楚如何用vue新建项目了: 1.官网对于vue-cli介绍: Vue.js provides an official CLI ...
- ORBSLAM2与OPENCV3.1.0出错解决办法
用opencv3.1.0做ORBSLAM2运行一下命令时cd ORB_SLAM2 chmod +x build.sh ./build.sh出错:/usr/bin/ld: CMakeFiles/mono ...
- hello 漂亮的小靓仔
<form type="text" name="超级" method="post"> <table align=" ...
- checkbox
$(document).ready(function(){ var page_id = {/$page_id/}; var location_id = {/$location_id/}; var lo ...
- IIS 7.5 发布Web 网站步骤
1. 添加删除程序中,点击打开或关闭Window 功能 , 如图 , 勾选: 2. 打开 vs开发工具 控置台程序 , 注册 aspnet_regiis -i 3.设置应用程序域为指定版本 4.设置应 ...
