C# 实现 任意多边形切割折线算法

1.    内容简介

本文旨在解决任意多边形切割折线，获取切割之后的折线集合。

本文实现的算法内容包括：判断两条线段是否相交,如若相交，获取交点集合、对线上的点集，按斜率方向排序、判断点是否在多边形内、获取线段和任意多边形的交点集合、中点算法、获取任意多边形裁剪折线的线段集合。

2.    效果实现

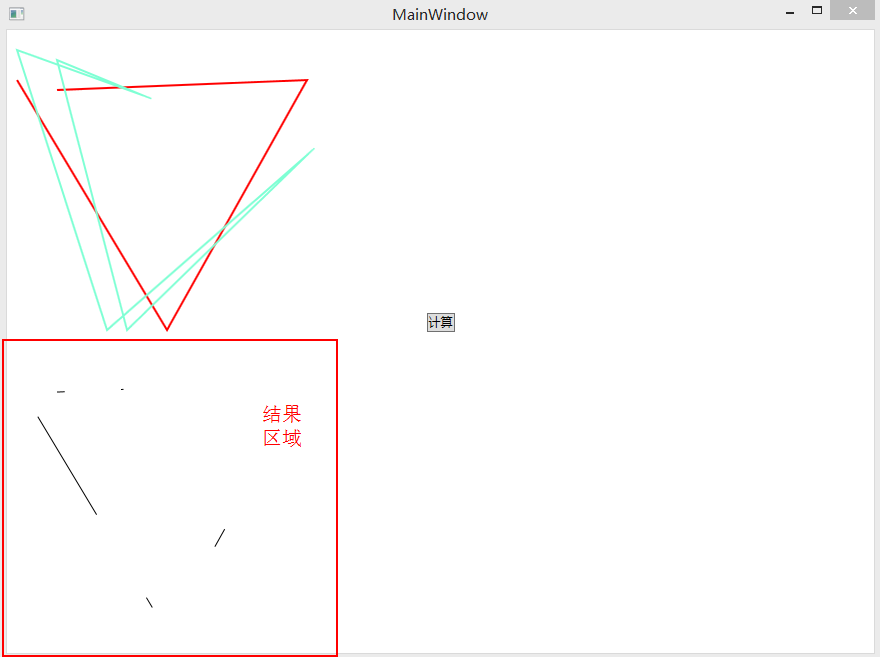
3.    算法实现

a)    本文使用到的命名空间

using System;
using System.Collections.Generic;
using System.Linq;
using System.Windows;
using System.Windows.Shapes;

命名空间

b)    源代码实现

 public partial class Help
    {

        #region 线段与多边形的交点集合，按从p1到p2的方向进行排序
        /// <summary>
        /// 对一线段与多边形的交点集合，按从p1到p2的方向进行排序
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <param name="interPoints"></param>
        /// <returns></returns>
        public List<Point> SortPointsBySlopeOfLine(Point p1, Point p2, List<Point> interPoints)
        {
            List<Point> points = new List<Point>();
            List<Point> newInterPoints = new List<Point>();
            points.Add(p1);
            if (Equals(p1.X, p2.X))//垂直线段
            {
                if (p1.Y > p2.Y)
                {
                    newInterPoints = interPoints.OrderByDescending(t => t.Y).ToList();
                }
                else
                {
                    newInterPoints = interPoints.OrderBy(t => t.Y).ToList();
                }
            }
            else
            {
                if (Equals(p1.Y, p2.Y))//水平线段
                {
                    if (p1.X > p2.X)
                    {
                        newInterPoints = interPoints.OrderByDescending(t => t.X).ToList();
                    }
                    else
                    {
                        newInterPoints = interPoints.OrderBy(t => t.X).ToList();
                    }

                }
                else//普通斜率线段，按x或y都行
                {
                    if (p1.X > p2.X)
                    {
                        newInterPoints = interPoints.OrderByDescending(t => t.X).ToList();
                    }
                    else
                    {
                        newInterPoints = interPoints.OrderBy(t => t.X).ToList();
                    }

                }

            }

            foreach (Point interPoint in newInterPoints)
            {
                points.Add(interPoint);
            }
            points.Add(p2);
            return points;
        }
        #endregion

        #region 获取线段和线段的交点

        private double eps = 1e-;
        /// <summary>
        /// 判断一个数值是否在误差范围内
        /// </summary>
        /// <param name="x"></param>
        /// <returns></returns>
        private bool zero(double x)
        {

            return (((x) >  ? (x) : -(x)) < eps);
        }

        /// <summary>
        /// 计算交叉乘积(P1-P0)x(P2-P0)
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <param name="p0"></param>
        /// <returns></returns>
        private double xmult(Point p1, Point p2, Point p0)
        {
            return (p1.X - p0.X) * (p2.Y - p0.Y) - (p2.X - p0.X) * (p1.Y - p0.Y);
        }

        /// <summary>
        /// 判点是否在线段上,包括端点
        /// </summary>
        /// <param name="p"></param>
        /// <param name="l1"></param>
        /// <param name="l2"></param>
        /// <returns></returns>
        private bool dot_online_in(Point p, Point l1, Point l2)
        {
            return zero(xmult(p, l1, l2)) && (l1.X - p.X) * (l2.X - p.X) < eps && (l1.Y - p.Y) * (l2.Y - p.Y) < eps;
        }

        /// <summary>
        /// 判两点在线段同侧,点在线段上返回0
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <param name="l1"></param>
        /// <param name="l2"></param>
        /// <returns></returns>
        private bool same_side(Point p1, Point p2, Point l1, Point l2)
        {
            return xmult(l1, p1, l2) * xmult(l1, p2, l2) > eps;
        }

        /// <summary>
        /// 判断两直线平行
        /// </summary>
        /// <param name="u1"></param>
        /// <param name="u2"></param>
        /// <param name="v1"></param>
        /// <param name="v2"></param>
        /// <returns></returns>
        private bool parallel(Point u1, Point u2, Point v1, Point v2)
        {
            return zero((u1.X - u2.X) * (v1.Y - v2.Y) - (v1.X - v2.X) * (u1.Y - u2.Y));
        }

        /// <summary>
        /// 判三点共线
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <param name="p3"></param>
        /// <returns></returns>
        private bool dots_inline(Point p1, Point p2, Point p3)
        {
            return zero(xmult(p1, p2, p3));
        }

        /// <summary>
        /// 判两线段相交,包括端点和部分重合
        /// </summary>
        /// <param name="u1"></param>
        /// <param name="u2"></param>
        /// <param name="v1"></param>
        /// <param name="v2"></param>
        /// <returns></returns>
        private bool intersect_in(Point u1, Point u2, Point v1, Point v2)
        {
            if (!dots_inline(u1, u2, v1) || !dots_inline(u1, u2, v2))
                return !same_side(u1, u2, v1, v2) && !same_side(v1, v2, u1, u2);
            return dot_online_in(u1, v1, v2) || dot_online_in(u2, v1, v2) || dot_online_in(v1, u1, u2) || dot_online_in(v2, u1, u2);
        }

        /// <summary>
        /// 计算两线段交点,请判线段是否相交(同时还是要判断是否平行!)
        /// </summary>
        /// <param name="u1"></param>
        /// <param name="u2"></param>
        /// <param name="v1"></param>
        /// <param name="v2"></param>
        /// <param name="ret"></param>
        /// <returns></returns>
        private int GetIntersectionPoint(Point u1, Point u2, Point v1, Point v2, out Point ret)
        {
            ret = u1;
            if (parallel(u1, u2, v1, v2) || !intersect_in(u1, u2, v1, v2))
            {
                return ;
            }
            double t = ((u1.X - v1.X) * (v1.Y - v2.Y) - (u1.Y - v1.Y) * (v1.X - v2.X))
              / ((u1.X - u2.X) * (v1.Y - v2.Y) - (u1.Y - u2.Y) * (v1.X - v2.X));
            ret.X += (u2.X - u1.X) * t;
            ret.Y += (u2.Y - u1.Y) * t;
            return ;
        }
        #endregion

        #region 多边形包含点
        /// <summary>
        /// 判断多边形是否包含某个点
        /// </summary>
        /// <param name="poly">多边形边框上每个角的点坐标数组</param>
        /// <param name="p">要进行判断的点</param>
        /// <returns>true:包含; false:不包含</returns>
        public bool InPoly(Polygon polygon, Point p)
        {

            Point[] poly = polygon.Points.ToArray();
            int i = , f = ;
            double xi = , a = , b = , c = ;
            Point ps, pe;
            ///遍历每一个点
            /// Microsoft.VisualBasic.Information.UBound 获取最大下标，等同于 poly.Count-2
            for (i = ; i <= Microsoft.VisualBasic.Information.UBound(poly, ); i++)
            {
                ps = poly[i];

                if (i < Microsoft.VisualBasic.Information.UBound(poly, ))
                {
                    pe = poly[i + ];
                }
                else
                {
                    pe = poly[];
                }
                GetStdLine(ps, pe, ref a, ref b, ref c);
                if (a != )
                {
                    xi =  - ((b * p.Y + c) / a);
                    if (xi == p.X)
                    {
                        return true;
                    }
                    else if (xi < p.X)
                    {
                        f = f + Sgn(pe.Y - p.Y) - Sgn(ps.Y - p.Y);
                    }
                }
            }
            return f != ;
        }

        /// <summary>
        /// 根据两个点的坐标求经过两点的直线的标准方程参数A、B、C
        /// </summary>
        /// <param name="ps"></param>
        /// <param name="pe"></param>
        /// <param name="a"></param>
        /// <param name="b"></param>
        /// <param name="c"></param>
        private void GetStdLine(Point ps, Point pe, ref double a, ref double b, ref double c)
        {
            double xs, ys, xe, ye;
            double p1, p2;
            xs = ps.X;
            ys = ps.Y;
            xe = pe.X;
            ye = pe.Y;
            p1 = (xs * ye);
            p2 = (xe * ys);
            if (p1 == p2)
            {
                if (xs == )
                {
                    if (xe == )
                    {
                        a = ;
                        b = ;
                        c = ;
                    }
                    else if (ys == )
                    {
                        a = ye;
                        b =  - xe;
                        c = ;
                    }
                }
                else if (ye == )
                {
                    if (ys == )
                    {
                        a = ;
                        b = ;
                        c = ;
                    }
                    else if (xe == )
                    {
                        a =  - ys;
                        b = xs;
                        c = ;
                    }
                }
            }
            else
            {
                a = (ys - ye) / (p1 - p2);
                c = ;
                if (ys == )
                {
                    if (ye == )
                    {
                        b = ;
                        c = ;
                    }
                    else
                    {
                        b =  - ((a * xe + ) / ye);
                    }
                }
                else
                {
                    b =  - ((a * xs + ) / ys);
                }
            }
        }
        private int Sgn(double a)
        {
            if (a == )
            {
                return ;
            }
            else if (a < )
            {
                return -;
            }
            else
            {
                return ;
            }
        }

        #endregion

        /// <summary>
        /// 求出线段和多边形的交点,不包括p1p2
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <param name="polygon"></param>
        /// <returns></returns>
        public List<Point> GetInterPoints(Point p1, Point p2, Polygon polygon)
        {
            List<Point> interPoints = new List<Point>();
            List<Point> polygonPoints = polygon.Points.ToList();
            for (int i = ; i < polygonPoints.Count; i++)
            {
                Point polygon1 = polygonPoints[i];
                Point polygon2 = new Point();
                if (i == polygonPoints.Count - )
                {
                    polygon2 = polygonPoints[];
                }
                else
                {
                    polygon2 = polygonPoints[i + ];

                }
                Point inter = new Point();
                int interType = GetIntersectionPoint(p1, p2, polygon1, polygon2, out inter);
                switch (interType)
                {

                    case :

                        if (!Equals(inter, p1) && !Equals(inter, p2))
                        {
                            interPoints.Add(inter);
                        }
                        break;
                    case :
                    default:
                        break;
                }
            }
            return interPoints;
        }

        /// <summary>
        /// 取两个点的中点
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <returns></returns>
        public Point GetCenter(Point p1, Point p2)
        {
            return new Point((p1.X + p2.X) / , (p1.Y + p2.Y) / );
        }

        /// <summary>
        /// 获取多边形裁剪折线形成的线段集合
        /// </summary>
        /// <param name="polyline"></param>
        /// <param name="polygon"></param>
        /// <returns></returns>
        public List<Polyline> GetInterPolylines(Polyline polyline, Polygon polygon)
        {
            List<Polyline> list = new List<Polyline>();
            //TODO： 1.遍历折线上的每相邻的两个个点，组成线段，与多边形的每一条边计算，求出此线段与多边形的边的交点
            //TODO:  2.对此线段的上的交点进行排序，组成连续点的折线，判断这些线段在多边形内部的部分，加入集合

            List<Point> polinePoints = polyline.Points.ToList();
            List<Point> polygonPoints = polygon.Points.ToList();

            for (int i = ; i < polinePoints.Count - ; i++)
            {
                Point one = polinePoints[i];
                Point two = new Point();
                if (i == polinePoints.Count - )
                {

                }
                else
                {
                    two = polinePoints[i + ];
                }
                List<Point> inters = GetInterPoints(one, two, polygon);
                List<Point> sortInters = SortPointsBySlopeOfLine(one, two, inters);

                for (int j = ; j < sortInters.Count; j++)
                {
                    if (j < sortInters.Count - )
                    {
                        if (InPoly(polygon, GetCenter(sortInters[j], sortInters[j + ])))
                        {
                            Polyline interPolyline = new Polyline();
                            interPolyline.Points.Add(sortInters[j]);
                            interPolyline.Points.Add(sortInters[j + ]);
                            list.Add(interPolyline);
                        }
                    }

                }
            }
            return list;
        }
    }

SourceCode