[NOIP2015] 提高组 洛谷P2668 斗地主

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。

具体规则如下：

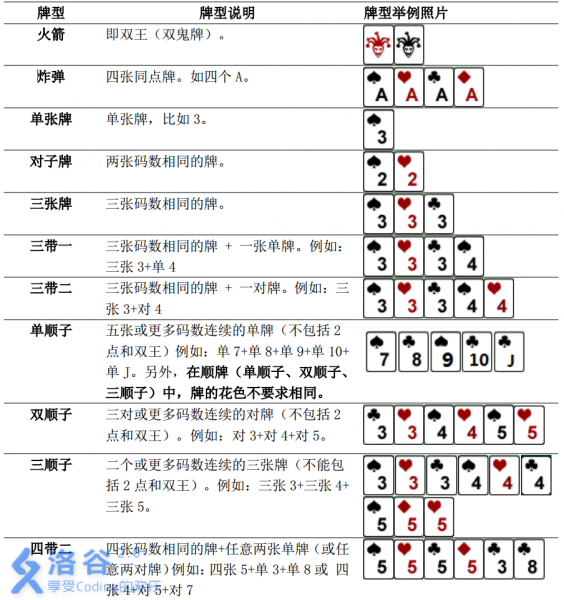
输入输出格式

输入格式：

第一行包含用空格隔开的2个正整数T和n，表示手牌的组数以及每组手牌的张数。

接下来T组数据，每组数据n行，每行一个非负整数对aibi表示一张牌，其中ai示牌的数码，bi表示牌的花色，中间用空格隔开。特别的，我们用1来表示数码A，11表示数码J，12表示数码Q，13表示数码K；黑桃、红心、梅花、方片分别用1-4来表示；小王的表示方法为01，大王的表示方法为02。

输出格式：

共T行，每行一个整数，表示打光第i手牌的最少次数。

输入输出样例

输入样例#1：

1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1

输出样例#1：

3

输入样例#2：

1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2

输出样例#2：

6

说明

样例1说明

共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。

对于不同的测试点， 我们约定手牌组数T与张数n的规模如下：

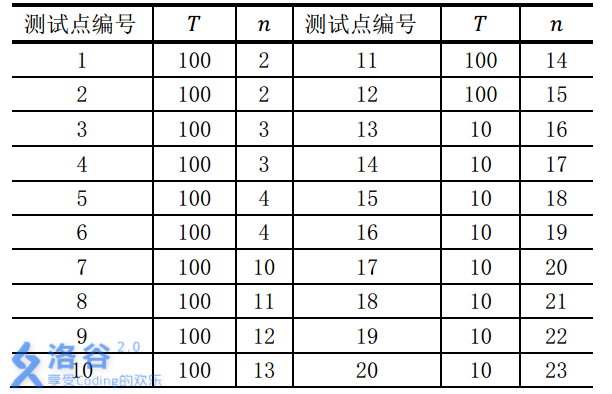
数据保证：所有的手牌都是随机生成的。

搜索

 /*by SilverN*/
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 const int mxn=;
 int cnt[mxn],r[mxn];
 int ans;
 int T,n;
 int query(){
     int tot=;
     memset(r,,sizeof r);
     for(int i=;i<=;i++)
         r[cnt[i]]++;
     while(r[] && r[]>=)r[]--,r[]-=,tot++;
     while(r[] && r[]>=)r[]--,r[]-=,tot++;
     while(r[] && r[])r[]--,r[]--,tot++;
     while(r[] && r[])r[]--,r[]--,tot++;
     while(r[] && r[])r[]--,r[]--,tot++;
     return tot+r[]+r[]+r[]+r[];
 }
 void dfs(int time){
     if(time>=ans) return;
     int tmp=query();
     if(time+tmp<ans)ans=tmp+time;
     int i,j,x;
     for(i=;i;i--)
         for(j=;j<=;j++){
             x=j;
             while(cnt[x]>=i){
                 x++;
                 if((i== && x-j>=)||(i== && x-j>=)||(i== && x-j>=)){
                     for(int k=j;k<x;k++) cnt[k]-=i;
                     dfs(time+);
                     for(int k=j;k<x;k++) cnt[k]+=i;
                 }
             }
         }
 }
 int main(){
     scanf("%d%d",&T,&n);
     int i,j;
     while(T--){
         memset(cnt,,sizeof cnt);
         ans=n;
         for(i=;i<=n;i++){
             int a;
             scanf("%d%*d",&a);
             if(a==)a=;
             else if(a)a--;
             cnt[a]++;
         }
         dfs();
         printf("%d\n",ans);
     }
     return ;
 }