【转】C语言快速幂取模算法小结

(转自:http://www.jb51.net/article/54947.htm)

本文实例汇总了C语言实现的快速幂取模算法，是比较常见的算法。分享给大家供大家参考之用。具体如下：

首先，所谓的快速幂，实际上是快速幂取模的缩写，简单的说，就是快速的求一个幂式的模(余)。在程序设计过程中，经常要去求一些大数对于某个数的余数，为了得到更快、计算范围更大的算法，产生了快速幂取模算法。我们先从简单的例子入手：求abmodc

算法1.直接设计这个算法：

int ans = ;
for(int i = ;i<=b;i++)
{
  ans = ans * a;
}
ans = ans % c;

缺点：这个算法存在着明显的问题，如果a和b过大，很容易就会溢出。

我们先来看看第一个改进方案：在讲这个方案之前，要先看这样一个公式：ab mod c = (a mod c)c mod c

于是不用思考的进行了改进：

算法2.改进算法：

int ans = ;
a = a % c; //加上这一句
for(int i = ;i<=b;i++)
{
  ans = ans * a;
}
ans = ans % c;

读者应该可以想到，既然某个因子取余之后相乘再取余保持余数不变，那么新算得的ans也可以进行取余，所以得到比较良好的改进版本。

算法3.进一步改进算法：

int ans = ;
a = a % c; //加上这一句
for(int i = ;i<=b;i++)
{
  ans = (ans * a) % c;//这里再取了一次余
}
ans = ans % c;

这个算法在时间复杂度上没有改进，仍为O(b)，不过已经好很多的，但是在c过大的条件下，还是很有可能超时，所以，我们推出以下的快速幂算法。

算法4.快速幂算法：

快速幂算法依赖于以下明显的公式：

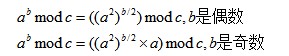
int PowerMod(int a, int b, int c)
{
  int ans = ;
  a = a % c;
  while(b>) {
    if(b %  = = )
    ans = (ans * a) % c;
    b = b/;
    a = (a * a) % c;
  }
  return ans;
}

本算法的时间复杂度为O（logb），能在几乎所有的程序设计（竞赛）过程中通过，是目前最常用的算法之一。

相信本文所述对大家算法设计的学习有一定的借鉴价值。