c++ 逆序对
c++ 求逆序对
例如数组(3,1,4,5,2)的逆序对有(3,1)(3,2)(4,2)(5,2)共4个
逆序对就是左边的元素比右边的大,那么左边的元素和右边的元素就能产生逆序对
代码跟归并排序差不多
代码
#include <bits/stdc++.h>
using namespace std;
int a[100];
int r[100];
int ans = 0;
void sort(int s,int t)
{
if (s == t)
return ;
else
{
int mid = (s + t) / 2;
sort(s,mid);//排序mid前面部分
sort(mid + 1,t);//排序好mid后面部分
int i = s,j = mid + 1,k = s;
while (i <= mid && j <= t)
{
if (a[i] <= a[j])
{
r[k] = a[i];
k ++;
i ++;
}
else
{
r[k] = a[j];
k ++;
j ++;
//ans += mid - i + 1;
ans = ans + mid - i + 1;//逆序对个数公式
}
}
while (i <= mid)
{
r[k] = a[i];
k ++;
i ++;
}
while (j <= t)
{
r[k] = a[j];
k ++;
j ++;
}
for (int i = s;i <= t;i ++)
a[i] = r[i];
}
}
int main()
{
int n;
cin >> n;
for (int i = 1;i <= n;i ++)//输入
{
cin >> a[i];
}
sort(1,n);
cout << ans << endl;//ans就是逆序对的个数
cout << endl;
return 0;
}
理解
对于ans = ans + mid - i + 1这个公式,我是这么理解的
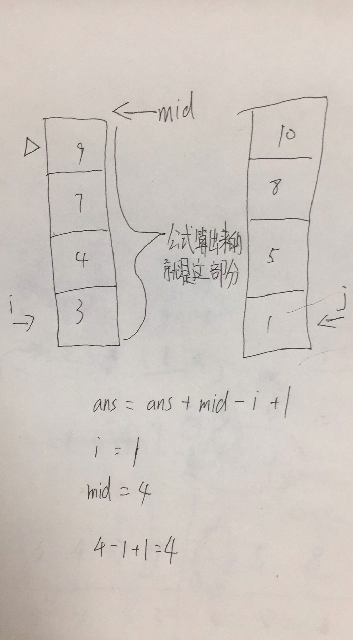
c++ 逆序对的更多相关文章
- 【CQOI2011】动态逆序对 BZOJ3295
Description 对于序列A,它的逆序对数定义为满足i<j,且Ai>Aj的数对(i,j)的个数.给1到n的一个排列,按照某种顺序依次删除m个元素,你的任务是在每次删除一个元素之前统计 ...
- CH Round #72 奇数码问题[逆序对 观察]
描述 你一定玩过八数码游戏,它实际上是在一个3*3的网格中进行的,1个空格和1~8这8个数字恰好不重不漏地分布在这3*3的网格中. 例如:5 2 81 3 _4 6 7 在游戏过程中,可以把空格与其上 ...
- POJ3928Ping pong[树状数组 仿逆序对]
Ping pong Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 3109 Accepted: 1148 Descrip ...
- NOIP2013火柴排队[逆序对]
题目描述 涵涵有两盒火柴,每盒装有 n 根火柴,每根火柴都有一个高度. 现在将每盒中的火柴各自排成一列, 同一列火柴的高度互不相同, 两列火柴之间的距离定义为: ∑(ai-bi)^2 其中 ai 表示 ...
- bzoj 3295 动态逆序对 CDQ分支
容易看出ans[i]=ans[i-1]-q[i],q[i]为删去第i个数减少的逆序对. 先用树状数组算出最开始的逆序对,预处理出每个数前边比它大的和后边比它小的,就求出了q[i]的初始值. 设b[i] ...
- 诸城模拟赛 dvd的逆序对
[题目描述] dvd是一个爱序列的孩子. 他对序列的热爱以至于他每天都在和序列度过 但是有一个问题他却一直没能解决 给你n,k求1~n有多少排列有恰好k个逆序对 [输入格式] 一行两个整数n,k [输 ...
- 归并求逆序数(逆序对数) && 线段树求逆序数
Brainman Time Limit: 1000 MS Memory Limit: 30000 KB 64-bit integer IO format: %I64d , %I64u Java c ...
- BZOJ 3295: [Cqoi2011]动态逆序对
3295: [Cqoi2011]动态逆序对 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 3865 Solved: 1298[Submit][Sta ...
- BZOJ 3295 【Cqoi2011】 动态逆序对
Description 对于序列\(A\),它的逆序对数定义为满足\(i<j\),且\(A_i>A_j\)的数对\((i,j)\)的个数.给\(1\)到\(n\)的一个排列,按照某种顺序依 ...
- 【bzoj3295】 Cqoi2011—动态逆序对
http://www.lydsy.com/JudgeOnline/problem.php?id=3295 (题目链接) 题意 给出某种排列,按照某种顺序依次删除m个数,在每次删除一个数前统计序列中逆序 ...
随机推荐
- WPF DataGrid自定义列DataGridTextColumn.ElementStyle和DataGridTemplateColumn.CellTemplate
<Window x:Class="DataGridExam.MainWindow" xmlns="http://schemas.microsoft.c ...
- JS如何为iframe添加onclick事件
如果页面上有iframe时,鼠标点击在iframe内时,包含iframe的document是不响应任何事件的, 例如: $("#iframe1").click(function() ...
- 深入理解Amazon Alexa Skill(三)
本节来讨论Alexa Skill中涉及到的授权问题. Alexa内功能的授权 Alexa会发给skill用户的token,然后skill代码使用这个token来访问Web API访问用户的Alexa内 ...
- SQL Server 限制IP登陆(登陆触发器运用)
原文:SQL Server 限制IP登陆(登陆触发器运用) 一.本文所涉及的内容(Contents) 本文所涉及的内容(Contents) 背景(Contexts) 实现代码(SQL Codes) 补 ...
- git pull和fetch的区别
详解git pull和git fetch的区别: - weixin_41975655的博客 - CSDN博客 https://blog.csdn.net/weixin_41975655/article ...
- C#从列表中取元素的某个字段组成新的列表
using System; using System.Collections.Generic; using System.Linq; namespace CSharpDemo { class Prog ...
- Delphi皮肤之 - 图片按钮
效果如图,支持普通.移上去.按下.弹起.禁用5种状态. unit BmpBtn; interface uses Windows, Messages, SysUtils, Classes, Graphi ...
- delphi中move函数的正确理解(const和var一样,都是传地址,所以Move是传地址,而恰恰不是传值)太精彩了 good
我们能看到以下代码var pSource,pDest:PChar; len: integer;.......................//一些代码Move(pSource,pDest,l ...
- Markdown 语法简体中文版
Markdown 语法简体中文版(fork 于繁体中文版 http://markdown.tw/ ) http://wowubuntu.com/markdownhttps://github.com/r ...
- 剖析Unreal Engine超真实人类的渲染技术Part 1 - 概述和皮肤渲染
一.概述 1.1 数字人类的概要 数字人类(Digital Human)是利用计算机模拟真实人类的一种综合性的渲染技术.也被称为虚拟人类.超真实人类.照片级人类. 它是一种技术和艺术相结合的综合性模拟 ...
