day3（数论）

总得来说，这是可怕的一天，极其可怕的一天（完）

一、数论

阴影啊！

首先，设ab为两个整数，则存在唯一的q和r，使得a=qb+r

若r=0，则b整除a，记作b|a。

（1）同余

若a/m和b/m的余数相同,则称a于b对模m同余,记作a ≡ b (mod m)

剩余系:在模 m 的意义下，余数相同的数归为一个集合，那么所有整数被分为 m个不同的集合，模 m 的余数分别为 0,1,2,3,...,m − 1，这些集合被称为模 m 剩余类（同余类）。每个同余类中的任意两个整数都是模 m 同余的。__by dzy（就是模m的余数集合）

若是剩余系遍历了0~m-1，则叫做完全剩余系

• 同余式的三则运算：

• 设 a,b,c,d 为整数，m 为正整数，若 a ≡ b (mod m),c ≡ d(mod m)，则：

• ax + cy ≡ bx + dy (mod m)，其中 x,y 为任意整数，即同余式可以相加（）
• ac ≡ bd (mod m)，即同余式可以相乘a n ≡ b n (mod m)，其中 n > 0
• f(a) ≡ f(b) (mod m)，其中 f(x) 为任一多项式。
• a n ≡ b n (mod m)，其中 n > 0

（2）素数

判断素数的方法：一般是从2开始，枚举到√ n，依次判断i是否能整除n，若n=pq，则pq中的一个必定小于等于√ n。

但是，如果硬生生跑√ n，那么如果需要素数的话可能会把评测姬卡哭喔

所以我们需要：

素数筛

原理1：考虑在每找到一个素数的时候把它的倍数也标记上。这样就可以实现：大大减少

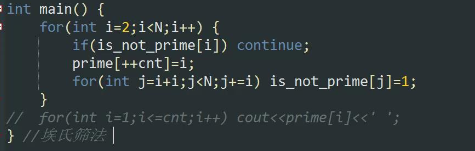
复杂度：O(nloglogn）基本达到线性。

但是它还有优化的空间：

比如12，跑到2的时候它被筛了一次，跑到3的时候它又被干了一次

所以极端情况评测姬还是会被卡哭....

我们强制命令每一个数都只被它的最小质因数给筛去，

于是，伟大的线性筛出生了

原理2：每一个数都只被它的最小质因数给筛去

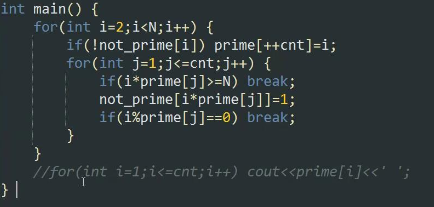
下for解释：

如果大于上界，退出，

标记非质数

如果i被之前的素数筛过了（这里保证了线性，即每个数只来一遍）

三、欧拉函数（φ（n））是指不超过n且与n互质的数的个

• p是一个质数，则φ（p）=p-1（除了1都与p互质）（逆定理依旧成立）
• p是质数，a是正整数，则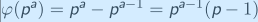（显然只有p的倍数与p^a 不互质，故可得到上式）

• 如果mn互质，则φ（mn）=φ（m）*φ（n）必须互质！！（证明长啊。。。甩个链接https://cdn.luogu.org/upload/pic/69862.png）

欧拉定理：如果a，m互质，那么：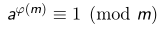

此证明不难理解：

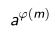*x1 * x2 * x3.....xφ（m）≡x1 * x2 * x3.....xφ（mod m）

同除

x1x2x3......

得

常用的是：费马小定理

当 p 是质数,a ̸= p 时，有 a p−1 ≡ 1 (mod p)。。

广义欧拉定理：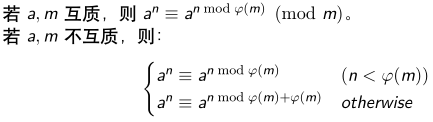

证明是真的不会....放链接https://blog.csdn.net/zxyoi_dreamer/article/details/82929466

四、gcd部分

lcm（最小公倍数）（a，b）=ab/gcd（a，b）；

求算gcd：欧几里得算法（辗转相除）

原理：gcd（a，b）=gcd（b，a-b）

设 (a,b) = g,a = cg,b = dg，那么 (c,d) = 1。
(b,a − b) = (d,c − d)g。
如果 (d,c − d) = q ̸= 1，那么 (c,d) ≥ q ̸= 1，矛盾。
所以 (b,a − b) = (d,c − d)g = g。

所以gcd就诞生了

int gcd(int a,int b)
{
    if(b==)return a;
    else gcd(b,a%b);
}（短小精悍）

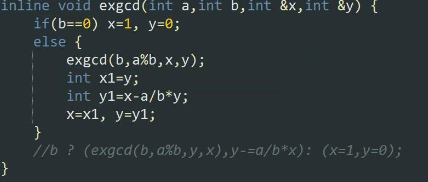
exgcd（一次不定方程）

考虑求解方程：ax+by=c

有解的情况是：gcd（a，b）|c。

当b=0，gcd（a，b）=a；

当b！=0，gcd（a，b）=gcd（b，a%b）；

所以原方程——>bx2+（a%b）y2=gcd（b，a%b）

于是我们就可以递归求解。

五、逆元

在一些情况下，（比如组合数）要边除边膜，这样可能暴毙。。。

所以逆元登场了。除一个数等于乘一个数的倒数，所以逆元就是除数膜的倒数

来看看正经的定义：

若（a，m）=1，且ab≡ 1 (mod m)，则b就是a%m意义下的逆元。

（a/b≡ a ∗ c (mod m)）

求解逆元的方法：

1、费马小定理

根据定义，ab≡ 1 (mod m)，及费马小定理，得：

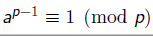
所以a^(p-2)*a≡1（mod p）所以得a^p-2是a的逆元

2、exgcd

已知exgcd可用于求解ax+by=1的解，那么exgcd怎么求算逆元呢？

如果ax+by=1，则ax≡1（mod m）所以x就是a在模m意义下的逆元。

3、线性递推

https://www.cnblogs.com/qdscwyy/p/7795368.html

六、多元一次不定方程

1、二元一次不定方程

exgcd.....系数同除以c，然后解再乘上c就行了

2、多元方程组

n元一次不定方程：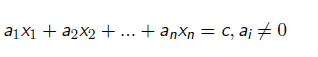

当且仅当(a1; a2; :::; an)|c，方程有解。

怎么解呢？

设(a1; a2) = d2; (d2; a3) = d3; :::; (dn-1; an) = dn，那么方程等价于：

于是可以从最后一个开始求，然后代回去，直到第一个。

3、一元线性同于方程：

形如ax≡b (mod m)

等价于ax-my=b，直接exgcd即可。

形如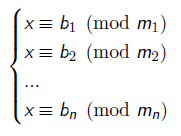

的可爱方程组~（彻底败给了dzy大神的讲解顺序啊....先exCRT再CRT.....真的醉了）

（1）CRT解法 限制：m1，m2，互质，若m不互质，甚至可以质因数分解强行互质.....

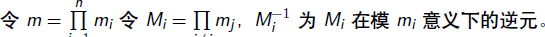
令ei=1/Mi*Mi mod m

则：

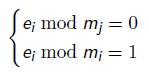
所以，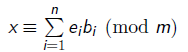

（2）exCRT（合并法）

考虑两两合并：

由于x≡b（mod m）等价于x-my=b，

当：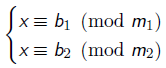

根据上述展开，得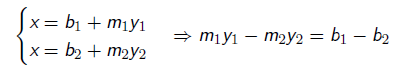

所以，我们令m=lcm（m1，m2），此方程就变成了：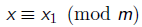

最后得到一个方程，那么这个解就是最终解

七、神仙

实在是看不懂，老师也没有讲，果然还是我太弱了