子字符串查找之————关于KMP算法你不知道的事

写在前面：

（阅读本文前需要了解KMP算法的基本思路。另外，本着大道至简的思想，本文的所有例子都会做从头到尾的讲解）

在翻阅了大量网上现有的KMP算法博客后，发现广为流传的竟然是一种不完整的KMP算法。即通过next数组来作为有限状态自动机，以此实现非匹配时的回退。虽然这不失为一种好的方法。

但我想介绍一种更好和更完整的方法————拥有完整DFA的KMP算法

先列出本文要介绍的方法与一般方法对比下的几大优点：

1. 在最坏情况下，对字符串的操作次数仅为一般做法的三分之二。
2. 在所有情况下，对字符串的操作数都小于等于一般做法。
3. 思路上相对于一般做法更加完整细致，学习了它一定能让你对kmp有一个全新的认识。

（读者可以在通读全文之后回头来看这几句话到底对不对）

一、关于有限状态自动机（什么是DFA）

kmp算法模拟了有限状态自动机的运行，一般算法中的next数组和本文中的dfa数组都是作为有限状态自动机的运行指导。

有限状态自动机不同，程序运行起来自然会存在不同。

在本文介绍的KMP算法中，我们使用二维数组DFA来作为有限状态自动机指导：

1. 定义：DFA=new int[R][M],R为文本可能出现的字符种类（EXTENDED_ASCII的R为256位，一般情况下是够用了），M为模式字符串的长度。
2. 空间：DFA占用空间上比next数组大了R倍，但空间的牺牲必然要迎来性能上的提升！
3. 储存内容：和next数组一样的是，DFA也储存了每个位置匹配失败时模式串的重启位置，但它更加详细，DFA针对了匹配失败时可能出现的不同字符对应了其特定的重启位置，这样的好处在后面的性能分析中会降到。

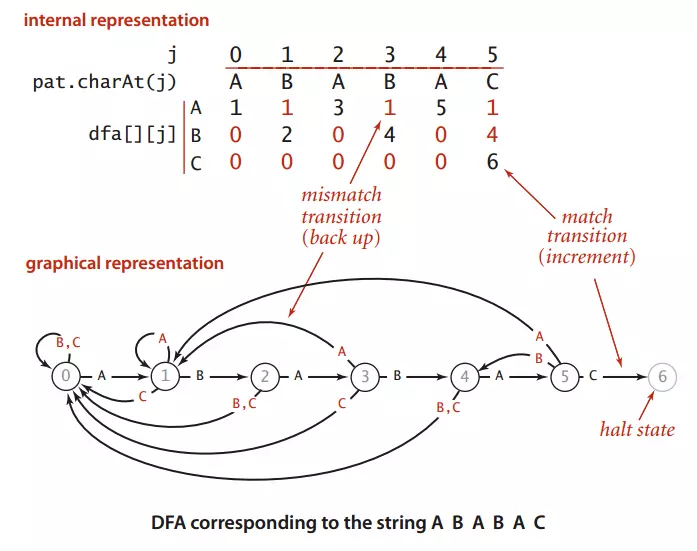
　　　　　　　　　图1　和模式字符串ABABAC对应的确定有限状态机自动机

图一展示了模式字符串pat：ABABAC对应的确定有限状态机自动机

dfa[A][j]表示：模式串成功匹配到第j个位置时文本这时对应字符为'A'的情况下模式串下一个将要匹配的位置。

拿图1来说，dfa[A][3]表示匹配到模式串ABABAC的第三位时（B），文本对应的是A，这时模式串将回到dfa[A][3]=1，也就是将模式串回到ABABAC的第一位（B），然后继续下一位(也是就ABABAC中的第二位,这里是A)与文本的下一位继续比较。

似乎蛮复杂的，但理解了它的构造方法之，你就可以灵活使用它。

1、dfa的构造方法：

我们需要借助j和X来构造dfa，j指向当前的匹配位置，X是匹配失败时的重启位置。一开始j和X都设为0。

对于每个j，我们要做的是：

1. 将daf[][X]复制到daf[][j]（对于匹配失败的情况）
2. 将daf[pat.charAt(j)][j]设为j+1（对于匹配成功的情况）
3. 更新X

用代码表示如下：

（推荐读者先大概看看代码，再结合下面给出的完整例子，然后做代码运行调试）

dfa[pat.charAt(0)][0]=1;
for(int X=0,j=1;j<M;j++){//计算dfa[][j]
    for(int c=0;c<R;c++){//不匹配情况
        dfa[c][j]=dfa[c][X];
    }
    dfa[pat.charAt(j)][j]=j+1;
    X=dfa[pat.charAt(j)][X];
}    

在上面代码的基础上来演示一个完整的构造过程：

① j和X都为0，dfa[pat.charAt(0)][0]=1

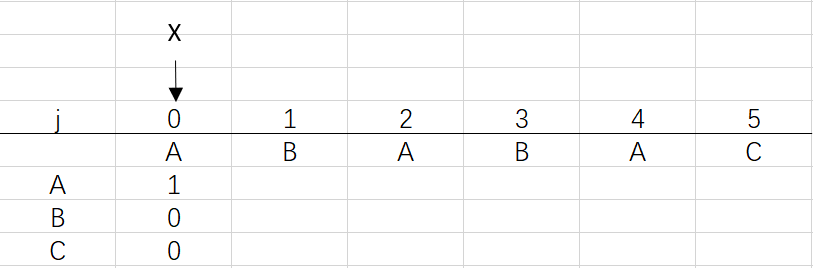
② 进入for循环X=0,j=1：将X的列复制到j的列，再设dfa[pat.charAt(j)][j]=j+1，更新X

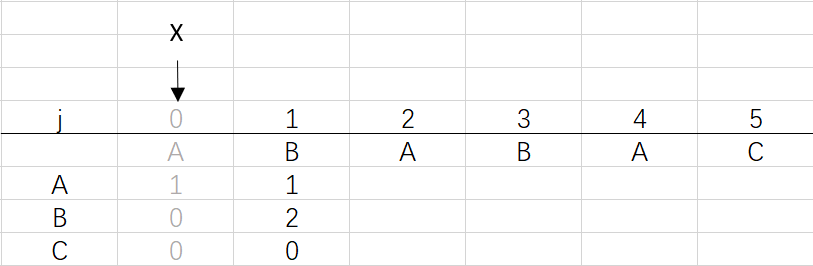
可以看到第三步更新X后X还是0，因为在第二步时X=dfa[pat.charAt(j)][X]=dfa[B][0]=0 （关于X变化的探讨接下来就会提到）

③ 第二次循环X=0,j=2：将X的列复制到j的列，再设dfa[pat.charAt(j)][j]=j+1，更新X

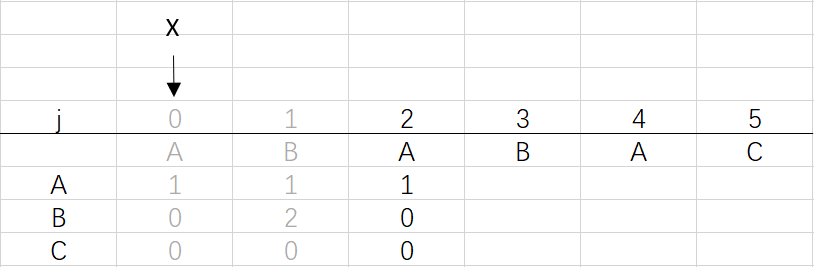
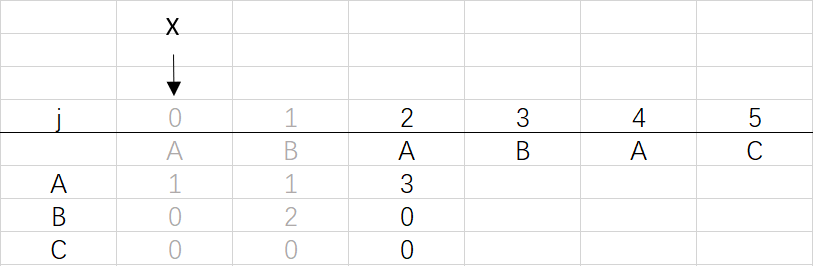
X=dfa[pat.charAt(j)][X]=dfa[A][0]=1

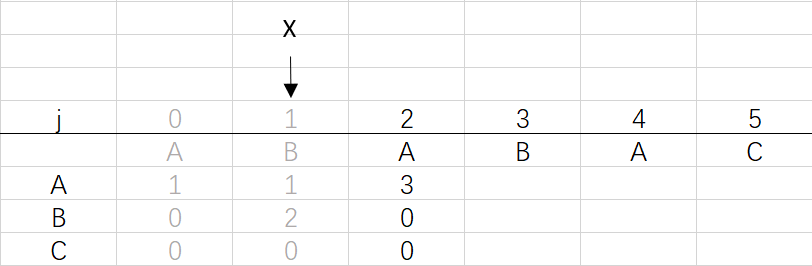
④ 第三次循环X=1,j=3：将X的列复制到j的列，再设dfa[pat.charAt(j)][j]=j+1，更新X

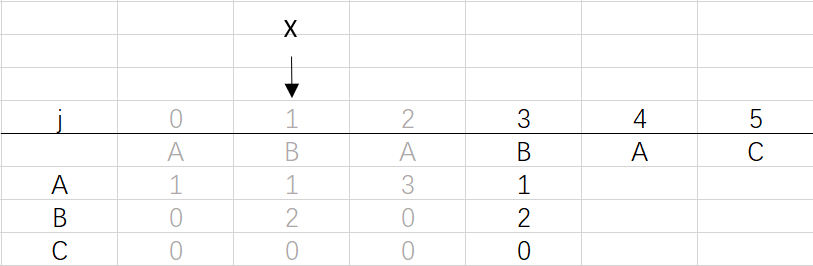
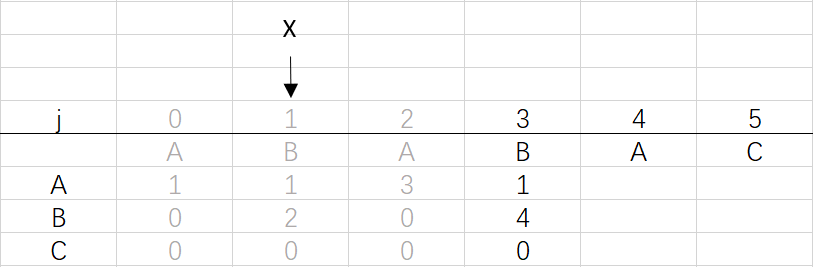
X=dfa[pat.charAt(j)][X]=dfa[B][1]=2

⑤ 第四次循环X=2,j=4：将X的列复制到j的列，再设dfa[pat.charAt(j)][j]=j+1，更新X

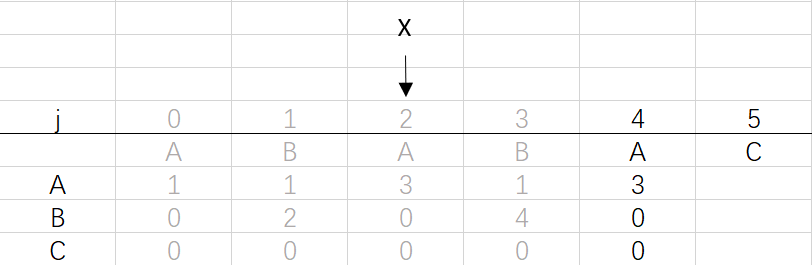
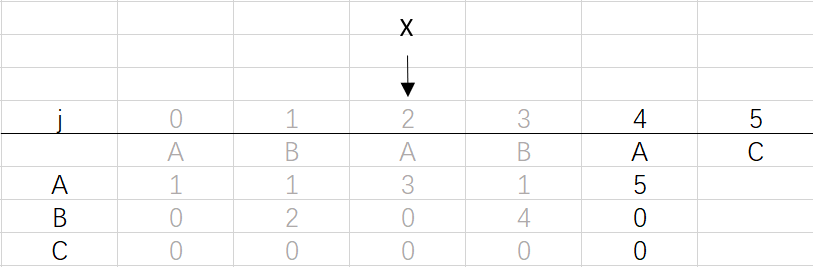
X=dfa[pat.charAt(j)][X]=dfa[A][2]=3

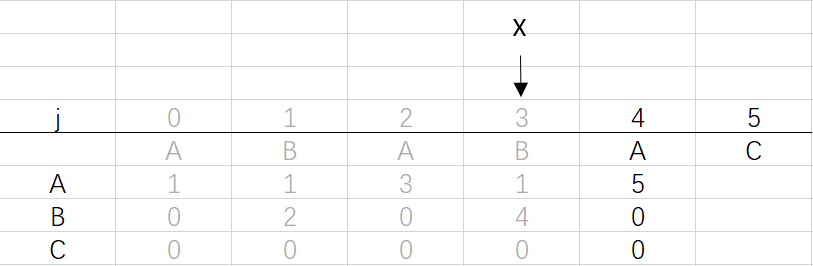
⑥ 第四次循环X=3,j=5：将X的列复制到j的列，再设dfa[pat.charAt(j)][j]=j+1，已经结束到最后一位，不用更新X

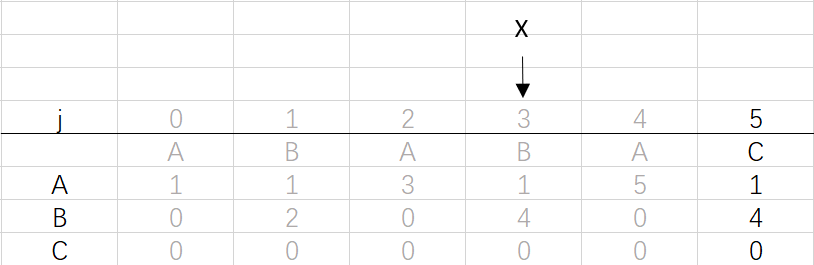
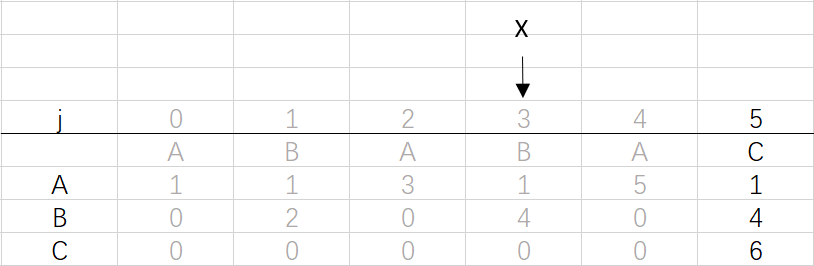
到这里就结束了模式字符串ABABAC的dfa构造最终得到的结果：

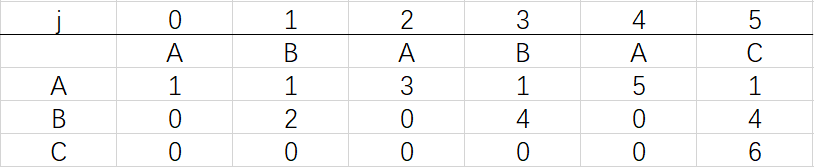
相信大家已经明白了dfa的构造思路

为巩固练习，下面请读者自己构造出模式字符串ABRACAD的daf，然后和下图对照一下是不是一样

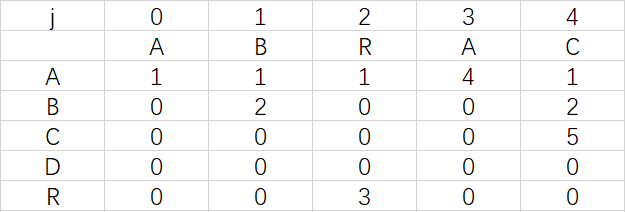
2、关于X的一些问答：

值得一提的是，X是构造dfa的关键，下面几个问答有助于我们理解整个dfa构造。

为什么每次都能得出X的值?

答：因为X永远小于j，X走的是j走的老路。

为什么要把X列复制到j列？

答：dfa里记录了到每种状态时可能的所有选择，如果状态A发生不匹配时可以回到状态B继续匹配，那我们就可以先把状态B复制到状态A，这样在状态A不匹配时就可以直接使用状态B的方案。

X的位置何时会发生变化？

X的下一个位置与j当前指向的字符、j之前指向过的字符、X当前位置都有关，事实上不管j当前指向的字符在之前是否出现过，X都可能移动。

X的位置会怎么变化？

当每次j指向的字符与X指向的字符能够连续对应上的时候，X就会每次向后移一位（字符与前缀对应时X往后移）。

当j指向的字符在之前没有出现过，X就会指向0。

3、实例对问题的证明：

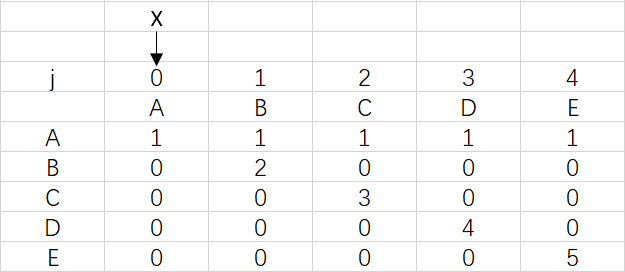
上图是模式ABCDE的dfa数组，可以观察到ABCDE中是没有出现重复字符的，所以到最后X依然指向0

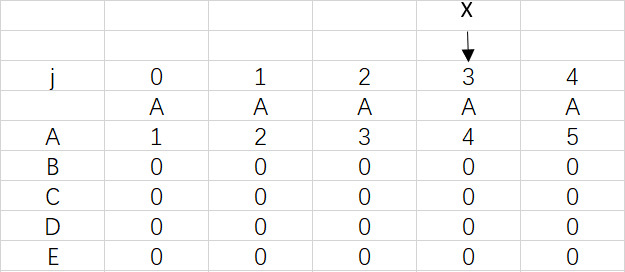
对应极端情况，前面的字符出现重复达到了四次，X也是要移动四次，但只停留在3是因为模式串已经匹配完成，不需要再移动X。

关于X的移动，是需要读者自己在模拟dfa构造中细想的，想明白了就能全懂KMP，不明白就再看看上面的问题，尝试自己作答就会有新的心得。

二、改变搜索方法

有了强大的有限状态自动机，怎么用它呢？实际使用中是否比原来更强大呢？咱直接将两者的代码贴出来一顿对比，顺便说明精妙之处。

大体的思路是一样的，就是将txt字符串从头到尾循环一遍，过程中不断判断模式串的位置

1、先来看看一般方法中的搜索方法代码：

for(i=0;i<n;i++){
    while (j>-1&&txt.charAt(i)!=pat.charAt(j)){
        j=next[j];
    }
    if(j==-1||txt.charAt(i)==pat.charAt(j)){
        j++;
    }
    if(j==m){return i-j;
    }
}            

一边从头到尾循环，一边判断j是不是等于m，应该注意到的是，for循环中还包含了一个while，用来做回退和继续匹配的。

可以发现，这个过程中的操作次数必定是要大于i的（每次for循环都可能要加入while）

2、下面是使用dfa后的搜索方法：

for(j=0,i=0;i<N&&j<M;i++){
    j=dfa[txt.charAt(i)][j];
}
if(j==M){
    System.out.println("匹配成功");
    return i-M;
}else {
    System.out.println("匹配失败");
    return N;
}

可以看到，在for循环之后，直接进行匹配成功或失败的判断，整个过程的操作次数等于i，是小于一般方法的。

三、性能分析对比

①当字符串不匹配时（这是两种方法差异最大的地方）：

使用DFA二维数组作为有限状态自动机，每次不匹配时都能到达精准位置（对每个不匹配的情况dfa都有记录在案）。

而使用next一维数组时，在每次匹配失败后到达的位置是不能确认的，它只是先到达可能的位置。

从可能的最长前缀位置，进行字符的匹配，如果不匹配再移到下一位可能的位置（下标在模式字符串上往前移）。

②当字符串匹配时

在两种方式中是一样的，i和j都加一，然后进入下一个for循环。

②最坏情况什么时候出现

对于一般方法：如果文本为AAAA,模式串为AAAB，这时匹配到最后一位时失败，j会一步步往前走，这时在搜索方法中操作次数达到了2n，加上构造next数组的n次操作，共3n次操作。

对于完整KMP算法：上面的情况并不会使它达到3n，因为在j一步步往前走的时候i也会往后走，当i达到n时for循环结束，这样最多也就操作n次，加上dfa数组的构造需要n次，共2n次操作。

结果：

可以看到，在通常情况下完整KMP算法的操作次数要比一般算法的操作次数少

即便是在最坏情况下完整KMP算法的操作次数也为一般方法的三分之二。

足以证明完整KMP的性能是更优的。

四、完整实现及测试代码（java）

 public class KMP {
     private String pat;
     private int dfa[][];

     public KMP(String pat){//由模式字符串构建dfa
         this.pat=pat;
         int M=pat.length();
         int R=256;
         dfa=new int[R][M];
         dfa[pat.charAt(0)][0]=1;
         for(int X=0,j=1;j<M;j++){//计算dfa[][j]
             for(int c=0;c<R;c++){//不匹配情况
                 dfa[c][j]=dfa[c][X];
             }
             dfa[pat.charAt(j)][j]=j+1;
             X=dfa[pat.charAt(j)][X];
         }
     }

     public int search(String txt){
         int N= txt.length();
         int M=pat.length();
         int j,i;
         for(j=0,i=0;i<N&&j<M;i++){
             j=dfa[txt.charAt(i)][j];
         }
         if(j==M){
             System.out.println("匹配成功");
             return i-M;
         }else {
             System.out.println("匹配失败");
             return N;
         }
     }
 }

测试例子：

     @Test
     public void KMPTest(){
         KMP kmp=new KMP("abc");
         System.out.println(kmp.search("abfeabcabc"));
     }