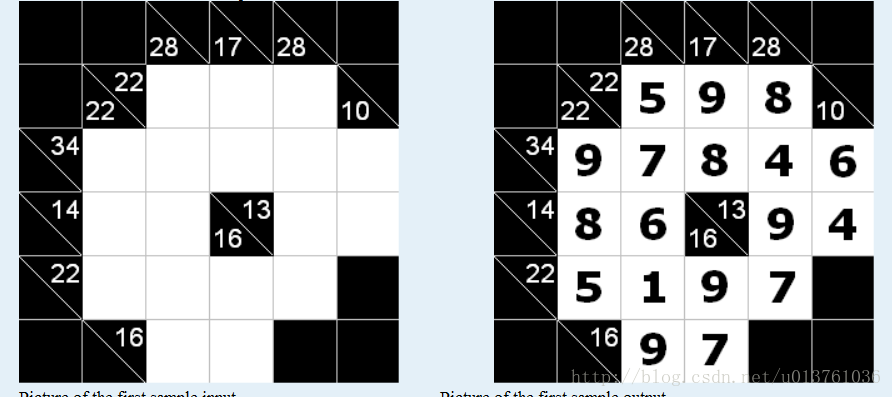
hdu3338 最大流

题意: 

           给你一个N*M的网格,上面有的有一些数字,要求填充数字,满足的规则是这样:

答案不唯一,只要满足和的关系就可以,还有就是只能用1--9之间的数字填充,而且每一行或一列可以重复使用某个数字,观察每个要填充的点我们会发现,其实该点只于他所在的"行和"限制和所在的"列和"限制,我们可以把点分为三类,白色填充,左下半有数,右下半

有数 ,(其他的没用,不用管 ,左下和右上都有数的一定要拆成两个点),只要权衡好这三类点就ok了,那么我们可以直接添加 超级远点s ,超级汇点e ,左下进右上出(也可以反过来);题目要求是1--9 ,最大流可能会产生0所以直接0--8,输出的时候在+1就行.题意既然说是保证有解,那么最大流肯定会满流,最后每个点流多少就输出多少+1就ok;

建图:

(1)s 和所有左下有数的点连 ,流量是左下的数字减去他下面空白行的个数(因为是0--8每个都少了1 ,一共有多少个就少多少个)

(2)所有左下角有数的点和他下面的这一列的空白点相连,流量 8

(3)所有右上角有数的被他所在的这一列空白的连接,记住是被连接,(方向别反了),还有注意一点就是如果该点左下角有数了,那么一定要拆点,不然会冲突,流量是8;

(4)第三步中所有被连接的点在连接e,流量是该点右上角的数 - 这一行的空白格子个数.原因和(1) 一样.

      建图后直接一遍最大流,然后根据流量情况就能输出答案了, 题目是 Special Judge ..所以随便跑一遍就行了,还有就是别用DINIC,会超时,就算我把点都离散化了依然超时,我用的是

SAP之前没用过,随便找了个模板改改用的. 当某个点有两个值时一定要拆点.同时可以离散化去优化.  

下面是代码,第一个是TLE代码(DINIC),第二个是AC代码(SAP);

// 超时的DINIC

#include<stdio.h>

#include<string.h>

#include<queue>

#define N_node 100 * 100 * 2 + 100

#define N_edge 500000

#define N 100 + 5

#define inf 1000000000

using namespace std;

typedef struct

{

   char node[8];

}NODE;

typedef struct

{

   int to ,next ,cost;

}STAR;

typedef struct

{

   int x ,dep;

}DEP;

NODE map[N][N];

STAR E[N_edge]; 

DEP xin ,tou;

int list[N_node] ,tot;

int list2[N_node] ,deep[N_node];

int X[N*N*2+100];

void add(int a ,int b ,int c)

{

   E[++tot].to = b;

   E[tot].cost = c;

   E[tot].next = list[a];

   list[a] = tot;

   

   E[++tot].to = a;

   E[tot].cost = 0;

   E[tot].next = list[b];

   list[b] = tot;

}

int minn(int x ,int y)

{

   return x < y ? x : y;

}

bool BFS_DEEP(int s ,int t ,int n)

{

   memset(deep ,255 ,sizeof(deep));

   deep[s] = 0;

   xin.x = s ,xin.dep = 0;

   queue<DEP>q;

   q.push(xin);

   while(!q.empty())

   {

      tou = q.front();

      q.pop();

      for(int k = list[tou.x] ;k ;k = E[k].next)

      {

         xin.x = E[k].to;

         xin.dep = tou.dep + 1;

         if(deep[xin.x] != -1 || !E[k].cost)

         continue;

         deep[xin.x] = xin.dep;

         q.push(xin);

      }

   }

   for(int i = 0 ;i <= n ;i ++)

   list2[i] = list[i];

   return deep[t] != -1;

}

int DFS_FLOW(int s ,int t ,int flow)

{

   if(s == t) return flow;        

   int nowflow = 0;

   for(int k = list2[s] ;k ;k = E[k].next)

   {

      list2[s] = k;

      int to = E[k].to;

      int c = E[k].cost;

      if(deep[to] != deep[s] + 1 || !c)

      continue;

      int temp = DFS_FLOW(to ,t ,minn(c ,flow - nowflow));

      nowflow += temp;

      E[k].cost -= temp;

      E[k^1].cost += temp;

      if(nowflow == flow) break;

   }

   if(!nowflow) deep[s] = 0;

   return nowflow;

}

int DINIC(int s ,int t ,int n)

{

   int ans = 0;

   while(BFS_DEEP(s ,t ,n))

   {        

      ans += DFS_FLOW(s ,t ,inf);

   }

   return ans;

}

int main ()

{

   int i ,j ,n ,m ,s ,e;

   while(~scanf("%d %d" ,&n ,&m))

   {

      int sum_n = 0;

      for(i = 1 ;i <= n ;i ++)

      for(j = 1 ;j <= m ;j ++)

      {

         scanf("%s" ,map[i][j].node);

         if(map[i][j].node[0] == '.')

         {

            sum_n ++;

            continue;

         }

         if(map[i][j].node[0] != 'X')

         sum_n ++;

         if(map[i][j].node[4] != 'X')

         sum_n ++;

      }

          

      s = 0 ,e = sum_n + 1;

      sum_n = 0;

      memset(X ,255 ,sizeof(X));                      

      memset(list ,0 ,sizeof(list)) ,tot = 1;

      for(i = 1 ;i <= n ;i ++)

      for(j = 1 ;j <= m ;j ++)

      {

         if(map[i][j].node[3] == 'X' || map[i][j].node[0] == '.') continue;

         char t_str[8];

         for(int ii = 0 ;ii <= 7 ;ii ++)

         t_str[ii] = map[i][j].node[ii];

         int a ,b ,mk = 0;

         if(X[(i-1)*m+j] == -1) X[(i-1)*m+j] = ++sum_n;

         int now =  X[(i-1)*m+j];

         if(t_str[0] != 'X')

         {

            mk = 1;

            int temp = (t_str[0]-48)*100+(t_str[1]-48)*10+(t_str[2]-48)*1; 

            for(int ii = i + 1 ;ii <= n ;ii ++)

            {

               if(map[ii][j].node[0] != '.')

               break;

               temp --;

               if(X[(ii - 1) * m + j] == -1) X[(ii - 1) * m + j] = ++sum_n;

               b = X[(ii - 1) * m + j];       

               add(now ,b ,8);

            }

            add(s ,now ,temp);

         }

         

         if(t_str[4] != 'X')

         {                    

            if(mk) now = ++sum_n;

            int temp = (t_str[4]-48)*100+(t_str[5]-48)*10+(t_str[6]-48)*1;

            for(int jj = j + 1 ;jj <= m ;jj ++)

            {

               if(map[i][jj].node[0] != '.')

               break;

               temp --;

               if(X[(i - 1) * m + jj] == -1) X[(i - 1) * m + jj] = ++sum_n;

               a = X[(i - 1) * m + jj];

               add(a ,now ,8);

            }

            add(now ,e ,temp);

         }

      }

      

      DINIC(s ,e ,sum_n + 1);

      for(i = 1 ;i <= n ;i ++)

      for(j = 1 ;j <= m ;j ++)

      {

         if(j != 1) printf(" ");

         if(map[i][j].node[0] != '.')

         printf("_");

         else

         {

            int k = list[X[(i - 1) * m + j]];

            int c = E[k].cost;

            printf("%d" ,8 - c + 1);

         }

         if(j == m) printf("\n");

      }

   }

   return 0;

}
  

//SAP ac

#include<stdio.h>

#include<string.h>

#include<queue>

#define N 100 + 5

using namespace std;

typedef struct

{

   char node[8];

}NODE;

NODE map[N][N];

int X[50000];

//***********************************************

const int MAXN=50000;//点数的最大值

const int MAXM=1000000;//边数的最大值

const int INF=0x3f3f3f3f;

struct Node

{

    int from,to,next;

    int cap;

}edge[MAXM];

int tol;

int head[MAXN];

int dep[MAXN];

int gap[MAXN];//gap[x]=y :说明残留网络中dep[i]==x的个数为y

int nn;//n是总的点的个数，包括源点和汇点

void init()

{

    tol=0;

    memset(head,-1,sizeof(head));

}

void addedge(int u,int v,int w)

{

    edge[tol].from=u;

    edge[tol].to=v;

    edge[tol].cap=w;

    edge[tol].next=head[u];

    head[u]=tol++;

    edge[tol].from=v;

    edge[tol].to=u;

    edge[tol].cap=0;

    edge[tol].next=head[v];

    head[v]=tol++;

}

void BFS(int start,int end)

{

    memset(dep,-1,sizeof(dep));

    memset(gap,0,sizeof(gap));

    gap[0]=1;

    int que[MAXN];

    int front,rear;

    front=rear=0;

    dep[end]=0;

    que[rear++]=end;

    while(front!=rear)

    {

        int u=que[front++];

        if(front==MAXN)front=0;

        for(int i=head[u];i!=-1;i=edge[i].next)

        {

            int v=edge[i].to;

            if(dep[v]!=-1)continue;

            que[rear++]=v;

            if(rear==MAXN)rear=0;

            dep[v]=dep[u]+1;

            ++gap[dep[v]];

        }

    }

}

int SAP(int start,int end)

{

    int res=0;

    BFS(start,end);

    int cur[MAXN];

    int S[MAXN];

    int top=0;

    memcpy(cur,head,sizeof(head));

    int u=start;

    int i;

    while(dep[start]<nn)

    {

        if(u==end)

        {

            int temp=INF;

            int inser;

            for(i=0;i<top;i++)

               if(temp>edge[S[i]].cap)

               {

                   temp=edge[S[i]].cap;

                   inser=i;

               }

            for(i=0;i<top;i++)

            {

                edge[S[i]].cap-=temp;

                edge[S[i]^1].cap+=temp;

            }

            res+=temp;

            top=inser;

            u=edge[S[top]].from;

        }

        if(u!=end&&gap[dep[u]-1]==0)//出现断层，无增广路

          break;

        for(i=cur[u];i!=-1;i=edge[i].next)

           if(edge[i].cap!=0&&dep[u]==dep[edge[i].to]+1)

             break;

        if(i!=-1)

        {

            cur[u]=i;

            S[top++]=i;

            u=edge[i].to;

        }

        else

        {

            int min=nn;

            for(i=head[u];i!=-1;i=edge[i].next)

            {

                if(edge[i].cap==0)continue;

                if(min>dep[edge[i].to])

                {

                    min=dep[edge[i].to];

                    cur[u]=i;

                }

            }

            --gap[dep[u]];

            dep[u]=min+1;

            ++gap[dep[u]];

            if(u!=start)u=edge[S[--top]].from;

        }

    }

    return res;

}

//**************************************

int main ()

{

   int i ,j ,n ,m ,s ,e;

   while(~scanf("%d %d" ,&n ,&m))

   {

      int sum_n = 0;

      for(i = 1 ;i <= n ;i ++)

      for(j = 1 ;j <= m ;j ++)

      {

         scanf("%s" ,map[i][j].node);

         if(map[i][j].node[0] == '.')

         {

            sum_n ++;

            continue;

         }

         if(map[i][j].node[0] != 'X')

         sum_n ++;

         if(map[i][j].node[4] != 'X')

         sum_n ++;

      }

         

      s = 0 ,e = sum_n + 1;

      sum_n = 0;

      memset(X ,255 ,sizeof(X));                      

      memset(head ,255 ,sizeof(head));

      tol = 0;

      for(i = 1 ;i <= n ;i ++)

      for(j = 1 ;j <= m ;j ++)

      {

         if(map[i][j].node[3] == 'X' || map[i][j].node[0] == '.') continue;

         char t_str[8];

         for(int ii = 0 ;ii <= 7 ;ii ++)

         t_str[ii] = map[i][j].node[ii];

         int a ,b ,mk = 0;

         if(X[(i-1)*m+j] == -1) X[(i-1)*m+j] = ++sum_n;

         int now =  X[(i-1)*m+j];

         if(t_str[0] != 'X')

         {

            mk = 1;

            int temp = (t_str[0]-48)*100+(t_str[1]-48)*10+(t_str[2]-48)*1; 

            for(int ii = i + 1 ;ii <= n ;ii ++)

            {

               if(map[ii][j].node[0] != '.')

               break;

               temp --;

               if(X[(ii - 1) * m + j] == -1) X[(ii - 1) * m + j] = ++sum_n;

               b = X[(ii - 1) * m + j];       

               addedge(now ,b ,8);

            }

            addedge(s ,now ,temp);

         }

         

         if(t_str[4] != 'X')

         {                    

            if(mk) now = ++sum_n;

            int temp = (t_str[4]-48)*100+(t_str[5]-48)*10+(t_str[6]-48)*1;

            for(int jj = j + 1 ;jj <= m ;jj ++)

            {

               if(map[i][jj].node[0] != '.')

               break;

               temp --;

               if(X[(i - 1) * m + jj] == -1) X[(i - 1) * m + jj] = ++sum_n;

               a = X[(i - 1) * m + jj];

               addedge(a ,now ,8);

            }

            addedge(now ,e ,temp);

         }

      }

      

      nn = sum_n + 1 + 1;

      SAP(s ,e);

      for(i = 1 ;i <= n ;i ++)

      for(j = 1 ;j <= m ;j ++)

      {

         if(j != 1) printf(" ");

         if(map[i][j].node[0] != '.')

         printf("_");

         else

         {

            int k = head[X[(i - 1) * m + j]];

            int c = edge[k].cap;

            printf("%d" ,8 - c + 1);

         }

         if(j == m) printf("\n");

      }

   }

   return 0;

}